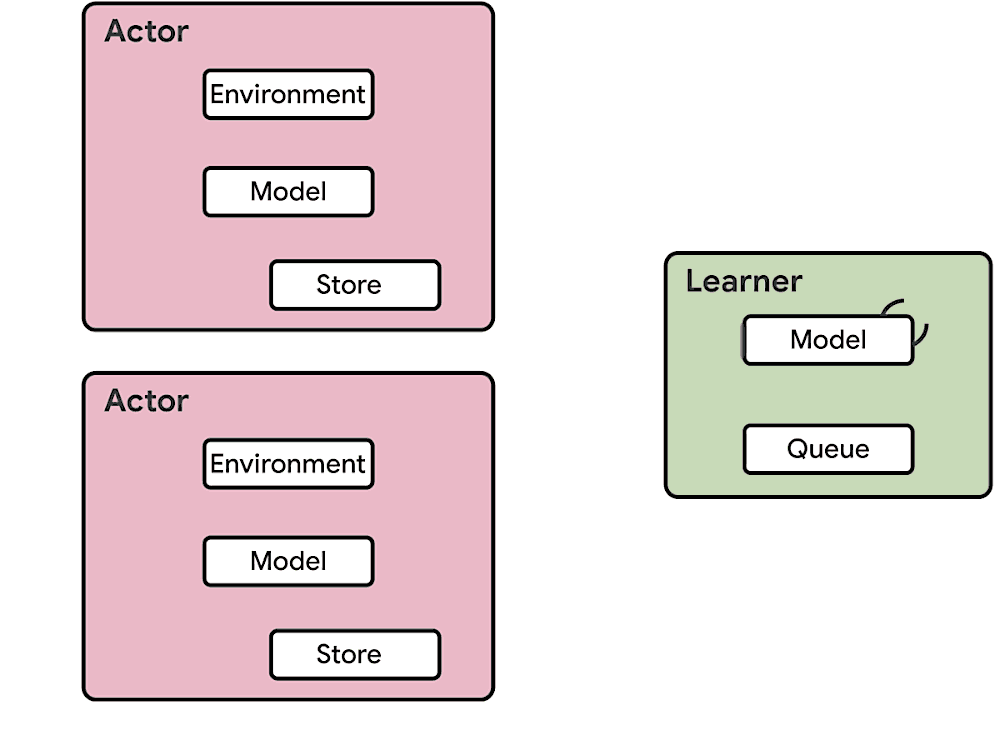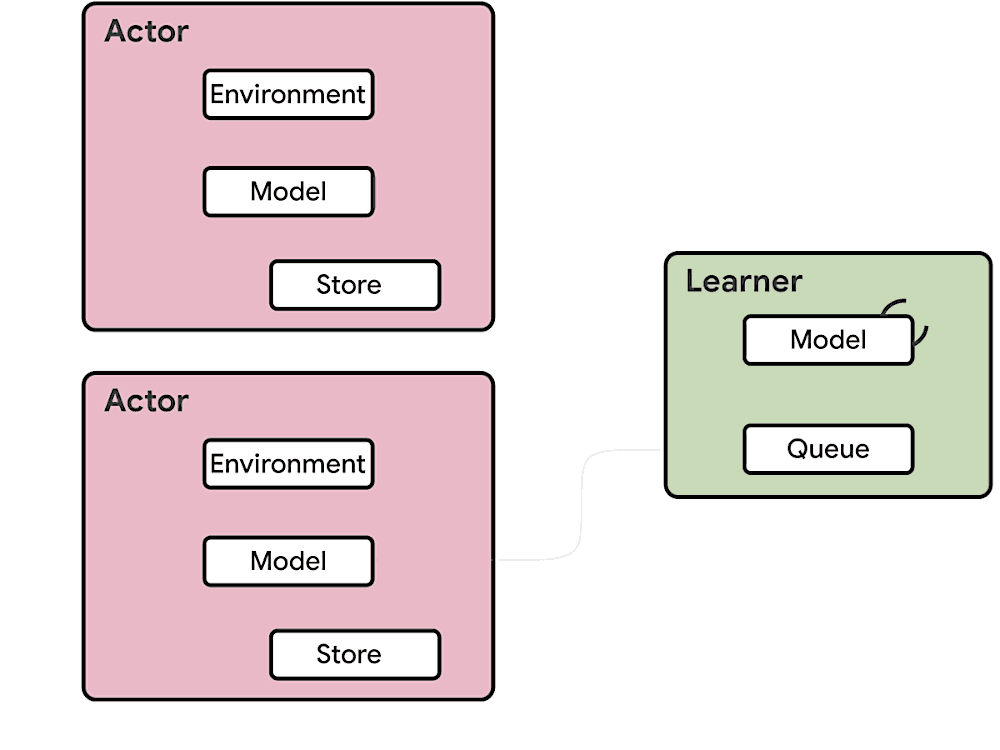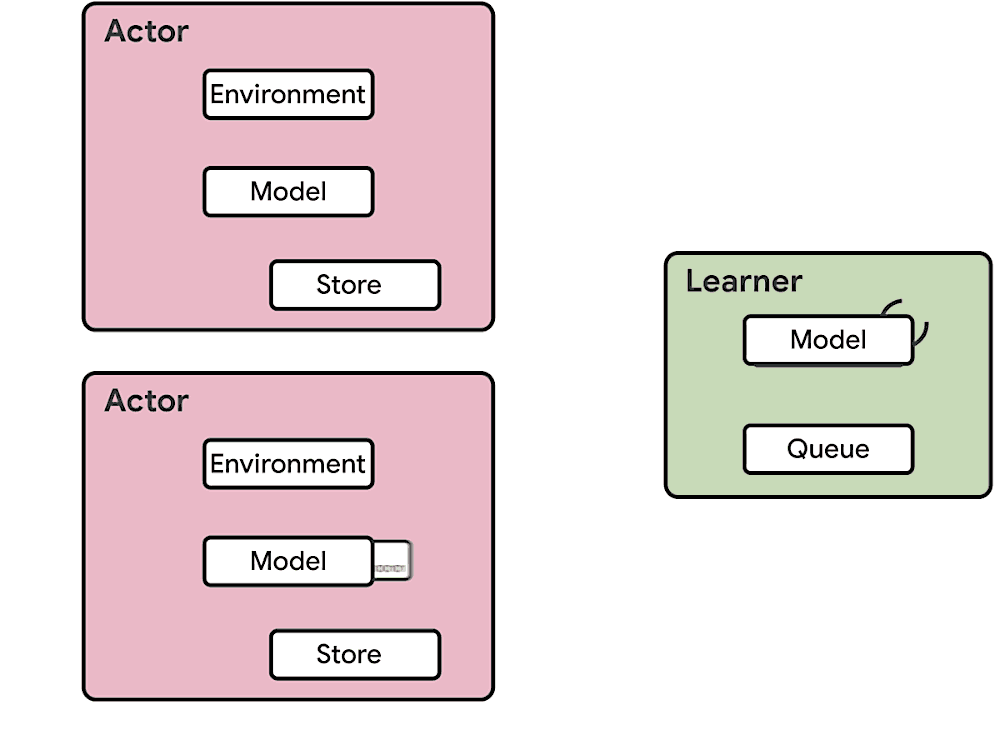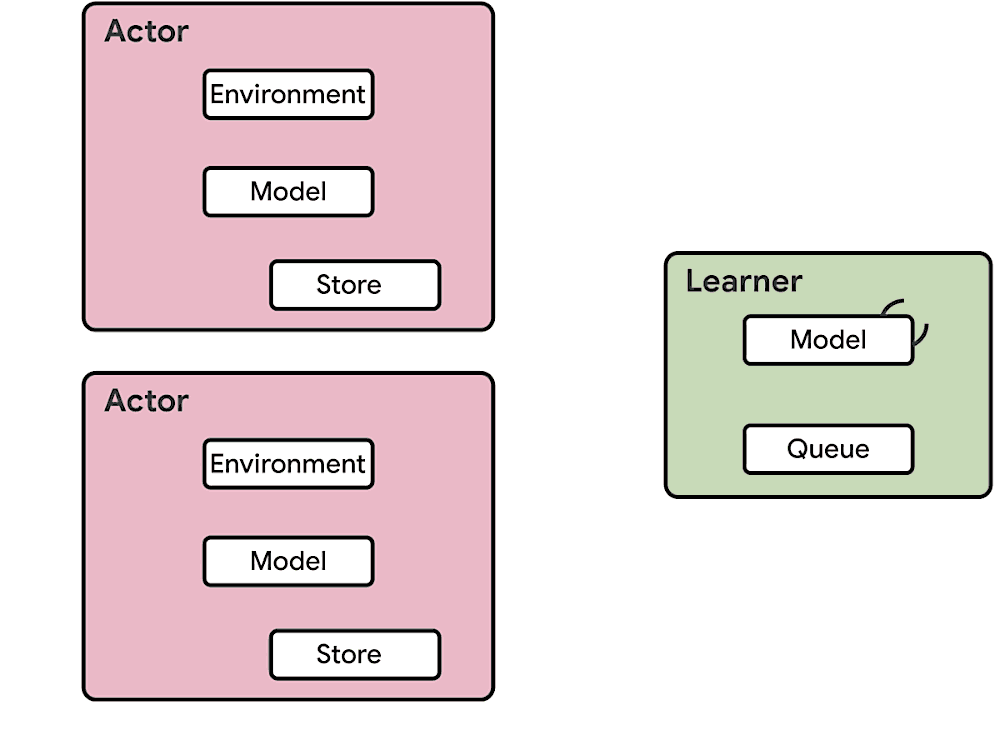
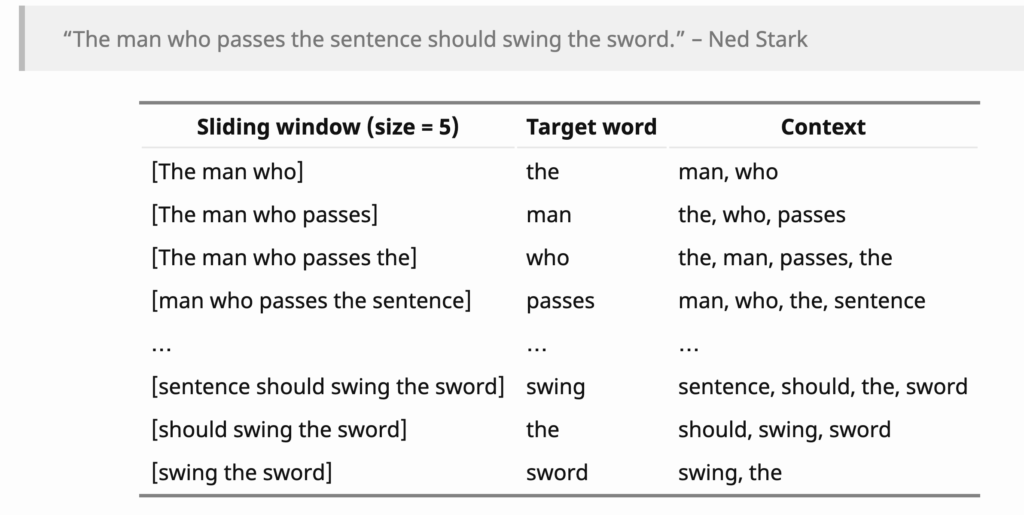
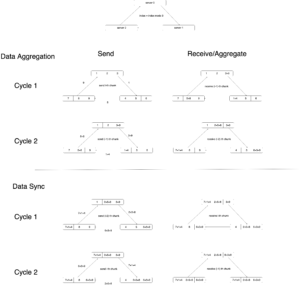
DistributedDataParallel implements data parallelism at the module level which can run across different machines. There is one process running on each device where one copy of the module is held. Each process loads its own data which is non-overlapping with other processes’. At the initialization phase, all copies are synchronized to ensure they start from the same initialized weights. The forward pass is executed independently on each device, during which no communication is needed. In the backward pass, the gradients are all-reduced across the devices, ensuring that each device ends up with identical copy of the gradients/weights, therefore eliminating the need for model syncs at the beginning of each iteration [1].
[2] illustrates some more detailed design. For example, parameters can be synchronized more efficiently by bucketing. Parameters will be bucketed into several buckets. In the backward phase, whenever the gradient is ready for all the members in a bucket, the synchronization will kick off for that bucket. Thus one does not need to wait for the gradients of ALL parameters to become ready before synchronization starts.
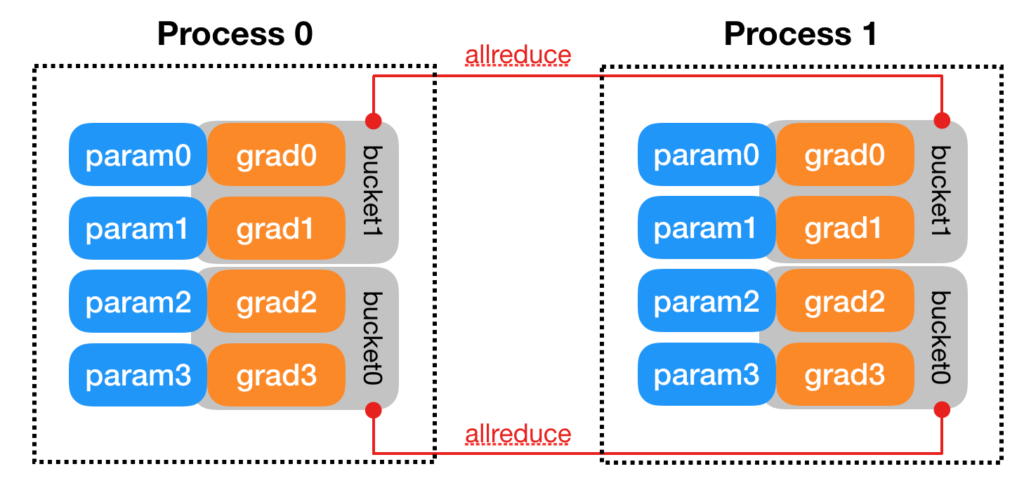
Another detail in [2] is how gradient synchronization is started in the backward phase. It says that “DDP uses autograd hooks registered at construction time to trigger gradients synchronizations. “
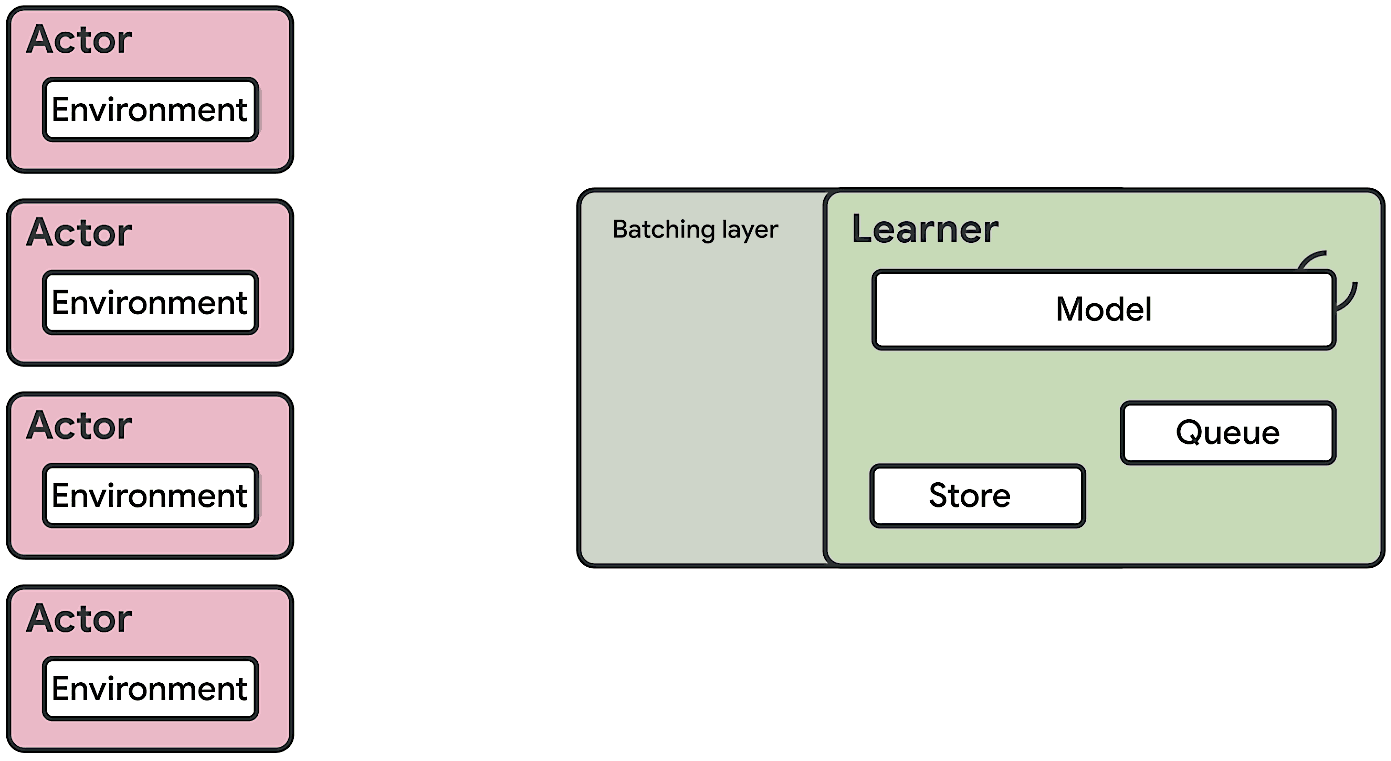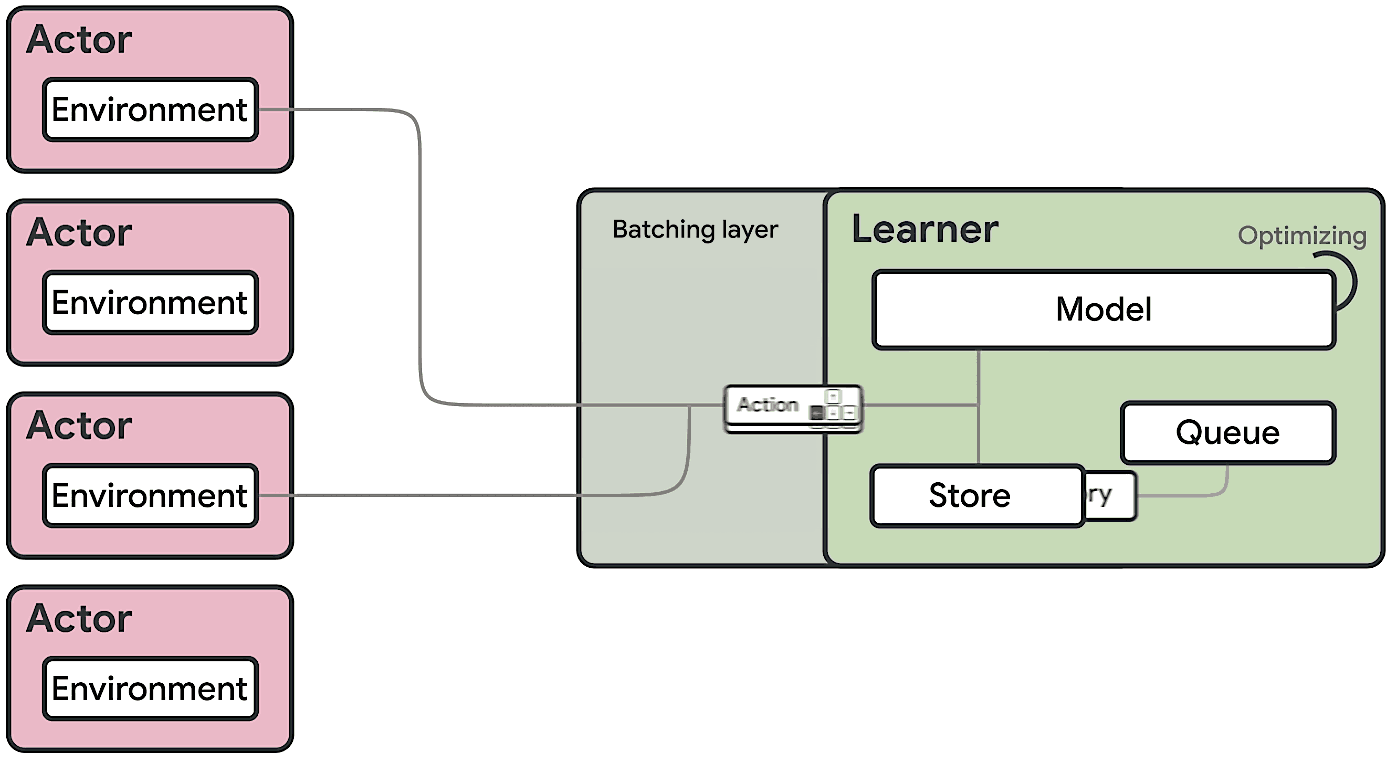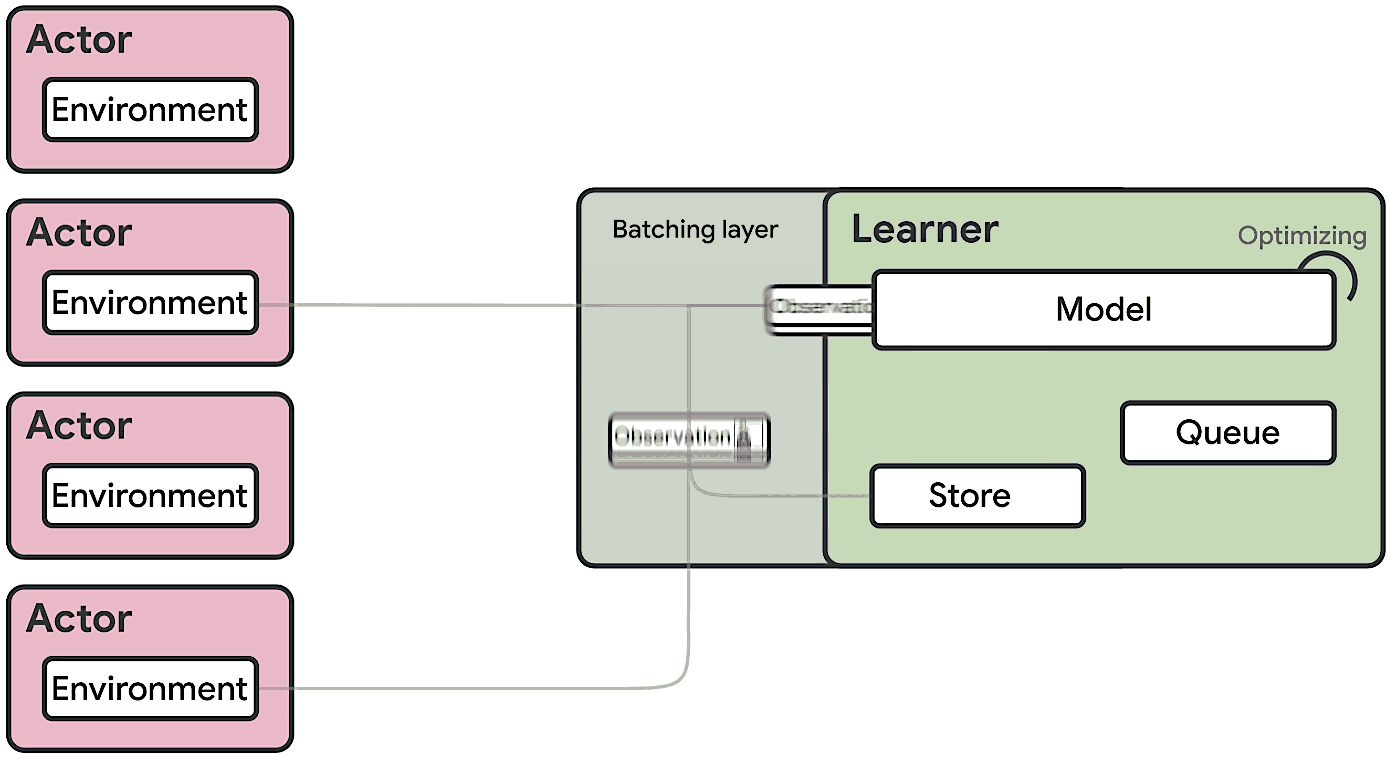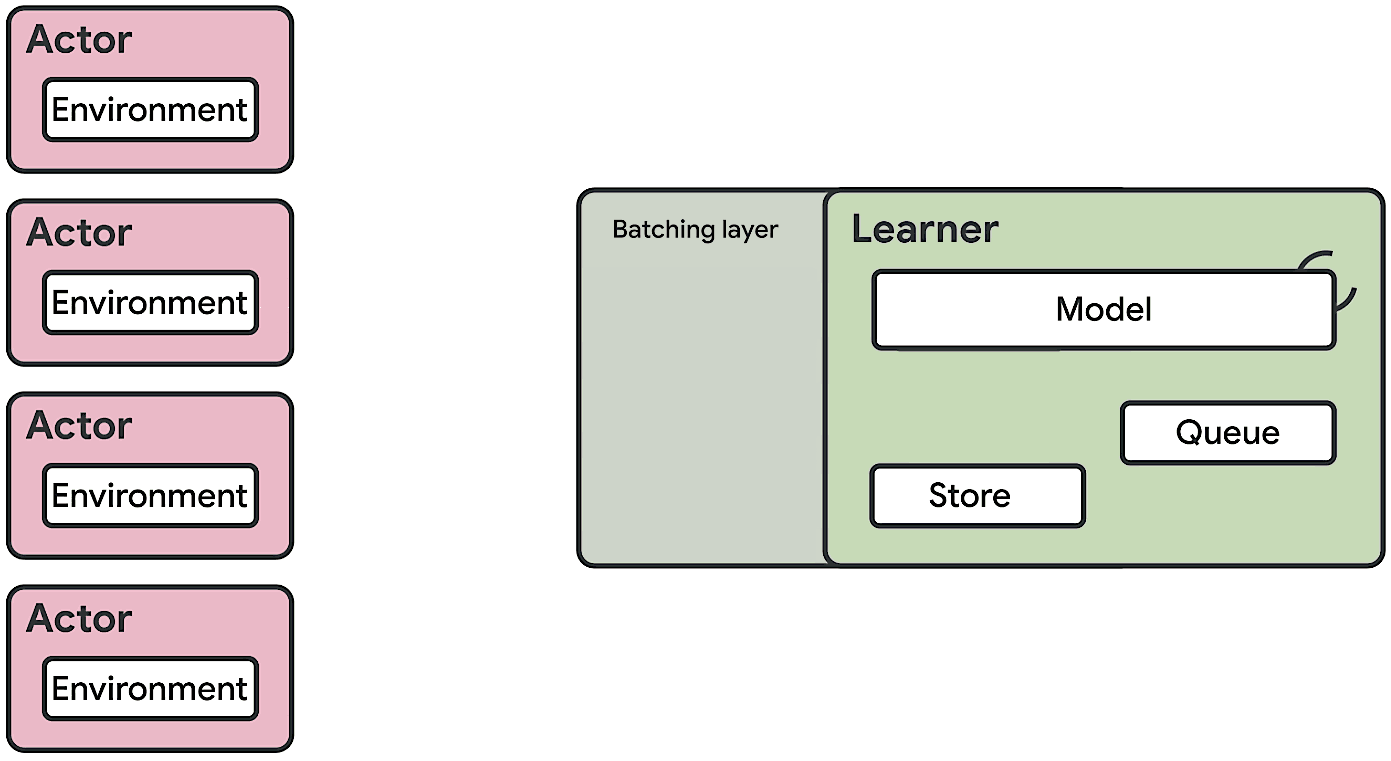
I did a quick experiment to verify these design details. test_multi_gpu is in charge of spawning worker processes and the real model training happens in the _worker function. initialize_trainer is the piece of code for initializing models at each process. Check out my comment in “Logs” section in the pseudocode below for the explanation for DPP’s behavior.
def test_multi_gpu(
use_gpu: bool,
num_gpus: int,
normalization_data_map: Dict[str, NormalizationData],
reader_options: ReaderOptions,
):
logger.info(f"Enter test_multi_gpu with reader options {reader_options}")
# These ENVS are needed by torch.distributed: https://fburl.com/1i86h2yg
os.environ["MASTER_ADDR"] = "127.0.0.1"
os.environ["MASTER_PORT"] = str(find_unused_port())
manager = mp.Manager()
result_dict = manager.dict()
workflow_run_id = flow.get_flow_environ().workflow_run_id
# The second condition is to avoid collision in unit test.
# When running unit test, a local DB is used.
# As a result, the workflow run ID may not be unique.
if workflow_run_id and workflow_run_id > 10000:
init_method = f"zeus://{workflow_run_id}"
else:
host_name = socket.gethostname()
process_id = os.getpid()
init_method = f"zeus://{host_name}_{process_id}"
backend = "nccl" if use_gpu else "gloo"
mp.spawn(
_worker,
args=(
use_gpu,
num_gpus,
backend,
init_method,
reader_options,
normalization_data_map,
result_dict,
),
nprocs=num_gpus,
join=True,
)
logger.info("finish spawn")
def _worker(
rank: int,
use_gpu: bool,
world_size: int,
backend: str,
init_method: str,
reader_options: ReaderOptions,
normalization_data_map: Dict[str, NormalizationData],
reward_options: Optional[RewardOptions] = None,
warmstart_path: Optional[str] = None,
output_dict=None,
):
logger.info(f"rank={rank} with reader options {reader_options}")
dist.init_process_group(
backend=backend, init_method=init_method, world_size=world_size, rank=rank
)
if use_gpu:
torch.cuda.set_device(rank)
model = create_model(...)
trainer = model.initialize_trainer(
use_gpu=use_gpu,
reward_options=reward_options,
normalization_data_map=normalization_data_map,
warmstart_path=warmstart_path,
)
logger.info(f"rank={rank} finish initialize")
num_of_data = 0
data_reader = construct_distributed_data_reader(
normalization_data_map, reader_options
)
for idx, batch in enumerate(data_reader):
batch = post_data_loader_preprocessor(batch)
if use_gpu:
batch = batch.cuda()
num_of_data += len(batch.training_input.state.float_features)
logger.info(
f"rank={rank} batch state={batch.training_input.state.float_features}"
)
logger.info(
f"rank={rank} before train seq2slate param={print_param(trainer.seq2slate_net.seq2slate_net.seq2slate)}"
)
if rank == 1:
logger.info(f"rank={rank} wake")
time.sleep(60)
logger.info(f"rank={rank} sleep")
trainer.train(batch)
logger.info(
f"rank={rank} after train seq2slate param={print_param(trainer.seq2slate_net.seq2slate_net.seq2slate)}"
)
break
logger.info(f"rank={rank} finish reading {num_of_data} data")
def initialize_trainer(self) -> Seq2SlateTrainer:
seq2slate_net = initialize_model(...)
if self.use_gpu:
seq2slate_net = seq2slate_net.cuda()
logger.info(f"Within manager {print_param(seq2slate_net.seq2slate)}")
logger.info(
f"Within manager {next(seq2slate_net.seq2slate.parameters()).device}"
)
if self.trainer_param.num_parallel > 1:
seq2slate_net = _DistributedSeq2SlateNet(seq2slate_net)
return _initialize_trainer(seq2slate_net)
###############
Logs
###############
# This is printed within manager.initialize_trainer to show that
# models are initially with different parameters
# (see line 66 then line 112~115):
I1003 063214.340 seq2slate_transformer.py:140] Within manager tensor([-0.2585, 0.3716, -0.1077, -0.2114, 0.1636, 0.1398, -0.2960, -0.1204,\n ...], device='cuda:0', grad_fn=<CatBackward>)
I1003 063214.341 seq2slate_transformer.py:142] Within manager cuda:0
I1003 063214.349 seq2slate_transformer.py:140] Within manager tensor([-0.1076, -0.0444, 0.3003, -0.1177, 0.0275, -0.0811, 0.2084, 0.3369,\n ...], device='cuda:1', grad_fn=<CatBackward>)
# Below is printed from line 85 ~ 90
# You can see that each process receives different, non-overlapping data
# You can also see that at this point, the two models have the same parameters,
# which are ensured by DDP. The parameters come from one particular copy (rank=0)
I1003 063214.531 test_multi_gpu.py:144] rank=0 batch state=tensor([[ 0.0000, 0.0000, -0.0000, ..., -1.6131, -1.6298, -1.6118],\n ...]],\n device='cuda:0')
I1003 063214.540 test_multi_gpu.py:147] rank=0 before train seq2slate param=tensor([-0.2585, 0.3716, -0.1077, -0.2114, 0.1636, 0.1398, -0.2960, -0.1204,\n
...], device='cuda:0', grad_fn=<CatBackward>)
I1003 063214.544 test_multi_gpu.py:144] rank=1 batch state=tensor([[ 0.0000, 0.0000, -0.7115, ..., -2.2678, -2.3524, -2.4194],\n ...]],\n device='cuda:1')
I1003 063214.553 test_multi_gpu.py:147] rank=1 before train seq2slate param=tensor([-0.2585, 0.3716, -0.1077, -0.2114, 0.1636, 0.1398, -0.2960, -0.1204,\n ..., device='cuda:1', grad_fn=<CatBackward>)
# We deliberately let rank 1 sleep for one minute.
# But you can see that rank 0 does not return from its train function earlier
# because it blocks on .backward function, waiting for rank 1's backward() finish.
# You can see after .train function, both processes have resulted to the same parameters again
I1003 063214.554 test_multi_gpu.py:150] rank=1 wake
I1003 063314.613 test_multi_gpu.py:152] rank=1 sleep
I1003 063315.023 seq2slate_trainer.py:181] 1 batch: ips_loss=-2.706389904022217, clamped_ips_loss=-2.706389904022217, baseline_loss=0.0, max_ips=27.303083419799805, mean_ips=0.6373803615570068, grad_update=True
I1003 063315.033 test_multi_gpu.py:156] rank=0 after train seq2slate param=tensor([-0.2485, 0.3616, -0.0977, -0.2214, 0.1736, 0.1298, -0.3060, -0.1304,\n ...], device='cuda:0', grad_fn=<CatBackward>)
I1003 063315.033 test_multi_gpu.py:161] rank=0 finish reading 1024 data
I1003 063315.039 seq2slate_trainer.py:181] 1 batch: ips_loss=-2.7534916400909424, clamped_ips_loss=-2.7534916400909424, baseline_loss=0.0, max_ips=272.4482116699219, mean_ips=0.908729612827301, grad_update=True
I1003 063315.050 test_multi_gpu.py:156] rank=1 after train seq2slate param=tensor([-0.2485, 0.3616, -0.0977, -0.2214, 0.1736, 0.1298, -0.3060, -0.1304,\n ...], device='cuda:1', grad_fn=<CatBackward>)
I1003 063315.050 test_multi_gpu.py:161] rank=1 finish reading 1024 data
References
[1] https://www.telesens.co/2019/04/04/distributed-data-parallel-training-using-pytorch-on-aws/
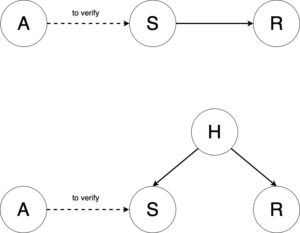
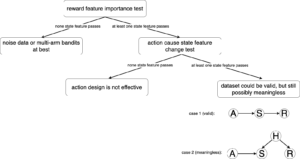

 This means at any time of A2C all workers and the global network always have the same parameters. Of course, the drawback of A2C is that the speed of one global gradient update is determined by the slowest worker.
This means at any time of A2C all workers and the global network always have the same parameters. Of course, the drawback of A2C is that the speed of one global gradient update is determined by the slowest worker. 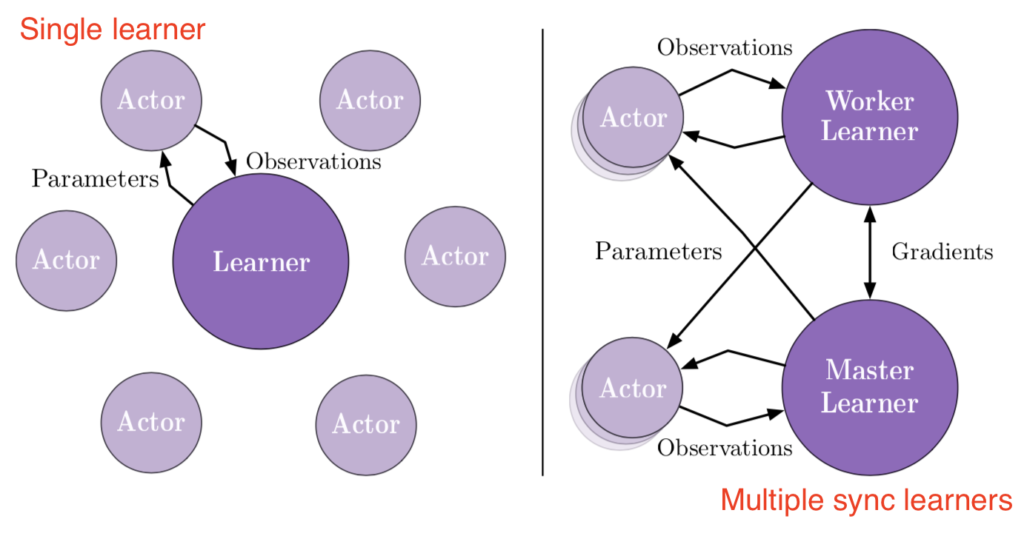
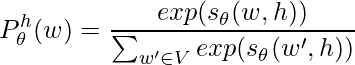
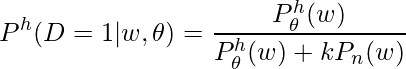
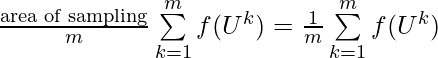
![Rendered by QuickLaTeX.com \frac{1}{m}\sum\limits_{k=1}^{m} z(u_1, u_2)\newline=\frac{1}{m}\sum\limits_{k=1}^{m} \left[f(u_1, u_2) -h(u_1, u_2) + \theta\right]\newline=\frac{1}{m}\sum\limits_{k=1}^{m} \left[exp[(u_1^2 + u_2^2)/2] - 1 - (u_1^2 + u_2^2)/2 + 4/3 \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-cefe400b6090655af28e4c28735815f6_l3.png) .
.
![Rendered by QuickLaTeX.com \nabla_\theta log \pi_\theta(a_t | s_t) R_t - h(s_t, a_t) + \mathbb{E}_{s\sim \rho_\pi, a \sim \pi}\left[ h(s_t, a_t)\right] \newline=\nabla_\theta log \pi_\theta(a_t | s_t) R_t - h(s_t, a_t) + \mathbb{E}_{s \sim \rho_\pi}\left[ \nabla_a Q_w(s_t, a)|_{a=\mu_\theta(s_t)} \nabla_\theta \mu_\theta(s_t)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9629b8ff4fc66089624196ff0d65190c_l3.png)
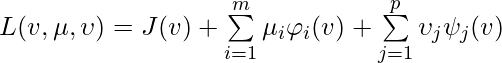 , where
, where 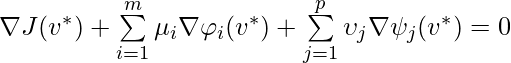
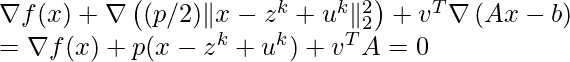
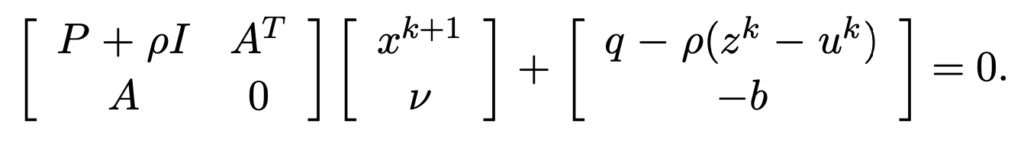




![Rendered by QuickLaTeX.com \[K(\mathbf{x}, \mathbf{y})=exp\left(-\frac{\|\mathbf{x}-\mathbf{y}\|^2}{2\sigma^2}\right),\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-b79b831a52476a21c48ca2567248e86f_l3.png)






![Rendered by QuickLaTeX.com \[f(t)=(g*h)(t)=\int^\infty_{-\infty}g(\tau)h(t-\tau)d\tau\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-237cc2257376e03764228a073433bafd_l3.png)
![Rendered by QuickLaTeX.com \[\hat{f}(\xi)=\int^{\infty}_{-\infty}f(t)e^{-2\pi i t \xi} dt\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-bdcf4fbf82c13fb6b7e8c2a58a4ae12d_l3.png)
![Rendered by QuickLaTeX.com \[f(t)=\int^\infty_{-\infty}\hat{f}(\xi)e^{2\pi i t \xi} d\xi\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-1c2eeeb000305a965a637e37ca7f52a0_l3.png)
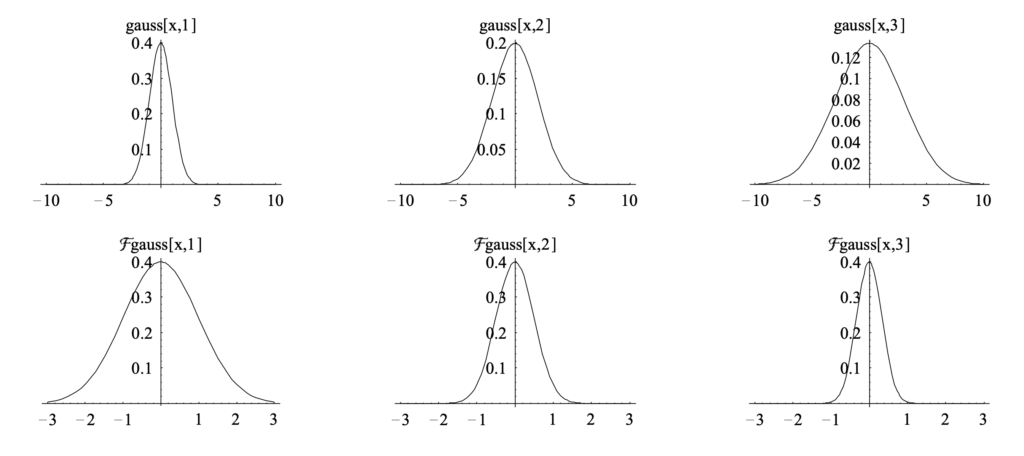
![Rendered by QuickLaTeX.com (g*h)(t)=\int^\infty_{-\infty}g(\tau)h(t-\tau)d\tau \newline=\int^\infty_{-\infty} g(\tau)\left[\int^\infty_{-\infty} \hat{h}(\xi) 2^{\pi i (t-\tau) \xi}d\xi\right]d\tau \newline=\int^\infty_{-\infty} \hat{h}(\xi) \left[\int^\infty_{-\infty} g(\tau) 2^{\pi i (t-\tau) \xi}d\xi\right]d\tau \quad \quad \text{swap } g(\tau)\text{ and }\hat{h}(\xi)\newline=\int^\infty_{-\infty} \hat{h}(\xi) \left[\int^\infty_{-\infty} g(\tau) 2^{-\pi i \tau \xi} d\tau\right] 2^{\pi i t \xi} d\xi\newline=\int^\infty_{-\infty} \hat{h}(\xi) \hat{g}(\xi) 2^{\pi i t \xi} d\xi \newline = IFT\left[\hat{h}(\xi) \hat{g}(\xi)\right] \quad\quad Q.E.D.](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-1771258be13b140b77c42f636647fb99_l3.png)


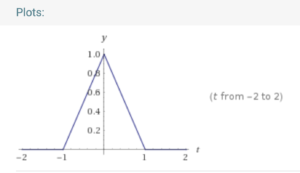
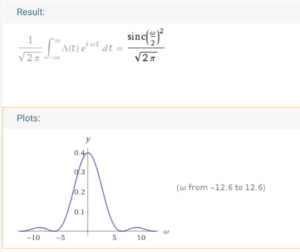
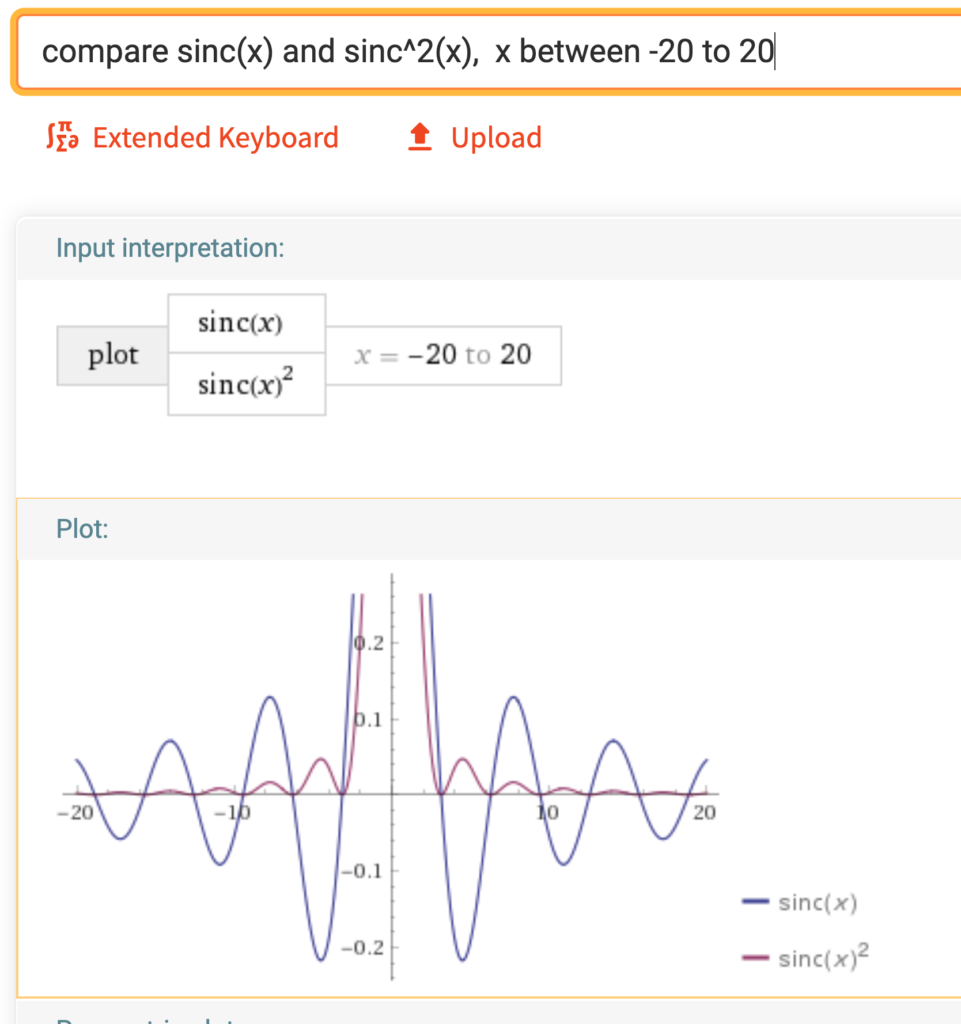
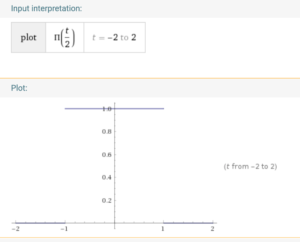 We know that its fourier transform is (
We know that its fourier transform is (
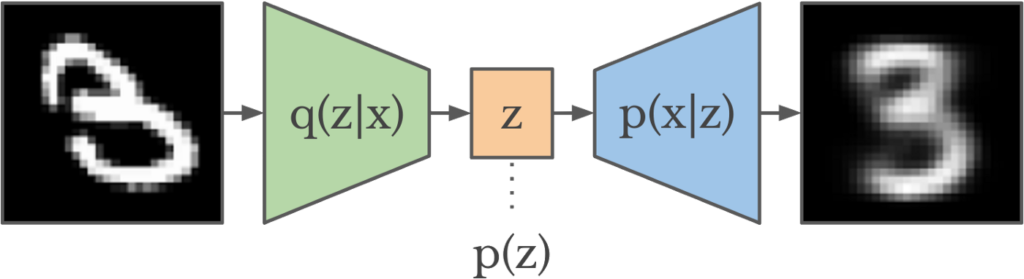
![Rendered by QuickLaTeX.com \theta^* = argmin_\theta\; KL\left(q_\theta(z|x) || p(z|x) \right ) \newline= argmin_\theta \; \mathbb{E}_{q_\theta} [log\;q_\theta(z|x)] - \mathbb{E}_{q_\theta} [log\;p(z,x)]+log\;p(x)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-1acb87f9932eec25d3692cac471a68aa_l3.png)
![Rendered by QuickLaTeX.com ELBO(\theta) \newline= \mathbb{E}_{q_\theta} [log\;p(z,x)] - \mathbb{E}_{q_\theta} [log\;q_\theta(z|x)]\newline=\mathbb{E}_{q_\theta}[log\;p(x|z)] + \mathbb{E}_{q_\theta}[log\;p(z)] - \mathbb{E}_{q_\theta}[log\;q_\theta(z|x)] \quad\quad p(z) \text{ is the prior of } z \newline= \mathbb{E}_{q_\theta}[log\;p(x|z)] - \mathbb{E}_{q_\theta} [log \frac{q_{\theta}(z|x)}{p(z)}]\newline=\mathbb{E}_{q_\theta}[log\;p(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-8e4bcee52335d51120c9eb549e33fe95_l3.png)
![Rendered by QuickLaTeX.com \begin{align*}&\nabla_\theta \left\{\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)\right\}\\=&\nabla_\theta \left\{\mathbb{E}_{q_\theta}\left[log\;p_\phi(x, z) - \log q_\theta(z|x)\right] \right\} \quad\quad \text{ rewrite KL divergence} \\ =&\nabla_\theta \; \int q_\theta(z|x) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]dz \\=& \int \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]\nabla_\theta q_\theta(z|x) dz + \int q_\theta(z|x) \nabla_\theta \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] dz \\=& \mathbb{E}_{q_\theta}\left[ \left(log\;p_\phi(x, z) - \log q_\theta(z|x) \right) \nabla_\theta \log q_\theta(z|x) \right] + \mathbb{E}_{q_\theta}\left[\nabla_\theta \log p_\phi(x, z)\right] + \mathbb{E}_{q_\theta}\left[ \nabla_\theta \log q_\theta(z|x) \right] \\&\text{--- The second term is zero because no }\theta \text{ in } \log p_\phi(x,z) \\&\text{--- The third term being zero is a common trick. See Eqn. 5 in [1]} \\=& \mathbb{E}_{q_\theta}\left[ \left(log\;p_\phi(x, z) - \log q_\theta(z|x) \right) \nabla_\theta \log q_\theta(z|x) \right]\end{align*}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-ab36fc8bea2fc218505d19ee6e54e94c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*}&\nabla_\theta \left\{\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)\right\}\\=&\nabla_\theta \left\{\mathbb{E}_{q_\theta}\left[log\;p_\phi(x, z) - \log q_\theta(z|x)\right] \right\} \quad\quad \text{ rewrite KL divergence} \\=&\nabla_\theta \; \int q_\theta(z|x) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]dz \\=&\nabla_\theta \; \int p(\epsilon) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]d\epsilon \quad\quad \\&\text{--- Above uses the property of changing variables in probability density functions.} \\&\text{--- See discussion in [10, 11]} \\=& \int p(\epsilon) \nabla_\theta \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]d\epsilon \\=& \int p(\epsilon) \nabla_z \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] \nabla_\theta z d\epsilon \\=& \mathbb{E}_{p(\epsilon)} \left[ \nabla_z \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] \nabla_\theta f_\theta(x) \right]\end{align*}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-4fafc4bcaae654c035173052feaa8981_l3.png)

![Rendered by QuickLaTeX.com \mathbb{E}_{p(x)}[f(x)]\approx \frac{1}{N}\sum\limits_{i=1}^Nf(x_i)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-6cea83b1e26813296576c469c343b9b0_l3.png)
![Rendered by QuickLaTeX.com \mathbb{E}_{p(x)}[z(x)]\newline=\mathbb{E}_{p(x)}[f(x)]-\mathbb{E}_{p(x)}[h(x)] + \theta\newline=\mathbb{E}_{p(x)}[f(x)]-\theta + \theta\newline=\mathbb{E}_{p(x)}[f(x)]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-119a2e3969f356586cea4c664bcffc85_l3.png)
![Rendered by QuickLaTeX.com Var_{p(x)}[z(x)] \newline = Var_{p(x)}\left[f(x) - h(x)+\theta\right] \newline = Var_{p(x)}\left[f(x)-h(x)\right] \quad \quad \text{constant doesn't contribute to variance}\newline=\mathbb{E}_{p(x)}\left[\left(f(x)-h(x)-\mathbb{E}_{p(x)}\left[f(x)-h(x)\right] \right)^2\right] \quad\quad Var(x)=\mathbb{E}[(x-\mathbb{E}(x))^2] \newline=\mathbb{E}_{p(x)}\left[\left( f(x)-\mathbb{E}_{p(x)}[f(x)] - \left(h(x)-\mathbb{E}_{p(x)}[h(x)]\right) \right)^2\right]\newline=\mathbb{E}_{p(x)}\left[\left(f(x)-\mathbb{E}_{p(x)}[f(x)]\right)^2\right] + \mathbb{E}_{p(x)}\left[\left(h(x)-\mathbb{E}_{p(x)}[h(x)]\right)^2\right] \newline - 2 * \mathbb{E}_{p(x)}\left[f(x)-\mathbb{E}_{p(x)}[f(x)]\right] * \mathbb{E}_{p(x)}\left[h(x)-\mathbb{E}_{p(x)}[h(x)]\right]\newline=Var_{p(x)}\left[f(x)\right]+Var_{p(x)}\left[h(x)\right] - 2 * Cov_{p(x)}\left[f(x), h(x)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-0ccdbafc7e844065190f08449216de2b_l3.png)
![Rendered by QuickLaTeX.com Var_{p(x)}[z(x)] \newline=Var_{p(x)}\left[f(x)\right]+c^2 \cdot Var_{p(x)}\left[h(x)\right] + 2c * Cov_{p(x)}\left[f(x), h(x)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-17bc7bdff9ac5e1ae313fbe74320b19d_l3.png) ,
,![Rendered by QuickLaTeX.com Var^*_{p(x)}[z(x)] \newline=Var_{p(x)}\left[f(x)\right] - \frac{\left(Cov_{p(x)}\left[f(x), h(x)\right] \right)^2}{Var_{p(x)}[h(x)]}\newline=\left(1-\left(Corr_{p(x)}\left[f(x),h(x)\right]\right)^2\right)Var_{p(x)}\left[f(x)\right] \quad\quad Corr(x,y)=Cov(x,y)/stdev(x)stdev(y)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-397f1651dac767c2187126a6a9a18978_l3.png)
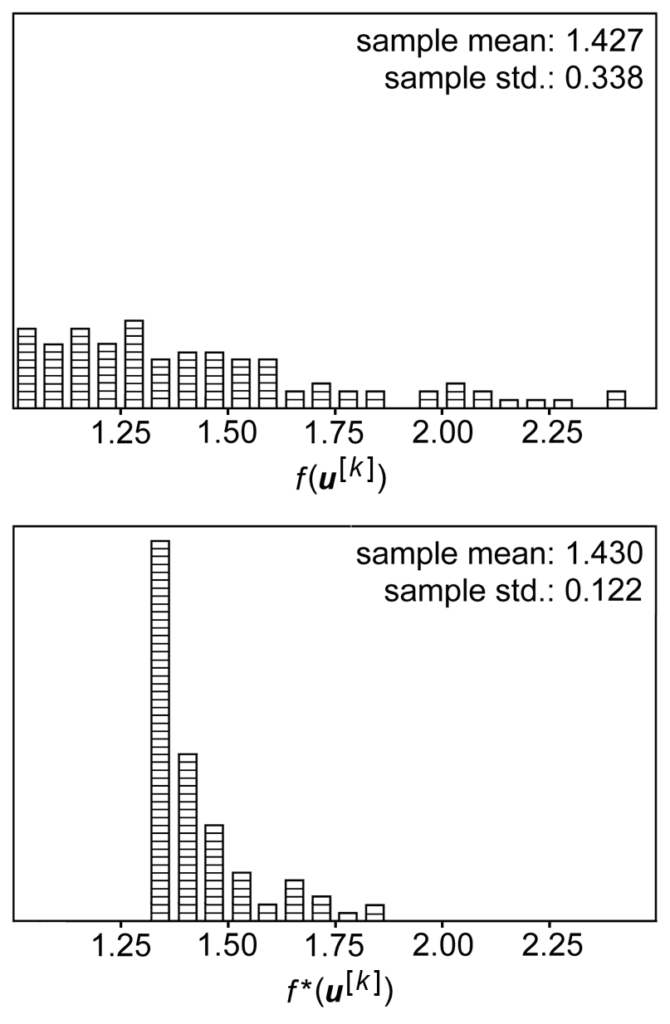
![Rendered by QuickLaTeX.com Var_{p(x)}[z(x)] \newline =Var_{p(x)}\left[f(x)\right]+Var_{p(x)}\left[h(x)\right] - 2 * Cov_{p(x)}\left[f(x), h(x)\right]\newline =\frac{8000}{9} + \frac{25}{3}-\frac{2\cdot 250}{3}\newline=\frac{6575}{9}<Var_{p(x)}[f(x)]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-386cf1266b42bd8a666f8421d6b2e6c5_l3.png) .
.![Rendered by QuickLaTeX.com Var_{p(x)}[\bar{z}(x)]=Var_{p(x)}\left[\frac{\sum\limits_{i=1}^N z(x_i)}{N}\right]=N \cdot Var_{p(x)}\left[\frac{z(x)}{N}\right]=\frac{Var_{p(x)}\left[z(x)\right]}{N}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-8689d39a37054b16c04ad196608819f2_l3.png) . This matches with our intuition that the more samples you average over, the less variance you have. However, the relative ratio of variance you can save by introducing
. This matches with our intuition that the more samples you average over, the less variance you have. However, the relative ratio of variance you can save by introducing