Learning a policy that can optimize multiple types of rewards or satisfy different constraints is a much desired feature in the industry. In real products, we often care about not only single one metric but several that interplay with each other. For example, we want to derive a policy to recommend news feeds which expects to increase impressions but should not regress the number of likes, follows, and comments.
The vein of multi-objective and constrained RL is an active research area. Before we proceed, I want to clarify the definition of multi-objective RL and constrained RL in my own words. Multi-objective RL focuses on optimizing multiple objectives in the same time. For one reward type, the question is how we can maximize this reward type without reducing any of other rewards. Therefore, multi-objective RL usually needs to fit the whole Pareto Frontier. Constrained RL is somewhat relaxed because its focused question is how we can maximize this reward type while other rewards are no worse than specified constraints (which don’t need to be “not reduce any of other rewards).
Multi-Objective RL
Constrained RL
[1] introduces an algorithm called ApproPO to answer the feasibility problem and return the best policy if the problem is feasible. The feasibility problem is defined as:
![]()
which can be expressed as a distance objective:
![]()
Here, ![]() denotes all possible mixed policies so you should think
denotes all possible mixed policies so you should think ![]() as a probability distribution over finitely many stationary policies.
as a probability distribution over finitely many stationary policies. ![]() is a
is a ![]() -dimensional return measurement vector (i.e.,
-dimensional return measurement vector (i.e., ![]() is the number of rewards over which we specify constraints).
is the number of rewards over which we specify constraints). ![]() could then be thought as a weighted sum of returns of individual stationary policies:
could then be thought as a weighted sum of returns of individual stationary policies: ![]() .
. ![]() is the convex set of constraints. Why couldn’t we just get one single stationary policy as the answer? It seems to me that ApproPO has to return a mixture of policies because the author chooses to solve the minimization problem by solving a two-player game based on game theory, which suggests “the average of their plays converges to the solution of the game”.
is the convex set of constraints. Why couldn’t we just get one single stationary policy as the answer? It seems to me that ApproPO has to return a mixture of policies because the author chooses to solve the minimization problem by solving a two-player game based on game theory, which suggests “the average of their plays converges to the solution of the game”.
Here is the stretch of how the authors solve the minimization problem by solving a two-player game.
- For a convex cone
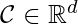 and any point
and any point 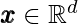 , we define the dual convex cone
, we define the dual convex cone 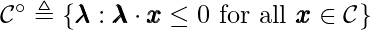 .
. - According to Lemma 3.2,
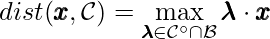 . Plugging this Lemma into the minimization problem we actually care about, we obtain a min-max game (with
. Plugging this Lemma into the minimization problem we actually care about, we obtain a min-max game (with 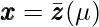 ):
): 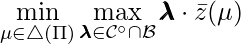 .
. - The min-max formula satisfies certain conditions (as shown in the paragraph above Eqn. (9) in the paper [1]) such that it is equivalent to a max-min game:
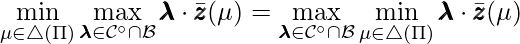 .
. - In the max-min game, the
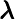 -player plays first, and the
-player plays first, and the 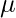 -player plays next. And their turns can continue incessantly. Theory has shown that if the
-player plays next. And their turns can continue incessantly. Theory has shown that if the 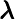 -player keeps using a no-regret algorithm repeatedly against
-player keeps using a no-regret algorithm repeatedly against 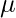 -player who uses a best response algorithm, then “the averages of their plays converge to the solution of the game”.
-player who uses a best response algorithm, then “the averages of their plays converge to the solution of the game”. - There is an off-the-shelf no-regret algorithm called online gradient descent (OGD) which can be used by
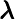 -player. We won’t cover the details of this algorithm in this post. Given any
-player. We won’t cover the details of this algorithm in this post. Given any 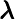 returned by
returned by 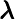 palyer, the best response algorithm used by
palyer, the best response algorithm used by 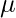 -player will need to find
-player will need to find 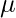 such that
such that 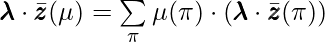 is minimized. The implicit conditions that the best response algorithm’s solution should also satisfy are
is minimized. The implicit conditions that the best response algorithm’s solution should also satisfy are 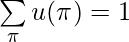 and
and 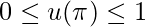 for
for 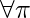 .
. - Based on properties of linear programming, we know the best response algorithm’s solution must be on a corner point. This can be translated into finding a single stationary policy
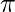 which optimizes the return with the scalar reward
which optimizes the return with the scalar reward 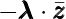 . Such a
. Such a 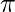 will be found using any preferred RL algorithm on the MDP.
will be found using any preferred RL algorithm on the MDP. - After
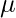 -player returns the best
-player returns the best 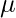 ,
, 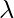 -player can again return a new
-player can again return a new 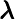 based on
based on 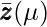 . Then
. Then 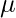 -player again returns the best policy learned on the scalar reward
-player again returns the best policy learned on the scalar reward 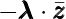 . The iterations go on for
. The iterations go on for 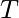 steps. Finally the algorithm would return a random mixture of
steps. Finally the algorithm would return a random mixture of 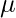 from all iteration steps.
from all iteration steps.

My concern is that this algorithm could not easily be extended to the batch learning context. Although the best response algorithm can always use an off-policy algorithm to learn ![]() without recollecting data, determining the optimal
without recollecting data, determining the optimal ![]() needs to know
needs to know ![]() , the estimation of
, the estimation of ![]() on all dimensions of rewards. This would be super inaccurate using any off-policy evaluation method. There is also a question on how to serve the mixture of policies rather than just one single policy.
on all dimensions of rewards. This would be super inaccurate using any off-policy evaluation method. There is also a question on how to serve the mixture of policies rather than just one single policy.
References
[1] Reinforcement Learning with Convex Constraints