Policy Gradient

Reinforcement learning algorithms can be divided into many families. In model-free temporal difference methods like Q-learning/SARSA, we try to learn action value $latex Q(s,a)$ for any state-action pair, either by recording (“memorizing”) exact values in a tabular or learning a function to approximate it. Under $latex \epsilon$-greedy, the action to be selected at a state will therefore be $latex argmax_a Q(s,a)$ but there is also a small constant chance $latex \epsilon$ to be any non-optimal action.

Another family is called policy gradient methods which directly map states to actions. To select actions, they do not need to consult a value table or a value function. Instead, each action can be selected with a probability determined by a parameterized policy function $latex \pi(a|s,\theta)$, where $latex \theta$ is the policy function’s parameters.

The advantages of policy gradient methods over Q-learning/SARSA using $latex \epsilon$ greedy are mainly two:

1. in some situations the optimal approximate policy must be stochastic.  An example from [1]: in card games with imperfect information the optimal play is often to do two different things with specific probabilities, such as when bluffing in Poker. Action-value methods have no natural way of finding stochastic optimal policies.
2. problems vary in the complexity of their policies and action-value functions. In some problems, the policy is a much simpler function to approximate than action-values so it will be faster to learn

The general update form of policy gradient methods is $latex \theta_{t+1} = \theta_t + \alpha \nabla \eta(\theta_t)$, where $latex \eta(\theta_t)$ is performance measure with respect to the policy weights.

Now, the policy gradient theorem can be briefly described as [5]:

In episodic case, the policy gradient theorem derives as follows (according to [1]):

The last expression is an exact formula of the gradient of $latex \eta(\theta)$. It can also be seen as an expectation of $latex \gamma^t \sum\limits_{a_t} \nabla_\theta \pi(a_t|s_t) q(s_t, a_t)$ over the probability distribution of landing on $latex s_t$ in $latex t$ steps. Please note for any fixed $latex t$, $latex \sum\limits_{s_t} \Pr(s_0 \rightarrow s_t, t, \pi)=1$. Therefore, we can rewrite the above last expression as an expectation form:

where $latex \qquad G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} + \cdots$. $latex G_t$ is an unbiased estimator of $latex q(s_t, a_t)$ in the last two steps since we do not have estimation for $latex q(s_t, a_t)$. We use $latex \mathbb{E}_{\pi}$ to replace $latex \mathbb{E}_{s_t \sim \Pr(s_0 \rightarrow s_t, t, \pi) \atop a_t \sim \pi(a_t | s_t)} &s=2$, meaning that the sequence $latex S_0, A_0, S_1, A_1, \cdots$ are generated following the policy $latex \pi(a_t|s_t)$ and the transition probability $latex p(s_{t+1}|s_t, a_t)$. Sometimes we can also write $latex \mathbb{E}_{\pi_\theta}$ because the policy $latex \pi$ is parameterized by $latex \theta$. We can also write $latex \mathbb{E}_{\pi}$ as $latex \mathbb{E}_{s_{0:T}, a_{0:T}}$. In other words, $latex \nabla \eta(\theta) = \mathbb{E}_{s_{0:T}, a_{0:T}}[\sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t|s_t)] &s=2$

What we do in reality is to use these collected state, actions and rewards as samples to approximate the exact expectation of $latex \nabla \eta(\theta)$:

This kind of policy gradient method is called REINFORCE, by Ronald J. Williams from Northeastern University. The original paper [2] is hard to read in my opinion. It directly tells you what is the update rule of $latex \theta$ by construction, and then tells you the expected update aligns in the same direction as the performance gradient. What I wish to be told is how he derived the update rule of $latex \theta$ in the first place.

(Updated 09/18/2017: The same derivative procedure of REINFORCE is illustrated more clearly in [10])

(Updated 01/31/2020: The derivative procedure of REINFORCE in continuous state/action space is illustrated in [15])

One important extension of REINFORCE is to offsetting $latex G_t$ by a baseline $latex b(s_t)$, a function of $latex s_t$. Intuitively, we need not how good an action is, but how much better this action is compared to average actions. For example, if $latex G_t$ is uniformly larger than zero for either good or bad actions, $latex \theta$ will always get updated to encourage either kind of actions. We need to calibrate $latex G_t$ such that it can differentiate good or bad actions better. Mathematically, adding a baseline can reduce the variance of $latex \nabla \eta(\theta)$ while still keeping it as unbiased estimator.

First, let’s look at why offsetting $latex G_t$ by $latex b(s_t)$ still makes $latex \nabla \eta(\theta)$ an unbiased estimator (reference from [8]):

To ensure $latex \mathbb{E}_{s_{0:T}, a_{0:T}} [\sum\limits_{t=0}^T \gamma^t (G_t – b(s_t)) \nabla_\theta \log \pi (a_t|s_t)]$ is an unbiased estimate of $latex \nabla \eta(\theta)$, $latex b(s_t)$ should only be a function of $latex s_t$, but not $latex a_t$. Otherwise $latex \mathbb{E}_{s_{0:T}, a_{0:T}}[\sum\limits_{t=0}^T \gamma^t b(s_t) \nabla_\theta \log \pi (a_t | s_t)]$ is not zero.

It is less obvious that adding $latex b(s_t)$ can reduce the variance of $latex Var[ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)]$ .

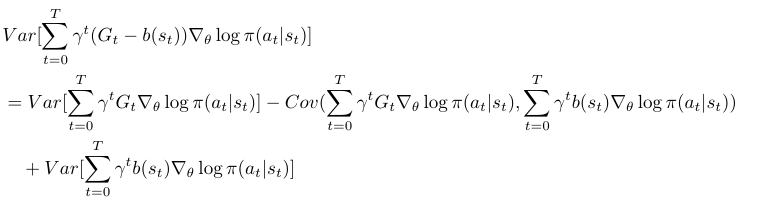
From here, we can see if $latex \sum\limits_{t=0}^T \gamma^t b(s_t) \nabla_\theta \log \pi(a_t | s_t)$ has large enough covariance with $latex \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)$ to outweigh its own variance, then the variance is reduced. Unrealistically, if $latex b(s_t) = G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} + \cdots$, then variance will be zero, although this is impossible because $latex b(s_t)$ is only a function of $latex s_t$ without magic forecast ability to 100% approach $latex G_t$.

(sidenote: I cannot follow [8]’s deduction on variance reduction part.)

One way is to train a predictor on $latex \hat{v}(S_t | w)$ with parameter $latex w$ as a baseline:

REINFORCE is an on-policy algorithm because $latex \delta=G_t – \hat{v}(S_t,w)$ in the gradient update depends on $latex G_t$, the returns generated by following the current policy $latex \pi_\theta$. The specific one-step actor-critic algorithm we just described is also an on-policy algorithm because $latex \delta=R+\gamma \hat{v}(S’, w) – \hat{v}(S, w)$ depends on the next state $latex S’$ which is the result of applying $latex \pi_\theta$ at the current state $latex S$.  There also exists off-policy actor-critics, see an overview of on-policy and off-policy policy gradient methods at [14].

A more recent advance in baseline is Generalized Advantage Estimation (GAE) [6]. They introduce two parameters, $latex \gamma$ and $latex \lambda$, in an un-discounted reward problem to help estimate $latex g:=\nabla_\theta \mathbb{E}[\sum_{t=0}^\infty] r_t$ with little introduced bias and reduced variance. (Note that how discounted reward problems can be transformed into an un-discounted problem: “But the discounted problem (maximizing $latex \sum_{t=0}^\infty \gamma^t r_t)$ can be handled as an instance of the undiscounted problem in which we absorb the discount factor into the reward function, making it time-dependent.”)

They introduce their notations:

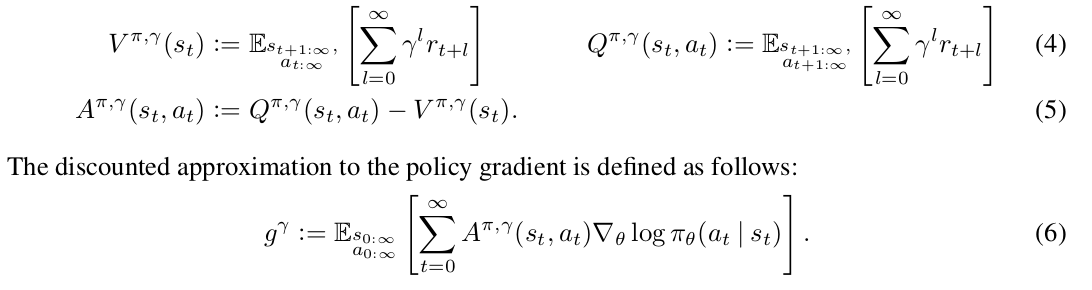
Note that $latex g^\gamma$ is a biased estimator of $latex g$ but as they claim previous works have studied to “reduce variance by downweighting rewards corresponding to delayed effects, at the cost of introducing bias”.

The paper’s goal is to find a good estimator of $latex A^{\pi, \gamma}$ which is called $latex \hat{A}_t$.

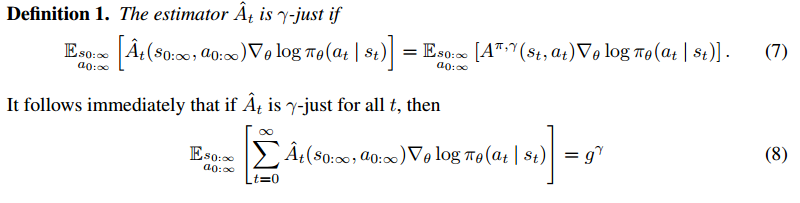
In other word, if $latex \hat{A}_t$ is $latex \gamma$-just, then it helps to construct an unbiased estimator of $latex g^\gamma$. Equation (8) just uses the property that the expectation of a sum equals to the sum of expectations.

Now, what other property does $latex \hat{A}_t$ have? If we know any property of $latex \hat{A}_t$, it will help us find $latex \hat{A}_t$ more easily. The paper proposes one property:

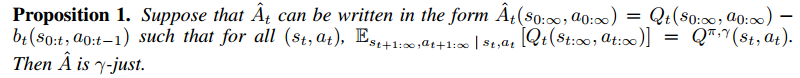
Sketch proof of proposition 1:

First of all, to understand the notations clearly, think that $latex \hat{A}_t(s_{0:\infty}, a_{0:\infty})$ and $latex Q_t(s_{0:\infty}, a_{0:\infty})$ are functions with input as the whole trajectory $latex s_0, a_0, s_1, a_1, \cdots$. Similarly, think $latex b_t(s_{0:t}, a_{0:t-1})$ as a function with the input as the former part of the trajectory $latex s_0, a_0, s_1, a_1, \cdots, s_t$.

Now, suppose a satisfied $latex \hat{A}_t$ such that $latex \hat{A}_t(s_{0:\infty}, a_{0:\infty}) = Q_t(s_{0:\infty}, a_{0:\infty}) – b_t(s_{0:t}, a_{0:t-1})$ where for all $latex (s_t, a_t), \; \mathbb{E}_{s_{t+1:\infty}, a_{t+1:\infty}|s_t,a_t} = Q^{\pi,\gamma}(s_t, a_t)$, then:

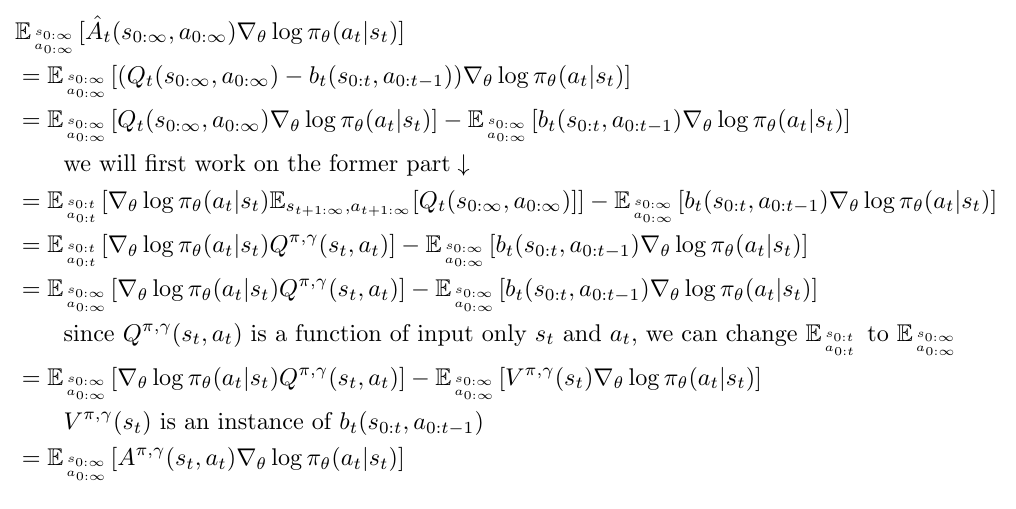
Next, they find a good candidate function for $latex \hat{A}_t$, which is $latex \delta_t^V = r_t + \gamma V(s_{t+1}) – V(s_t)$. Only when we know $latex V = V^{\pi, \gamma}$ is $latex \delta_t^V$ $latex \gamma$-just. Otherwise $latex V$ is a biased estimator of $latex g^\gamma$. However, if we can take average of different variations of $latex \delta$ (equation 11, 12, 13, 14, 15, and 16), then we might get a low bias, low variance estimator, which is called $latex GAE(\gamma, \lambda)$.

$latex \hat{A}_t:=GAE(\gamma, 1)$ is $latex \gamma$-just regardless of the accuracy of $latex V$ (again, this is because $latex E_{s_{0:\infty}, a_{0:\infty}}[V(s_t) \nabla_\theta \log \pi_\theta (a_t | s_t) ] = 0$). However $latex GAE(\gamma, 1)$ is believed (I don’t know how to prove that) to have high variance due to the long sum of rewards. On the other extreme end, $latex GAE(\gamma, 0)$ has low variance but since we are estimating the value function $latex V$, $latex GAE(\gamma, 0)$  must be a biased estimator of $latex g^\gamma$. $latex GAE(\gamma, \lambda)$ with $latex 0<\lambda<1$ would make a trade-off between variance and bias.

Update 2018-11-08

Policy gradient is better illustrated in several recent posts: [11] and [12]

Reference

[1] Reinforcement learning: An introduction

[2] Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning

[3] https://medium.com/emergent-future/simple-reinforcement-learning-with-tensorflow-part-8-asynchronous-actor-critic-agents-a3c-c88f72a5e9f2

[4] Asynchronous Methods for Deep Reinforcement Learning

[5] http://www.breloff.com/DeepRL-OnlineGAE/

[6] HIGH-DIMENSIONAL CONTINUOUS CONTROL USING GENERALIZED ADVANTAGE ESTIMATION

[7] Variance Reduction Techniques for Gradient Estimates in Reinforcement Learning

[8] https://danieltakeshi.github.io/2017/03/28/going-deeper-into-reinforcement-learning-fundamentals-of-policy-gradients/

[9] https://danieltakeshi.github.io/2017/04/02/notes-on-the-generalized-advantage-estimation-paper/

[10] https://www.youtube.com/watch?v=kUiR0RLmGCo

[11] https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html#soft-actor-critic

[12] https://spinningup.openai.com/en/latest/spinningup/rl_intro3.html#expected-grad-log-prob-lemma

[13] Supplement material of DeepMimic: Example-Guided Deep Reinforcement Learning of Physics-Based Character Skills

[14] Unifying On-Policy and Off-Policy Learning

[15] http://web.stanford.edu/class/cme241/lecture_slides/PolicyGradient.pdf

latex for policy gradient theorem:

\begin{align*}
\nabla \eta(\theta) &= \nabla_\theta v_{\pi} (s_0) \quad \quad \text{performance measure is the value of starting state} \\
&= \nabla_\theta \big[ \sum\limits_{a_0} \pi(a_0|s_0) q(s_0,a_0) \big] \\
&=\sum\limits_{a_0} \big[ \nabla_\theta \pi(a_0|s_0) q(s_0, a_0) + \pi(a_0|s_0) \nabla_\theta q(s_0, a_0) \big]  \quad \quad \text{derivative product rule} \\ 
&= \sum\limits_{a_0} \Big[ \nabla_\theta \pi(a_0|s_0) q(s_0, a_0) + \pi(a_0|s_0) \nabla_\theta \big[ \sum\limits_{s_1,r_0} p(s_1, r_0 |s_0,a_0)(r_0 + \gamma v_\pi(s_1)) \big] \Big] \\
&= \sum\limits_{a_0} \big[ \nabla_\theta \pi (a_0 | s_0) q(s_0, a_0) + \pi(a_0 | s_0) \sum\limits_{s_1} \gamma p(s_1| s_0, a_0) \nabla_\theta v_{\pi}(s_1) \big] \qquad r \text{ has nothing to do with regard to } \theta \\ 
& \qquad \text{up till now, we have a recursion:} \\
& \qquad \nabla_\theta v_\pi(s_t)= \sum\limits_{a_t} \Big[ \nabla_\theta \pi(a_t|s_t) q(s_t, a_t) + \pi(a_t|s_t) \big[ \sum\limits_{s_{t+1}} \gamma p(s_{t+1}|s_t,a_t) \nabla_\theta v_\pi(s_{t+1}) \big] \Big]  \\
&=\sum\limits_{a_0} \Big[ \nabla_\theta \pi (a_0 | s_0) q(s_0, a_0) + \pi(a_0 | s_0) \sum\limits_{s_1} \gamma p(s_1| s_0, a_0) \\ & \qquad \qquad  \sum\limits_{a_1} \big[ \nabla_\theta \pi(a_1 | s_1)q(s_1, a_1) + \pi(a_1 | s_1)\sum\limits_{s_2} \gamma p(s_2|s_1, a_1) \nabla_\theta v_{\pi} (s_2) \big] \Big]  \\
&=\sum\limits_{a_0} \nabla_\theta \pi (a_0 | s_0) q(s_0, a_0) \\
& \qquad +  \gamma \sum\limits_{s_1} \sum\limits_{a_0} p(s_1| s_0, a_0) \pi(a_0 | s_0)  \sum\limits_{a_1}  \nabla_\theta \pi(a_1 | s_1)q(s_1, a_1) \\
& \qquad + \gamma^2 \sum\limits_{s_2} \sum\limits_{a_1} \sum\limits_{s_1} \sum\limits_{a_0} p(s_2|s_1, a_1) \pi(a_1 | s_1) p(s_1| s_0, a_0) \pi(a_0 | s_0) \nabla_\theta v_{\pi} (s_2)  \\
&= \cdots \qquad \text{(keep unrolling using the recursion)}\\
&= \sum\limits_{t=0}^\infty \sum\limits_{s_t} \gamma^t \Pr(s_0 \rightarrow s_t, t, \pi) \sum\limits_{a_t} \nabla_\theta \pi(a_t | s_t) q(s_t, a_t)  \qquad  \Pr(s_0 \rightarrow s_t, t, \pi) \text{ is the prob. of } s_0 \text{ to } s_t \text{ in } t \text{ steps} 
\end{align*}

latex for expectation form rewritten:

\begin{align*}
\nabla \eta(\theta) &= \sum\limits_{t=0}^\infty \sum\limits_{s_t} \gamma^t \Pr(s_0 \rightarrow s_t, t, \pi) \sum\limits_{a_t} \nabla_\theta \pi(a_t | s_t) q(s_t, a_t) \\
&=\sum\limits_{t=0}^\infty \mathbb{E}_{s_t \sim \Pr(s_0 \rightarrow s_t, t, \pi)}[\sum\limits_{a_t} \gamma^t \nabla_\theta \pi(a_t | s_t) q(s_t, a_t) ] \\ 
&=\sum\limits_{t=0}^\infty \mathbb{E}_{s_t \sim \Pr(s_0 \rightarrow s_t, t, \pi)} [\sum\limits_{a_t} \gamma^t \pi(a_t | s_t) q(s_t, a_t) \frac{\nabla_\theta \pi(a_t | s_t)}{\pi(a_t | s_t)} ] \\
&=\sum\limits_{t=0}^\infty \mathbb{E}_{s_t \sim \Pr(s_0 \rightarrow s_t, t, \pi) \atop a_t \sim \pi(a_t | s_t) \quad}[ \gamma^t q(s_t, a_t) \frac{\nabla_\theta \pi(a_t | s_t)}{\pi(a_t | s_t)}] \\
&=\sum\limits_{t=0}^\infty \mathbb{E}_{s_t \sim \Pr(s_0 \rightarrow s_t, t, \pi) \atop a_t \sim \pi(a_t | s_t) \quad}[ \gamma^t q(s_t, a_t) \nabla_\theta \log \pi(a_t | s_t)]  \qquad \nabla \log(x) = \frac{\nabla x}{x} \\ 
&=\mathbb{E}_{\pi}[ \sum\limits_{t=0}^\infty \gamma^t q(s_t, a_t) \nabla_\theta \log \pi(a_t | s_t)] \\ 
&=\mathbb{E}_{\pi}[ \sum\limits_{t=0}^\infty \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)]
\end{align*}

latex for adding baseline is still unbiased estimator:

\begin{align*}
&\mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t (G_t - b(s_t)) \nabla_\theta \log \pi(a_t | s_t)] \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \mathbb{E}_{s_{0:T}, a_{0:T}}[ \sum\limits_{t=0}^T \gamma^t  b(s_t) \nabla_\theta \log \pi (a_t | s_t) ] \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \mathbb{E}_{s_{0:T}, a_{0:T}}[ \gamma^t  b(s_t) \nabla_\theta \log \pi (a_t | s_t) ]  \qquad \text{exp. of sum equals to sum of exp.}\\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \mathbb{E}_{s_{t}, a_{t}}[ \gamma^t  b(s_t) \nabla_\theta \log \pi (a_t | s_t) ] \qquad \text{remove irrelevant variables in each exp.}\\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \sum\limits_{s_{t}} \sum\limits_{a_{t}} p(s_t, a_t)  \gamma^t  b(s_t) \nabla_\theta \log \pi (a_t | s_t)  \qquad \text{expectation form} \rightarrow \text{discrete sum} \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \sum\limits_{s_{t}} \sum\limits_{a_{t}} p(s_t) \pi(a_t|s_t)  \gamma^t  b(s_t) \frac{\nabla_\theta \pi (a_t | s_t)}{\pi(a_t | s_t) }  \qquad \text{rule of probability} \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \sum\limits_{s_{t}} \gamma^t  b(s_t) p(s_t) \sum\limits_{a_{t}} \nabla_\theta \pi (a_t | s_t)  \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \sum\limits_{s_{t}} \gamma^t  b(s_t) p(s_t) \nabla_\theta \sum\limits_{a_{t}} \pi (a_t | s_t)  \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] - \sum\limits_{t=0}^T \sum\limits_{s_{t}} \gamma^t  b(s_t) p(s_t) \nabla_\theta 1  \\
=& \mathbb{E}_{s_{0:T}, a_{0:T}} [ \sum\limits_{t=0}^T \gamma^t G_t \nabla_\theta \log \pi(a_t | s_t)] \\
=& \nabla \eta(\theta) 
\end{align*}

latex for sketch proof of proposition 1:

\begin{align*}
&\mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}} [\hat{A}_t(s_{0:\infty}, a_{0:\infty}) \nabla_\theta \log \pi_\theta(a_t | s_t) ] \\
&= \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}} [(Q_t(s_{0:\infty}, a_{0:\infty}) - b_t(s_{0:t}, a_{0:t-1})) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&= \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[Q_t(s_{0:\infty}, a_{0:\infty}) \nabla_\theta \log \pi_\theta(a_t | s_t)] - \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[b_t(s_{0:t}, a_{0:t-1}) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&\qquad \text{we will first work on the former part} \downarrow \\
&= \mathbb{E}_{s_{0:t} \atop a_{0:t}}[\nabla_\theta \log \pi_\theta(a_t | s_t) \mathbb{E}_{s_{t+1:\infty}, a_{t+1:\infty}} [Q_t(s_{0:\infty}, a_{0:\infty})] ] - \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[b_t(s_{0:t}, a_{0:t-1}) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&= \mathbb{E}_{s_{0:t} \atop a_{0:t}}[\nabla_\theta \log \pi_\theta(a_t | s_t) Q^{\pi, \gamma}(s_t, a_t)] - \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[b_t(s_{0:t}, a_{0:t-1}) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&= \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[\nabla_\theta \log \pi_\theta(a_t | s_t) Q^{\pi, \gamma}(s_t, a_t)] - \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[b_t(s_{0:t}, a_{0:t-1}) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&\qquad \text{since } Q^{\pi, \gamma}(s_t, a_t) \text{ is a function of input only } s_t \text{ and } a_t \text{, we can change } \mathbb{E}_{s_{0:t} \atop a_{0:t}} \text{ to } \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}} \\
&= \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[\nabla_\theta \log \pi_\theta(a_t | s_t) Q^{\pi, \gamma}(s_t, a_t)] - \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}}[V^{\pi, \gamma}(s_t) \nabla_\theta \log \pi_\theta(a_t | s_t)] \\
&\qquad V^{\pi, \gamma}(s_t) \text{ is an instance of } b_t(s_{0:t}, a_{0:t-1})  \\
&= \mathbb{E}_{s_{0:\infty} \atop a_{0:\infty}} [A^{\pi, \gamma}(s_t, a_t) \nabla_\theta \log \pi_\theta(a_t | s_t) ]
\end{align*}