In a previous post, we discussed an earlier generative modeling called Normalizing Flows [1]. However, Normalizing Flows has its own limitations: (1) it requires the flow mapping function ![]() to be invertible. This limits choices of potential neural network architectures to instantiate
to be invertible. This limits choices of potential neural network architectures to instantiate ![]() , because being invertible means that hidden layers must have the exact same dimensionality as the input. (2) computing the log of determinant of the jacobian matrix of
, because being invertible means that hidden layers must have the exact same dimensionality as the input. (2) computing the log of determinant of the jacobian matrix of ![]() is expensive, usually in
is expensive, usually in ![]() time complexity.
time complexity.
Flow matching is a more recent developed generative modeling technique with lower training cost (see the comparison between Normalizing Flows vs Flow Matching in [2] and a more mathematical introduction of how Flow Matching evolved from Normalizing Flows [6]). In this post, we are going to introduce it. Two materials help me understand flow matching greatly: (1) neurips flow matching tutorial [3] (2) an MIT teaching material [4]

Flow Matching
Motivation
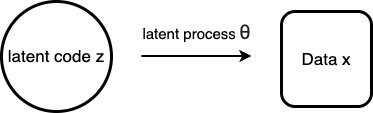
We start from the motivation. Suppose ![]() represents the target space we want to generate (e.g., all dog pictures with
represents the target space we want to generate (e.g., all dog pictures with ![]() representing the image dimension). The goal of generative modeling is to learn the real target distribution
representing the image dimension). The goal of generative modeling is to learn the real target distribution ![]() . To enable generating different targets stochastically, the goal usually becomes to learn the transformation from an initial random distribution
. To enable generating different targets stochastically, the goal usually becomes to learn the transformation from an initial random distribution ![]() (e.g., Gaussian) the real data distribution
(e.g., Gaussian) the real data distribution ![]() .
.
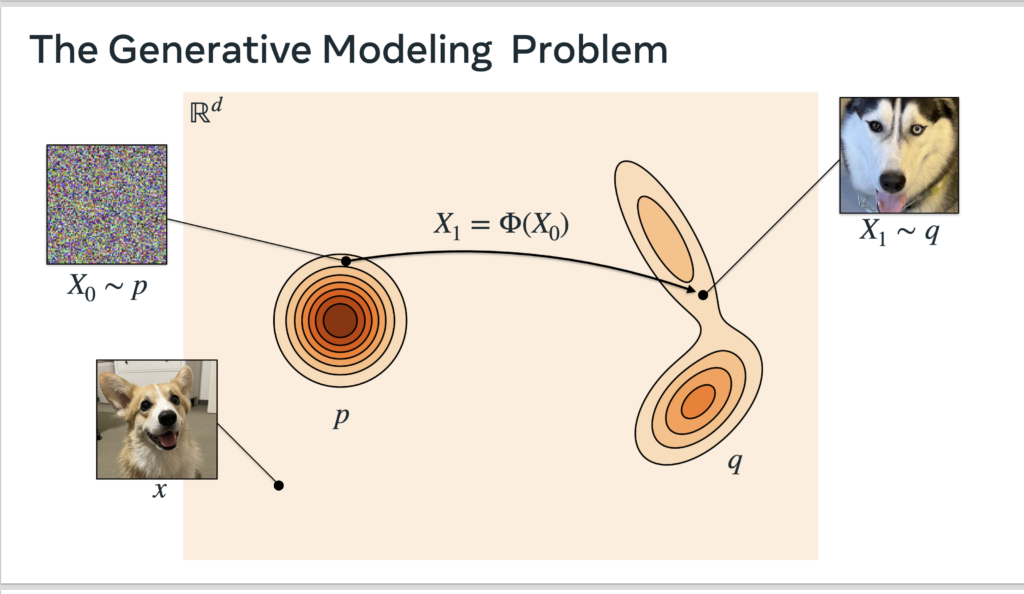
A straightforward method is GAN [5]. However, GAN faces various training instability issues and cannot give the likelihood of a data point, while Flow Matching can address both pain points.
Ordinary Differential Equations (ODE)
ODE describes how a system changes over time. An ODE is defined as:
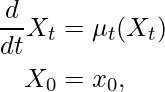
where ![]() . In natural language, we say that
. In natural language, we say that ![]() is a variable representing any point in the
is a variable representing any point in the ![]() -dimensional system at time
-dimensional system at time ![]() , where each dimension is between 0 and 1. At a given time
, where each dimension is between 0 and 1. At a given time ![]() (
(![]() is also between 0 and 1),
is also between 0 and 1), ![]() should move in the direction of
should move in the direction of ![]() , which we call the velocity.
, which we call the velocity. ![]() is also a
is also a ![]() -dimensional vector. The solution of an ODE is called flow,
-dimensional vector. The solution of an ODE is called flow, ![]() , which tells you where an initial point will be at time
, which tells you where an initial point will be at time ![]() . Hence
. Hence ![]() ‘s input is an
‘s input is an ![]() -dimensional point and output is also an
-dimensional point and output is also an ![]() -dimensional point. The ODE above can be rewritten with
-dimensional point. The ODE above can be rewritten with ![]() :
:
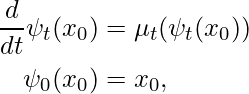
The example below shows how a system moves – the red square grid is the flow, describing each initial point’s “landing” point at time ![]() , and the blue arrow is the velocity at time
, and the blue arrow is the velocity at time ![]() .
.
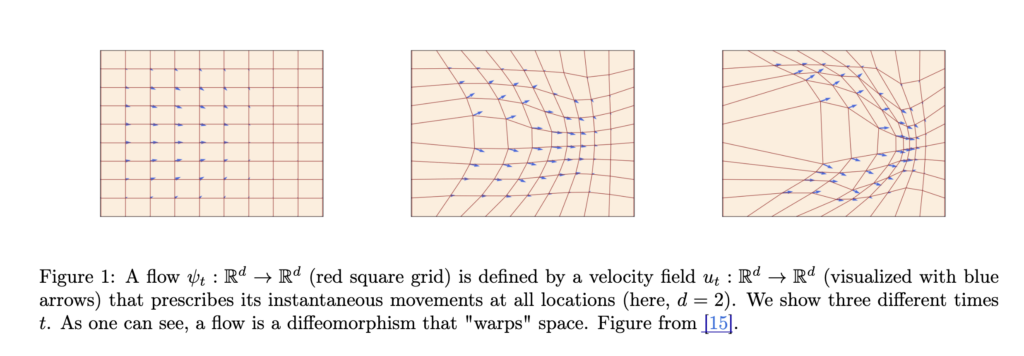 The goal of flow matching is to learn a velocity function
The goal of flow matching is to learn a velocity function ![]() such that
such that ![]() and
and ![]() . With a known/learned velocity function, you can easily simulate how the system changes, which is equivalent to the flow function
. With a known/learned velocity function, you can easily simulate how the system changes, which is equivalent to the flow function ![]() :
:

Conditional / Marginal Probability Path, Conditional and Marginal Velocity Fields
This section is the most mathematical-heavy one. We first introduce the concept of conditional probability path, ![]() . In natural language,
. In natural language, ![]() means the distribution of the position of a point at time
means the distribution of the position of a point at time ![]() if that point starts from
if that point starts from ![]() at time 0 and ends at exactly
at time 0 and ends at exactly ![]() (i.e., a delta distribution at
(i.e., a delta distribution at ![]() ) at time 1, where
) at time 1, where ![]() is any data sampled from the target distribution
is any data sampled from the target distribution ![]() . Therefore, the marginal probability path
. Therefore, the marginal probability path ![]() can be described as:
can be described as:
![]() .
.
![]() simply describes the position distribution of the whole system at time
simply describes the position distribution of the whole system at time ![]() , given the initial distribution is
, given the initial distribution is ![]() and the end distribution is
and the end distribution is ![]() .
.
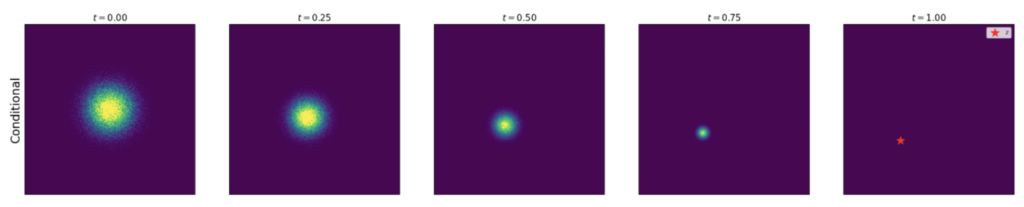
The diagram below describes an example of conditional probability path ![]() : it starts from a 2D gaussian distribution and ends at a particular position marked by the red dot.
: it starts from a 2D gaussian distribution and ends at a particular position marked by the red dot.
The diagram below describes an example of marginal probability path ![]() : it starts from a 2D gaussian distribution and ends at a chessboard-patterned distribution.
: it starts from a 2D gaussian distribution and ends at a chessboard-patterned distribution.

Deriving from the concepts of conditional/marginal probability path, we can also have conditional and marginal velocity field, defined as:
Conditional velocity field: ![]()
Marginal velocity field: ![]()
The formula of marginal velocity field needs a bit work to be proved. We use the rest of this section to prove that.
First, we introduce a theorem called Continuity Equation:
 where the divergence operator is defined as:
where the divergence operator is defined as:
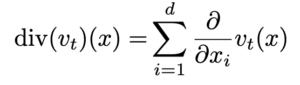
In natural language, this equation says that the change of marginal probability path w.r.t. time is equal to the negative divergence of ![]() . The same theorem can also be applied to the conditional probability path:
. The same theorem can also be applied to the conditional probability path: ![]() .
.
Now we can show that:
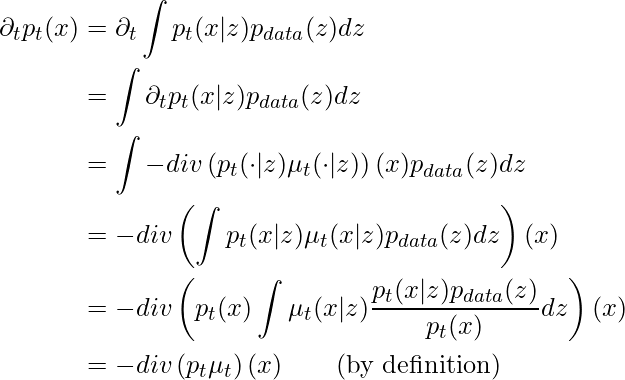
By the last two equations, we proved the relationship between the marginal and conditional velocity fields: ![]()
Training a Practical Flow Matching model
To reiterate the motivation of flow matching: our goal is to learn a velocity function ![]() such that
such that ![]() and
and ![]() . Therefore, the ultimate goal should be:
. Therefore, the ultimate goal should be:
![Rendered by QuickLaTeX.com \mathcal{L}_{FM}(\theta) = \mathbb{E}_{t\sim Unif[0,1], x\sim p_t} \left[ \left\Vert \mu_t^\theta(x)-\mu_t(x) \right\Vert^2 \right] = \mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(x)-\mu_t(x) \right\Vert^2 \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-8d442e13a50791c6da29960192c9f0db_l3.png)
Recall in the section above that ![]() , which involves an integration operator and thus is intractable. Interestingly, we can prove that
, which involves an integration operator and thus is intractable. Interestingly, we can prove that ![Rendered by QuickLaTeX.com \mathcal{L}_{FM}(\theta)=\mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(x)-\mu_t(x) \right\Vert^2 \right] = \mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(x)-\mu_t(x|z) \right\Vert^2 \right] = \mathcal{L}_{CFM}(\theta)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-1e72627ef5ceb9eb41cd75389f19eec3_l3.png) . Therefore, we can explicitly regress our parameterized velocity function against a tractable conditional vector field. This proof can be found in Theorem 18 in [4].
. Therefore, we can explicitly regress our parameterized velocity function against a tractable conditional vector field. This proof can be found in Theorem 18 in [4].
The exact form of ![]() depends on what family of probability path we choose. One particularly popular probability path is the Gaussian probability path. We can define
depends on what family of probability path we choose. One particularly popular probability path is the Gaussian probability path. We can define ![]() and
and ![]() to be two continuously differentiable, monotonic functions with
to be two continuously differentiable, monotonic functions with ![]() and
and ![]() . We can verify that the conditional Gaussian probability path parameterized by
. We can verify that the conditional Gaussian probability path parameterized by ![]() and
and ![]() ,
, ![]() , satisfies the definition of a conditional probability path: at time 0,
, satisfies the definition of a conditional probability path: at time 0, ![]() and
and ![]() . Note that, with the Gaussian conditional probability path, we can simulate the position of
. Note that, with the Gaussian conditional probability path, we can simulate the position of ![]() :
: ![]() , where
, where ![]() . We can then prove that
. We can then prove that ![]() (see detailed proof in Example 11 in [4]).
(see detailed proof in Example 11 in [4]).
With all these intermediate artifacts, we can derive the loss function:
![Rendered by QuickLaTeX.com \begin{align*} \mathcal{L}_{CFM}(\theta) &= \mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(x)-\mu_t(x|z) \right\Vert^2 \right] \\ &= \mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(x)-\left(\dot{\alpha_t}-\frac{\dot{\beta_t}}{\beta_t}\alpha_t \right)z - \frac{\dot{\beta_t}}{\beta_t}x \right\Vert^2 \right] \\ &(\text{let } x=\alpha_t z + \beta_t \epsilon) \\ &= \mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(\alpha_t z + \beta_t \epsilon) - (\dot{\alpha_t} z + \dot{\beta_t} \epsilon) \right\Vert^2 \right] &(\text{special case: } alpha_t=t, \beta_t=1-t) \\ &=\mathbb{E}_{t\sim Unif[0,1], z\sim p_{data}, x\sim p_t(\cdot|z)} \left[ \left\Vert \mu_t^\theta(tz+(1-t)\epsilon) - (z- \epsilon) \right\Vert^2 \right] \end{align*}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-6d2afce51e8290a674829c7bfe31e112_l3.png)
References
[1] https://czxttkl.com/2021/11/15/normalizing-flows/
[2] https://medium.com/@noraveshfarshad/flow-matching-and-normalizing-flows-49c0b06b2966
[3] https://neurips.cc/virtual/2024/tutorial/99531
[4] https://diffusion.csail.mit.edu/docs/lecture-notes.pdf
[5] https://czxttkl.com/2020/12/24/gan-generative-adversarial-network/
[6] https://mlg.eng.cam.ac.uk/blog/2024/01/20/flow-matching.html

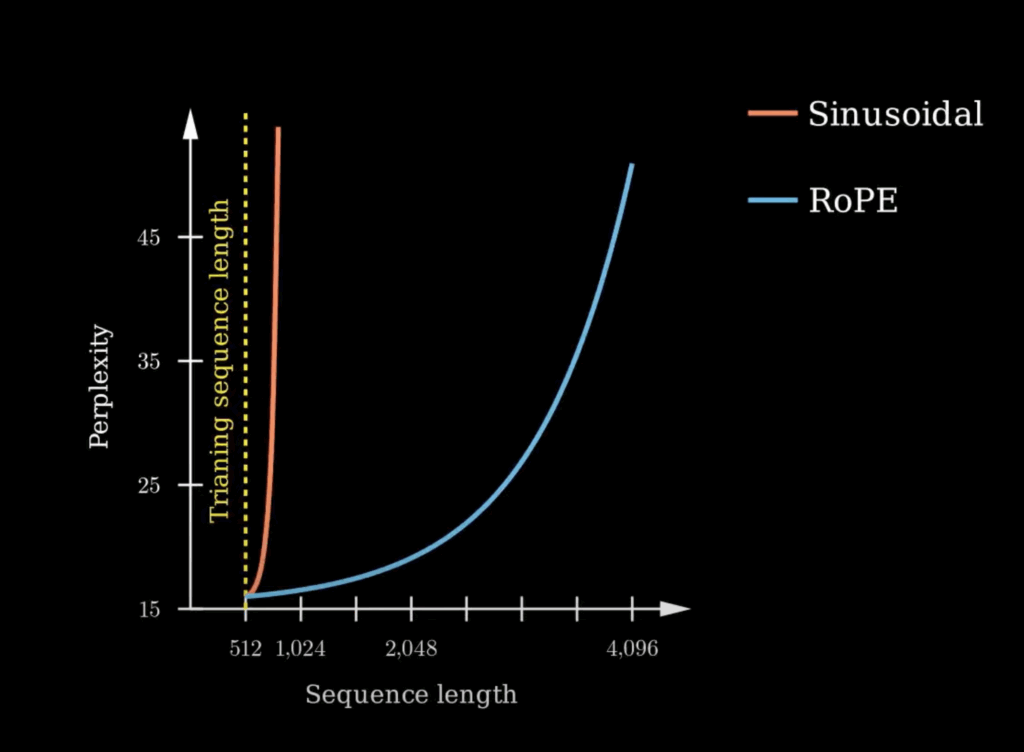
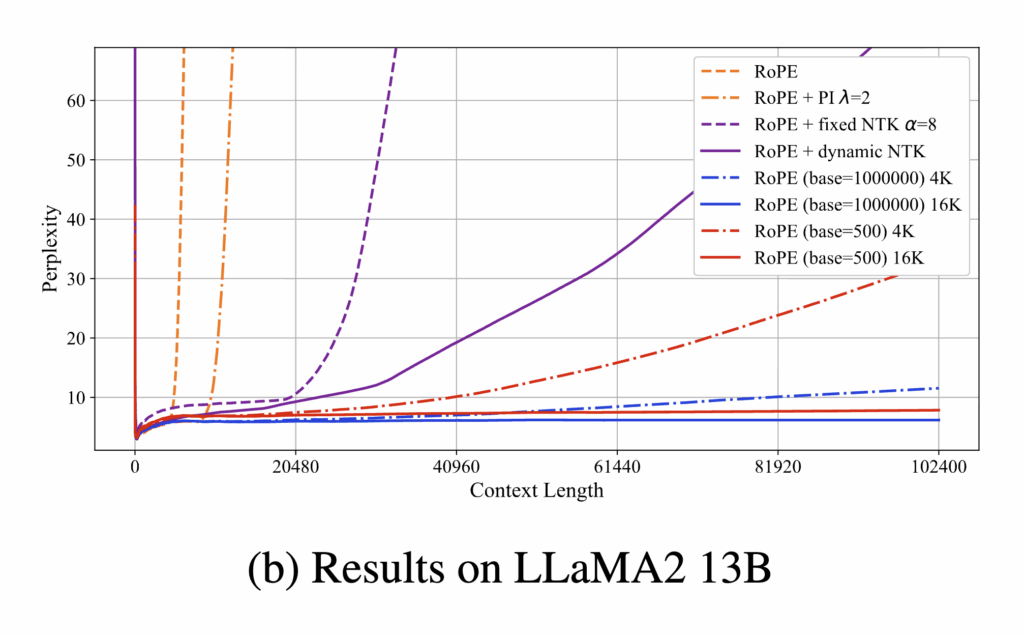
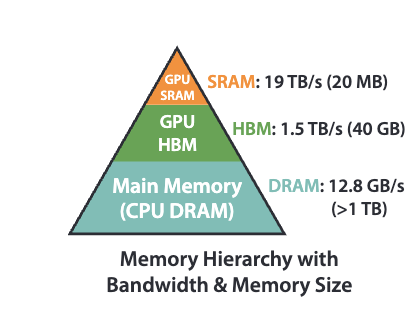 In standard self-attention, it requires
In standard self-attention, it requires 
 Let’s dive into the step of computing softmax. Even computing softmax has many details. First, in real world, we usually need to compute a safe softmax version, where we subtract each input to the softmax with the maximum input to avoid potential overflow. (Diagrams from [3])
Let’s dive into the step of computing softmax. Even computing softmax has many details. First, in real world, we usually need to compute a safe softmax version, where we subtract each input to the softmax with the maximum input to avoid potential overflow. (Diagrams from [3])  In its vanilla implementation, we need to have three passes: the first pass computes the maximum of the input, the second pass computes the denominator of the softmax, and the third pass computes the actual softmax. Asymptotically these three steps require
In its vanilla implementation, we need to have three passes: the first pass computes the maximum of the input, the second pass computes the denominator of the softmax, and the third pass computes the actual softmax. Asymptotically these three steps require  With this 2-pass online softmax algorithm, self-attention can also be computed in two-passes:
With this 2-pass online softmax algorithm, self-attention can also be computed in two-passes:  However, we can do better by finding that
However, we can do better by finding that  That’s how we end up with FlashAttention which requires one pass to compute the output vectors!
That’s how we end up with FlashAttention which requires one pass to compute the output vectors!  In reality, a further optimization is to load Q/K/V in blocks so that the blocks of Q, K, V, and O can occupy roughly the full SRAM memory at one time. That’s why we see block size is set at
In reality, a further optimization is to load Q/K/V in blocks so that the blocks of Q, K, V, and O can occupy roughly the full SRAM memory at one time. That’s why we see block size is set at 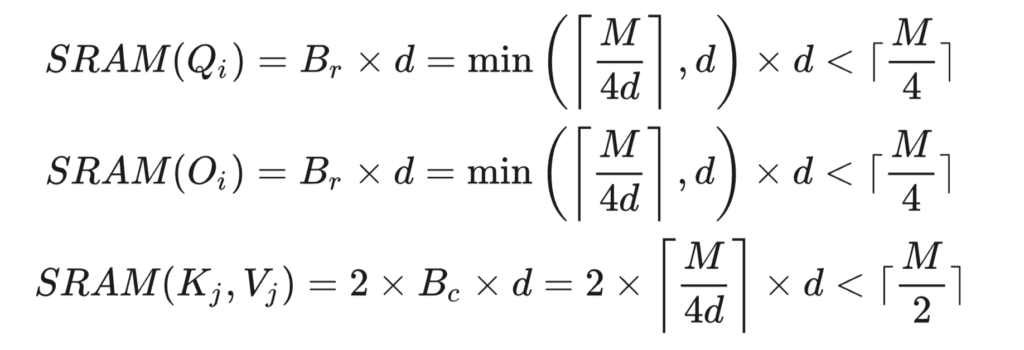 Now, we examine how to do backward computation in FlashAttention. We start from examining the standard attention backward pass:
Now, we examine how to do backward computation in FlashAttention. We start from examining the standard attention backward pass: 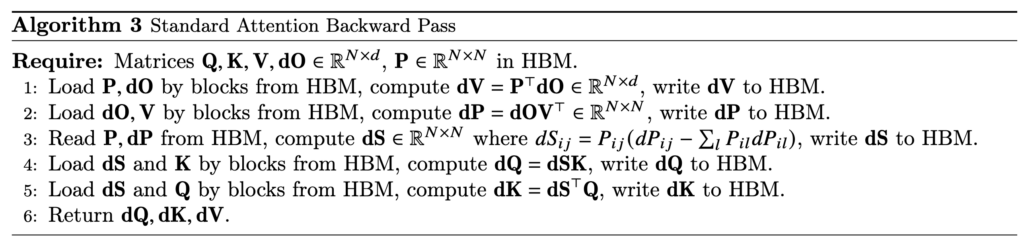 (To clarify the notations,
(To clarify the notations, 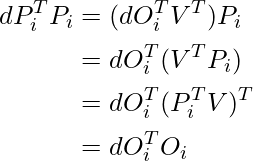
 Let’s also summarize the total memory footprint required by standard attention vs FlashAttention: 1. standard attention: it needs to store
Let’s also summarize the total memory footprint required by standard attention vs FlashAttention: 1. standard attention: it needs to store 








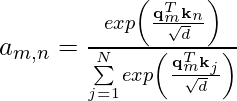
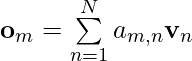

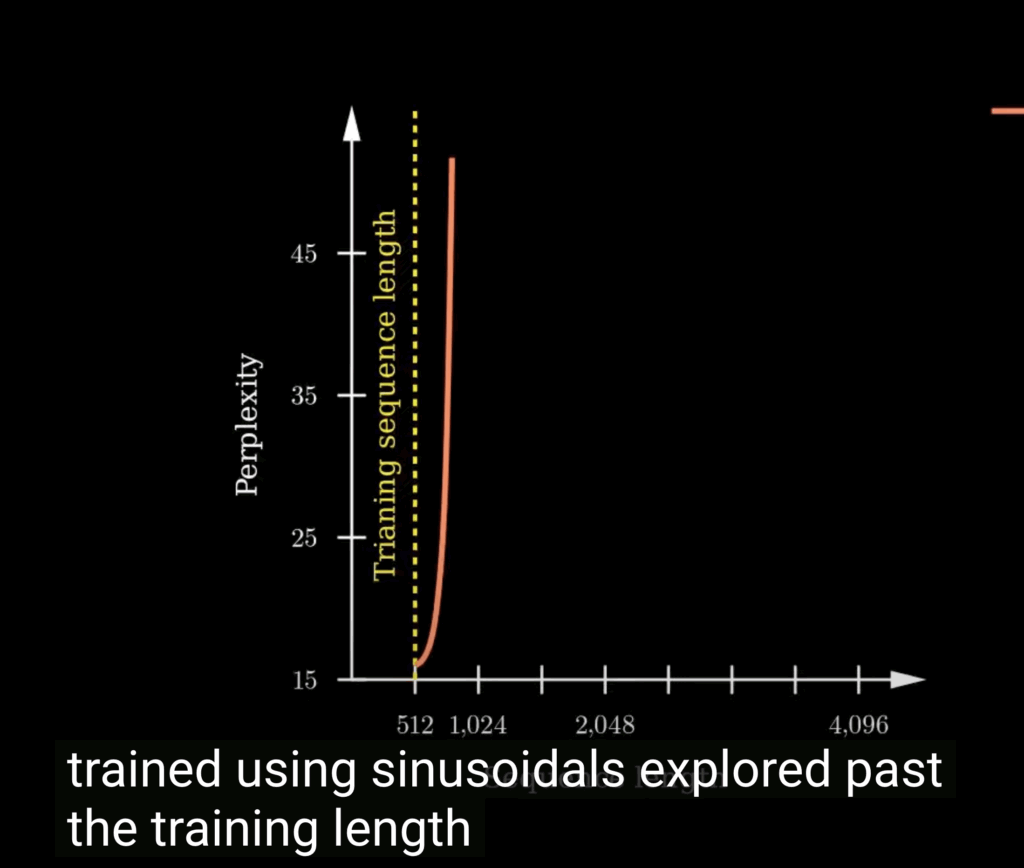
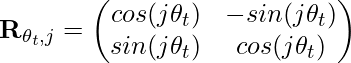
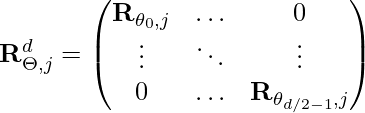

![Rendered by QuickLaTeX.com \mathbf{q}_t^T \mathbf{k}_s = \left(\mathbf{R}^{d}_{\Theta, t} \mathbf{W}_q \mathbf{x}_t \right)^T \left(\mathbf{R}^{d}_{\Theta, s} \mathbf{W}_k \mathbf{x}_s \right) \newline\qquad =\mathbf{x}^T_t \mathbf{W}_q \mathbf{R}^{d}_{\Theta, t-s} \mathbf{W}_k \mathbf{x}_s \newline\qquad = Re\left[\sum\limits_{i=0}^{d/2-1} \mathbf{q}_{[2i:2i+1]} \mathbf{k}^*_{[2i:2i+1]} e^{i(t-s)\theta_{i}} \right]\newline \qquad \text{decrease as t-s increases}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-d94c4f09c13f52eb6323ff2ef3d152a1_l3.png)



![Rendered by QuickLaTeX.com log p_\theta(x) \geq - KL\left(q_\phi(z|x) \Vert p_\theta(x, z)\right) = \newline \mathbb{E}_{z\sim q_\phi(z|x)}\left[ log p_\theta(x|z)\right] - KL\left( q_\phi(z|x) \Vert p(z) \right)](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-c4e9ded405df8f5d13f8a29d89cb7445_l3.png) ,
,
![Rendered by QuickLaTeX.com \text{minimize} \qquad I(z;u) \newline \text{subject to} \quad \mathbb{E}_{z \sim F_{\psi}(z|\mu)}\left[ V^{\pi_\theta^{task}}(z;\mu)\right]=V^*(\mu) \text{ for all } \mu](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-d4f0b6a04603baee6f6cffcd0c405b09_l3.png)










![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) - \beta (\log \pi_\theta(y|x) - \log \pi_{ref}(y|x)) \right] \newline = \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) + \beta \log \pi_{ref}(y|x) - \beta \log \pi_\theta(y|x) \right] \newline \text{because }-\log \pi_\theta(y|x) \text{ is an unbiased estimator of entropy } \mathcal{H}(\pi_\theta)=-\sum_y \pi_\theta(y|x) \log \pi_\theta(y|x), \newline \text{we can transform to equation 2 in [3]} \newline= \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) + \beta \log \pi_{ref}(y|x) + \beta \mathcal{H}(\pi_\theta)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-a33dea15a8c89bf3260776df1cf4d7be_l3.png)
![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) - \beta (\log \pi_\theta(y|x) - \log \pi_{ref}(y|x)) \right] \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} - \frac{1}{\beta}r_\phi(x,y) \right] \newline =\min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} - \log exp\left(\frac{1}{\beta}r_\phi(x,y)\right) \right] \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right)} \right] \newline \pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right) \text{ may not be a valid distribution. But we can define a valid distribution:} \pi^*(y|x)=\frac{1}{Z(x)}\pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right), \text{ where } Z(x) \text{ is a partition function not depending on } y \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi^*(y|x)} \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-abe10cca2808da4aaf2d3f96b11abd12_l3.png)
![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[\underbrace{r_\phi(x,y) + \beta \log \pi_{ref}(y|x)}_{\text{actual reward function}} + \beta \mathcal{H}(\pi_\theta)\right] \newline s.t. \quad \sum\limits_y \pi_\theta(y|x)=1,](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-806a96f47b9f83798b88f60131252bf1_l3.png)

![Rendered by QuickLaTeX.com -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[\log \sigma \left(r(x, y_w) - r(x, y_l)\right) \right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \left(\beta \log \pi^*_\theta(y_w|x) - \beta \log \pi_{ref} (y_w | x) \right) - \left( \beta \log \pi^*_\theta(y_l |x) - \beta \log \pi_{ref} (y_l | x) \right)\right)\right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \beta \log \frac{\pi^*_\theta(y_w|x)}{\pi_{ref} (y_w | x)} - \beta \log \frac{\pi^*_\theta(y_l |x)}{\pi_{ref} (y_l | x)} \right) \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-f305d09d3d4969371cc4d16552d0e9fe_l3.png)
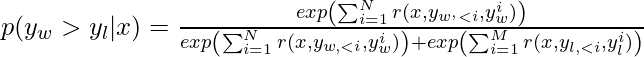
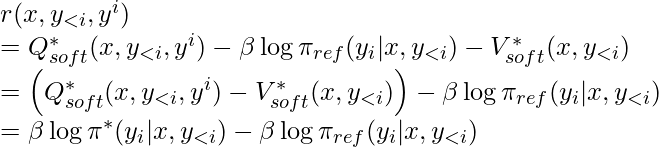
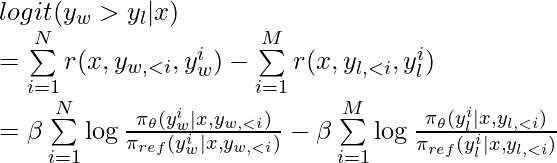
![Rendered by QuickLaTeX.com -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left(\beta \sum\limits_{i=1}^{N}\log \frac{\pi_\theta(y_w^i | x, y_{w, <i})}{\pi_{ref}(y_w^i | x, y_{w,<i})} - \beta \sum\limits_{i=1}^M \log \frac{\pi_\theta(y_l^i | x, y_{l, <i})}{\pi_{ref}(y_l^i | x, y_{l,<i})} \right) \right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \beta \log \frac{\pi^*_\theta(y_w|x)}{\pi_{ref} (y_w | x)} - \beta \log \frac{\pi^*_\theta(y_l |x)}{\pi_{ref} (y_l | x)} \right) \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-982b48b23d236150e21ff1c8f0e9f051_l3.png)