We talked about control variate in [4]: when evaluating ![]() by Monte Carlo samples, we can instead evaluate
by Monte Carlo samples, we can instead evaluate ![]() with
with ![]() in order to reduce variance. The requirement for control variate to work is that
in order to reduce variance. The requirement for control variate to work is that ![]() is correlated with
is correlated with ![]() and the mean of
and the mean of ![]() is known.
is known.
In this post we will walk through a classic example of using control variate, in which ![]() is picked as the Taylor expansion of
is picked as the Taylor expansion of ![]() . We know that
. We know that ![]() ‘s Taylor expansion can be expressed as
‘s Taylor expansion can be expressed as ![]() . Therefore, if we pick the second order of Taylor expansion for
. Therefore, if we pick the second order of Taylor expansion for ![]() and set
and set ![]() , we get
, we get ![]() .
.
Let’s see an example from [6]. Suppose ![]() and we want to evaluate the integral
and we want to evaluate the integral ![]() . If we want to use Monte Carlo estimator to estimate
. If we want to use Monte Carlo estimator to estimate ![]() using
using ![]() samples, we have:
samples, we have: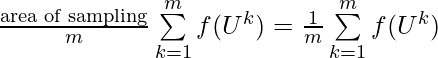
The control variate as the second-order Taylor expansion of ![]() is
is ![]() (we use multi-variable Taylor expansion here [7]). We first compute its mean:
(we use multi-variable Taylor expansion here [7]). We first compute its mean: ![]() . Thus, our control variate Monto Carlo estimator is:
. Thus, our control variate Monto Carlo estimator is:![Rendered by QuickLaTeX.com \frac{1}{m}\sum\limits_{k=1}^{m} z(u_1, u_2)\newline=\frac{1}{m}\sum\limits_{k=1}^{m} \left[f(u_1, u_2) -h(u_1, u_2) + \theta\right]\newline=\frac{1}{m}\sum\limits_{k=1}^{m} \left[exp[(u_1^2 + u_2^2)/2] - 1 - (u_1^2 + u_2^2)/2 + 4/3 \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-cefe400b6090655af28e4c28735815f6_l3.png) .
.
And from the results of [6] the sampling variance of ![]() is smaller than
is smaller than ![]() .
.
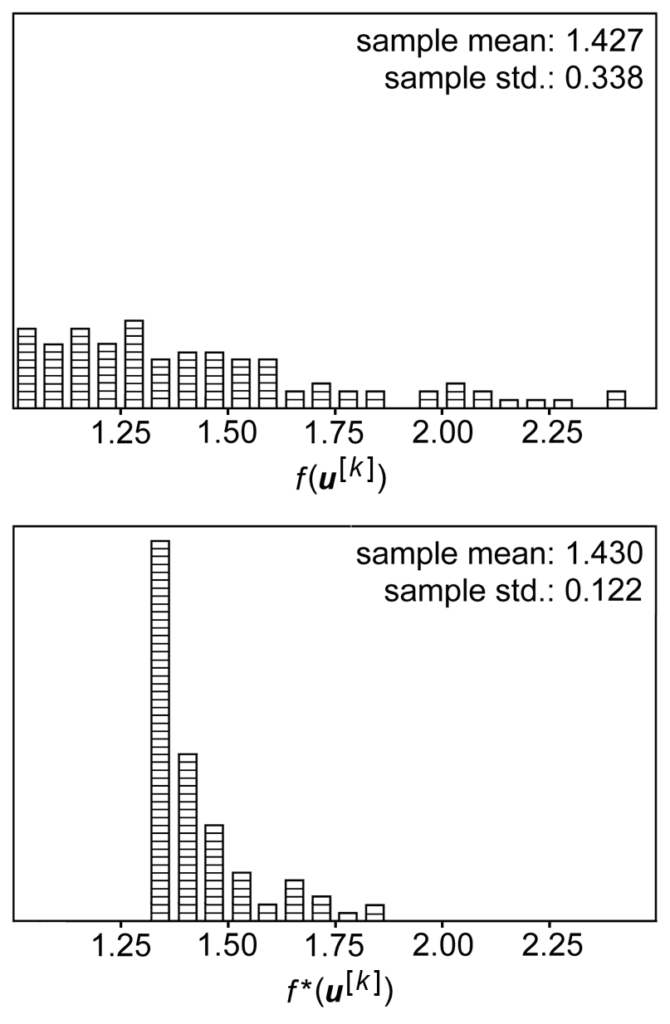
Now what [2] propose is to apply similar Taylor expansion-based control variate on REINFORCE policy gradient:
![]()
If we use Monte Carlo estimator, then we essentially use samples ![]() to approximate
to approximate ![]() , which causes variance. If we have a control variate
, which causes variance. If we have a control variate ![]() and
and ![]() can be chosen at any value but a sensible choice being
can be chosen at any value but a sensible choice being ![]() , a deterministic version of
, a deterministic version of ![]() , then the control variate version of policy gradient can be written as (Eqn. 7 in [2]):
, then the control variate version of policy gradient can be written as (Eqn. 7 in [2]):![Rendered by QuickLaTeX.com \nabla_\theta log \pi_\theta(a_t | s_t) R_t - h(s_t, a_t) + \mathbb{E}_{s\sim \rho_\pi, a \sim \pi}\left[ h(s_t, a_t)\right] \newline=\nabla_\theta log \pi_\theta(a_t | s_t) R_t - h(s_t, a_t) + \mathbb{E}_{s \sim \rho_\pi}\left[ \nabla_a Q_w(s_t, a)|_{a=\mu_\theta(s_t)} \nabla_\theta \mu_\theta(s_t)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9629b8ff4fc66089624196ff0d65190c_l3.png)
As you can see the second term can be computed when ![]() is some critic with known analytic expression, and actually does not depend on
is some critic with known analytic expression, and actually does not depend on ![]() .
.
[3] uses the law of total variance (some good examples and intuitions [8, 9]) to decompose the control-variate policy gradient into three parts: variance caused by variance of states ![]() , variance of actions
, variance of actions ![]() , and variance of trajectories
, and variance of trajectories ![]() . What [3] highlights is that the magnitude of
. What [3] highlights is that the magnitude of ![]() is usually greatly smaller than the rest two so the benefit of using control variate-based policy gradient is very limited.
is usually greatly smaller than the rest two so the benefit of using control variate-based policy gradient is very limited.
References
[1] MUPROP: UNBIASED BACKPROPAGATION FOR STOCHASTIC NEURAL NETWORKS
[2] Q-PROP: SAMPLE-EFFICIENT POLICY GRADIENT WITH AN OFF-POLICY CRITIC
[3] The Mirage of Action-Dependent Baselines in Reinforcement Learning
[4] https://czxttkl.com/2020/03/31/control-variate/
[5] https://czxttkl.com/2017/03/30/importance-sampling/
[6] https://www.value-at-risk.net/variance-reduction-with-control-variates-monte-carlo-simulation/
[7] https://en.wikipedia.org/wiki/Taylor_series#Taylor_series_in_several_variables
[8] http://home.cc.umanitoba.ca/~farhadi/ASPER/Law%20of%20Total%20Variance.pdf