czxttkl

I have always had some doubts on grid search. I am not sure how I should conduct grid search for hyperparameter tuning for a model and report the model’s generalization performance for a scientific paper.

There are three possible ways:

1)  Split data into 10 folds. Repeat 10 times of the following: pick 9 folds as training data, train a model with a specific set of hyperparameters on the training data, test it on the remaining fold and record the test accuracy. Finally, pick the set of hyperparameters achieving the highest mean test accuracy and report that mean test accuracy. 

This procedure is deployed in scikit learn GridSearchCV and also in a cross validated post (note that this post claimed to implement a nested cross validation but I think it is not). But the problem is that the accuracy you finally report is not based on unseen data (as pointed out by https://datascience.stackexchange.com/questions/21877/how-to-use-the-output-of-gridsearch “This goes against the principles of not using test data!!” part). This procedure is also claimed as flawed in another cross validated post: https://stats.stackexchange.com/questions/224287/cross-validation-misuse-reporting-performance-for-the-best-hyperparameter-value?noredirect=1&lq=1

2) Separate out a subset of data as test data. Use the remaining data to pick the best set of hyperparameters as in 1). Then, retrain the model with the best set of hyperparameters on all the data except the test data. Finally, report the accuracy of the retrained model on the test data.

The problem of this method is that the test data is only a small portion of the whole dataset and is tested only once. So the accuracy on the test data may have large variance.

3) Use nested cross validation: http://scikit-learn.org/stable/auto_examples/model_selection/plot_nested_cross_validation_iris.html. Split data into 10 folds. Repeat 10 times of the following: pick 9 folds as a dataset, apply 1) to pick the best set of hyperparameters, retrain a new model on the dataset based on the best set of hyperparameters, and test the retrained model on the remaining fold to obtain an accuracy. Finally, report the mean accuracy across 10 times. This essentially involves two cross validations, often called inner cross validation (for picking the best hyperparameters) and outer cross validation (for reporting the mean accuracy as the generalization error).

The problem of this method is that in each time, you might end up with a different set of hyperparameters. So the mean accuracy reported finally is not guaranteed to average over the models of the same set of hyperparameters.

Based on my research on cross validated forum, 3) is the most correct way. If you end up with the best model with the same set of hyperparameters across 10 times, then that’s perfect since you can just ultimately retrain a model based on the whole dataset with that consistent set of hyperparameters (if you use the scikit learn script given above for nested cross validation, you get the final model by setting refit=True: https://stats.stackexchange.com/a/281824/80635). If you get models with different hyperparameters in each time, that means your model training is not stable, and picking any model of the 10 models is not fair. In this case, either collect more data or debug your model training process until models become stable across 10 times.

Some useful links to help understand:

from https://stats.stackexchange.com/a/72324/80635:

https://stats.stackexchange.com/questions/251752/model-selection-problem-using-nested-cross-validation-in-presence-of-several-alt?rq=1

https://www.elderresearch.com/blog/nested-cross-validation

https://stats.stackexchange.com/questions/65128/nested-cross-validation-for-model-selection

 

Now, I’d like to share one paragraph I used to write in my paper submission:

It is different than 3) in that in each outer cross validation, hyperparameter selection is only based on one shot of training and validation (i.e., there is no inner cross validation).

I have also seen many papers just splitting the whole dataset into training/validation/test set. So this procedure just removes outer cross validation as well. I think people won’t complain about it if the dataset is very large.

At last, I want to share a famous paper, if you have not read it, Random Search for Hyper-Parameter Optimization, which claims that random search can do as well as grid search in many practical problems. llustration can be found here: https://stats.stackexchange.com/questions/160479/practical-hyperparameter-optimization-random-vs-grid-search

Monte Carlo Tree Search (MCTS) has been successfully applied in complex games such as Go [1]. In this post, I am going to introduce some basic concepts of MCTS and its application.

MCTS is a method for finding optimal decisions in a given domain by taking random samples in the decision space and building a search tree according to the results. Search trees are built to gradually cover the search space and in an iterative fashion:

and may result into asymmetric structure:

Each iteration is grouped by four phases, selection, expansion, simulation and backpropagation [4]:

The tree policy and default policy may be defined differently in variations of MCTS. However they all rest on two fundamental concepts: the true value of an action may be approximated using random simulation; and that these values may be used efficiently to adjust the policy towards a best-first strategy [4].

One most widely used variation of MCTS is UCT (Upper Confidence Bounds for Trees), whose tree policy is to select leaf nodes according to a multi-armed bandit metric called UCB1. The pseudo-code is given by [4]:

MCTS’s recent application in Go actually come from three papers [1] (AlphaGo), [2] (AlphaGo Zero), and [9] (AlphaZero). Let’s look at the first paper first [1], in which there are several networks trained:

1) a supervised learning policy network . This is a straightforward, as its input is the board state (plus some move history and human engineered features) and its output is the action to take. The training data is essentially state-action pairs sampled from real human play matches. The goal of this supervised learning policy network is to accurately predict moves. Therefore, it is designed with convoluted structures with 13 layers. As reported, it can achieve 55.7% accuracy and takes 3ms per prediction.

2) a fast supervised learning policy network , which results in simpler structure, faster prediction time but less accuracy. It requires 2us per prediction and has 24.2% accuracy reportedly.

3) a policy network trained based on the supervised learning policy network and by Reinforcement Learning (more specifically, policy gradient method [3]). I think this is a smart choice: if you train a policy network by RL from scratch you may not end up learning well because the game is too complex such that the network will take long time until it adjusts its weights to some meaningful values. Initializing the weights of to is like an effective bootstrapping. On the other hand, ‘s goal is simply achieving prediction accuracy as high as possible, rather than our real goal for winning. The RL-based policy network would adjust the network to fully align with the goal of winning. Thus, a trained should perform stronger than .

4) a value network which estimates the expected outcome from position played by using the RL policy network for both players: . As the paper [1] stated, the most useful value network should estimate the expected outcome under perfect play, , which means each of the two players acts optimally to maximize his own winning probability. But since we do not have perfect play as ground truth, we have to use to generate gameplay data. Therefore, we have . But note that, training a value network is not the only way to estimate . We can also use Monte Carlo rollouts to simulate a large number games by using . However it takes much larger computational resource.

After training the four networks, MCTS will base on these networks to select actions by lookahead search. Let’s look at a typical iteration of MCTS in Alphago:

You could think in such way that each node in the search tree maintains two values and :

where is the value of the leaf state after the selection phase in simulation .  combines the estimated outcome from and a roll out outcome using the fast policy network :

Maintaining and is primarily for defining the tree policy, the policy used to navigate nodes in the selection phase. Specifically, at each time step during the selection phase of a simulation, an action is selected according to:

This is a little different than UCB1 (Upper Confidence Bound) used in UCT (Upper Confidence Bounds for Trees), a common version of MCTS that characterizes using UCB1 in the selection phase [4]:

However, both AlphaGo’s MCTS and UCT share the same idea as to model the action choice in the selection phase as a bandit problem. As such, the action values dynamically change according to historically received average rewards, as well as the number of total trials and trials for that action specifically.

In summary, AlphaGo’s MCTS actually only uses two networks ( and ) from the four trained networks (, , , and ). The two networks  and are only used in the leaf evaluation function .

AlphaGo also embodies two principles of reducing the search space in MCTS. First, to reduce the breadth of search, it selectively pick and expand the action nodes based on the action values calculated as a bandit problem. Additionally, in the simulation (evaluation) phase, the rollout uses the fast policy network to sample actions which also reduces the breadth of the search. Second, to reduce the depth of search, it relies on the leaf evaluation function to evaluate the board value (combined with just one roll out, instead of fully relying on a large number of rollouts).

Now, let’s look at the second version AlphaGo, which is called AlphaGo Zero [2]. The most significant change is that AlphaGo Zero does not require any human play data as in AlphaGo to bootstrap itself. AlphaGo Zero gets rid of training multiple networks but only keeps one unified neural network which learns to output two heads: (1) an action probability distribution (, a vector, whose component is ); (2) and outcome value prediction (, a scalar).

The neural network gets initialized with random weights and will be updated in iterations. Self-play data are generated by two Go AI bots which equip the same neural network snapshot. The neural network snapshot is picked periodically as the best performant player seen so far in all previous iterations. Let us denote the picked snapshot as . At each move, an MCTS search is executed based on in the simulation phase. The output of the MCTS search is an action distribution determined by the upper confidence bound for each action: where , the same bound metric as in AlphaGo [1].

When such self-play proceeds to the game end, we store the game outcome and each of the previous MCTS action distributions as a distribution-outcome tuple . These distribution-outcome tuples will serve as the training data for updating the weights of . The full procedure is illustrated below:

The third version, AlphaZero [9], has further differences than AlphaGo Zero:

1. AlphaZero is more general, which can be applied to other different games such as chess and shogi.  It achieves so by supporting evaluating non-binary game outcomes and less exploiting game-specific training tricks.
2. In AlphaGo Zero, self-play games were generated by the selected snap of the best player from previous iterations. In contrast, AlphaZero simply maintains a single neural network that is updated continually. So self-play games are always generated by the latest parameters for this neural network.

MCTS convergence

According to [5,6], in UCT, the failure probability at the root of the tree (i.e., the probability of selecting a suboptimal action) converges to zero at a polynomial rate as the number of games simulated grows to infinity. In a two-person zero-sum game, this means UCT converges to the minimax algorithm’s solution, which is the optimal move if both players are under perfect play, which is also the move to minimize the maximal possible loss the opponent can exert.

Here, I am using a small example to sketch why UCT could converge to minimax. First, the following plot shows a minimax tree for a game. Each of two players makes exactly one move until the game ends. The numbers in the circles indicate the reward to the player. Solid lines indicate the actual moves selected under perfect play by both players.

Now, suppose we start to build a UCT. Since UCT has the exploration term , we could imagine that at some point each terminal state has been visited once:

Here in each circle there is a tuple indicating the average reward and visited times on that node. If MCTS stops at this moment, it seems like the player would choose the right action because it has a higher average reward, which is different than the minimax solution.

However, after that, UCT would traverse the node (-5,1) much more frequently than the node (-50,1). Therefore, The node (27.5, 2) will eventually converge to its real reward 5.

Reference

[1] Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., … & Dieleman, S. (2016). Mastering the game of Go with deep neural networks and tree search. nature, 529(7587), 484-489.

[2]  Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., … & Chen, Y. (2017). Mastering the game of go without human knowledge. Nature, 550(7676), 354.

[3] https://czxttkl.com/?p=2812

[4] Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M., Cowling, P. I., Rohlfshagen, P., … & Colton, S. (2012). A survey of monte carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in games, 4(1), 1-43.

[5] Kocsis, L., Szepesvári, C., & Willemson, J. (2006). Improved monte-carlo search. Univ. Tartu, Estonia, Tech. Rep, 1.

[6] Kocsis, L., & Szepesvári, C. (2006, September). Bandit based monte-carlo planning. In European conference on machine learning (pp. 282-293). Springer, Berlin, Heidelberg.

[9] Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., … & Hassabis, D. (2017). Mastering chess and shogi by self-play with a general reinforcement learning algorithm. 

Cross Entropy (CE) method is a general Monte Carlo method originally proposed to estimate rare-event probabilities but then naturally extended to solve optimization problems. It is relevant to several my previous posts. For example, both Bayesian Optimization [5] and CE method can be used to solve black-box optimization problems, although Bayesian Optimization mostly works on continuous input domains whereas CE mostly works on combinatorial black-box optimization problems, i.e., inputs are discrete. For another example, CE is largely based on importance sampling [1], a variance reduction method whose core idea is, when estimating the expectation of some quantity, sampling its random variables on a different pdf such that the variance of the estimation can be smaller than sampling on the original pdf [6].

In this post, I am going to talk about my understanding in CE method. My understanding largely comes from a great tutorial [2].

Let’s first see how CE works on rare-event probability evaluation. The goal of rare-event probability evaluation is to estimate:

$latex \ell=P(S(\textbf{X}) \geq \gamma) = \mathbb{E} \textit{I}_{\{S(\textbf{X}) \geq \gamma\}},&s=2$

where $latex \textbf{X}$ is a multidimensional random variable vector following a probability density function (pdf) $latex f(\textbf{x};\textbf{u})$, $latex S(\textbf{X})$ is a (possibly black-box) function that returns a quantity for any given $latex \textbf{X}$, $latex \textit{I}(\cdot)$ is an identity function returns 1 if what is inside is true otherwise 0.

[2] notes that the naive way to estimate $latex \ell$ is to use Crude Monte Carlo (CMC) simulation:

The disadvantage is that if $latex S(\textbf{X}) \geq \gamma$ is rare, in other word, $latex \gamma$ is large, positive samples will be scarce. Therefore, CMC may need a lot of time and samples before it returns a reliable estimation.

Therefore, we turn to another technique called importance sampling. In importance sampling, we sample $latex \textbf{X}$ in another distribution $latex g(\textbf{X})$, let’s say $latex g(\textbf{x})=f(\textbf{x}; \textbf{v})$, the same distribution family as $latex f(\textbf{x}; \textbf{u})$ but with different parameters. This converts estimating the expectation of $latex \textit{I}_{\{ S(\textbf{X}) \geq \gamma \}} &s=2$ to estimating the expectation of $latex \textit{I}_{\{ S(\textbf{X})\geq \gamma \}} \frac{f(\textbf{X})}{g(\textbf{X})} &s=2$:

The central idea of importance sampling is that if sampling on $latex g(\textbf{x})=f(\textbf{x}; \textbf{v})$ can make the event $latex S(\textbf{X}) \geq \gamma$ appear more often, and if we know the exact form of $latex g(\textbf{x})$, and provided that we already know the exact form of $latex f(\textbf{x}; \textbf{u})$, then $latex \hat{\ell}$ (Eqn.5) would have smaller variance than Eqn. 3. In other words, we could have needed less samples to estimate $latex \ell$ in the same precision as in CMC. 

In theory, the best $latex g(\textbf{x})$ from the same distribution family of $latex f(\textbf{x};\textbf{u})$ to reduce the estimation variance is:

The obvious difficulty is that we do not know $latex g^*(\textbf{x})$ in advance because we do not know $latex \ell$ in advance. To tackle this, we want to fit a distribution from the same distribution family of $latex f(\textbf{x};\textbf{u})$ as close as possible to approximate $latex g^*(\textbf{x})$. This is achieved by searching for a set of parameters $latex \textbf{v}$ such that the Kullback-Leibler distance (also named cross-entropy) between $latex g^*(\textbf{x})$ and $latex f(\textbf{x};\textbf{v})$ is minimized:

To estimate Eqn. 13 stochastically, we have:

$latex \max_{\textbf{v}} D(\textbf{v}) = \max_{\textbf{v}} \frac{1}{N} \sum\limits_{i=1}^N \textit{I}_{\{S(\textbf{X}_i) \geq \gamma \}} ln(\textbf{X}_i;\textbf{v}) &s=2$,

where $latex \textbf{X}$ is drawn from $latex f(\textbf{x};\textbf{u})$.

 

To this point, we still face the difficulty that the event $latex S(\textbf{X}) \geq \gamma$ happens rarely such that this estimation may have large variance. Therefore, we use importance sampling again and introduce another distribution $latex f(\textbf{x};\textbf{w})$ on Eqn. 13, hoping that $latex f(\textbf{x};\textbf{w})$ can make $latex S(\textbf{X}) \geq \gamma$ appear more often:

 

Now, the most important question is: how can we know $latex \textbf{w}$? After all, if we know $latex \textbf{w}$, the rest of the problem would be just to sample $latex \textbf{X}$ based on $latex f(\textbf{x};\textbf{w})$, and solve Eqn. 15 using Eqn. 16 and Eqn. 17.  

The answer is: we can obtain $latex \textbf{w}$ iteratively. We will also need a sequence $latex \{\gamma_t, t \geq 1\}$. We will start with $latex \textbf{w}_0=\textbf{u}$ and $latex \gamma_1 < \gamma$ such that $latex S(\textbf{X}) \geq \gamma_1$ isn’t too rare if sampling on $latex \textbf{w}_0$. A canonical way is to set $latex \rho=0.01$ and let $latex \gamma_1$ be the $latex (1-\rho)$-quantile of $latex S(X)$ sampling from $latex \textbf{w}_0$. Setting $latex \gamma=\gamma_1$ and $latex \textbf{w}=\textbf{w}_0$ in Eqn. 15, we can obtain $latex \textbf{v}^*_1$. You can think $latex f(\textbf{x}; \textbf{v}^*_1)$ the best distribution to sample for estimating $latex \mathbb{E}_{\textbf{u}} \textit{I}_{\{S(\textbf{X}) \geq \gamma_1 \}} $. More importantly, compared to $latex f(\textbf{x}; \textbf{u})$, sampling from $latex f(\textbf{x};\textbf{v}^*_1)$ makes the event $latex S(\textbf{X}) \geq \gamma$ a little less rare: the probability mass shifts a bit towards the event $latex S(\textbf{X}) \geq \gamma$.

The iteration goes on by setting $latex \textbf{w}_1=\textbf{v}^*_1$ and $latex \gamma_2$ to be the $latex (1-\rho)$-quantile of $latex S(X)$ sampling from $latex \textbf{w}_1$. Solving Eqn.15 can result to the best distribution $latex f(\textbf{x};\textbf{v}^*_2)$ to sample for estimating $latex \mathbb{E}_{\textbf{u}} \textit{I}_{\{S(\textbf{X}) \geq \gamma_2 \}}$. Again, the probability mass of $latex f(\textbf{x};\textbf{v}^*_2)$ shifts a little bit towards  the event $latex S(\textbf{X}) \geq \gamma$. 

The iterations loop until $latex \gamma_t$ is not less than $latex \gamma$, i.e., sampling $latex \textbf{X}$ from $latex \textbf{w}_t$ sees the event $latex S(\textbf{X}) \geq \gamma$ frequently enough. Until this point, Eqn. 5 can be used reliably to estimate $latex \ell$.

The full version of the algorithm is as follows:

I found it is useful to understand the whole process by using a toy example: $latex \textbf{X}$ is a one-dimension random variable. $latex S(\textbf{X})=\textbf{X}$. $latex f(\textbf{x};\textbf{u})$ is a just a normal distribution. $latex \gamma$ is a relatively large number falling outside the 3 times of the standard deviation of $latex f(\textbf{x};\textbf{u})$.

Obviously, sampling from $latex f(\textbf{x};\textbf{u})$ to estimate $latex \mathbb{E} \textit{I}_{\{S(\textbf{X}) \geq \gamma \}}$ requires a large number of samples. Following Algorithm 3.1, we will set a less rare $latex \gamma_1 < \gamma$ and calculate $latex f(\textbf{x};\textbf{v}^*_1)$.

Keeping doing that will end up with $latex \gamma_t$ and $latex f(\textbf{x};\textbf{v}^*_t)$ shifting closer and closer to $latex \gamma$ until sampling $latex S(\textbf{X}) \geq \gamma$ is no longer too rare under $latex f(\textbf{x};\textbf{v}^*_t)$.

 

To this point, we finish introducing how CE method is applied in rare event probability estimation. Now, we introduce how CE method can be applied in combinatorial search problem. The setting of a typical combinatorial search problem is:

For every combinatorial search problem, we can associate it with a rare-event probability estimation problem: to estimate $latex P_{\textbf{u}}(S(\textbf{X}) \geq \gamma)$. It doesn’t matter how you choose the distribution $latex f(\textbf{x};\textbf{u})$ and $latex \gamma$ for the associated problem, what it matters is the pattern we observe in Algorithm 3.1: both intermediate distribution $latex f(\textbf{x};\textbf{v}^*_t)$ and $latex \gamma_t$ will iteratively shift towards the direction of the maximum of $latex S(\textbf{X})$. If we let the iteration loop long enough, $latex f(\textbf{x};\textbf{v}^*_t)$ and $latex \gamma_t$  will end up around the area of the maximum of $latex S(\textbf{X})$. After that, $latex \gamma_T$ will faithfully be close to $latex \gamma^*$ and sampling from $latex f(\textbf{x};\textbf{v}^*_T)$ will faithfully generate approximated optimal solution. This idea basically shapes Algorithm 3.3:

 

I will wrap up this post here. For more examples using CE method, please review [2] and [3]. 

 

Reference

[1] https://czxttkl.com/?p=2770

[2] http://web.mit.edu/6.454/www/www_fall_2003/gew/CEtutorial.pdf

[3] https://people.smp.uq.edu.au/DirkKroese/ps/CEopt.pdf

[4] https://en.wikipedia.org/wiki/Cross-entropy_method

[5] https://czxttkl.com/?p=3212

[6] https://en.wikipedia.org/wiki/Importance_sampling#Application_to_simulation

 

In this post, I am going to share my understanding in Bayesian Optimization. Bayesian Optimization is closely related Gaussian Process, a probabilistic model explained in details in a textbook called “Gaussian Processes for Machine Learning” [1]. In the following, “p. ” will refer to a specific page in [1] where the content comes from. 

First, let’s dive into the detail of Gaussian Process. 

We need to have a new thinking model in our mind: think any function $latex f(x)$ as a very long vector, each entry in the vector specifying the function value $latex f(x)$ at a particular input $latex x$ (p. 2). Of course, in theory, this vector will be arbitrarily, infinitely long because we can measure $latex f(x)$ at arbitrarily scaled precision. Let’s make it clear that $latex x$ is the input of $latex f(x)$ and it has $latex d$ dimension: $latex x \in \mathbb{R}^d$. Usually, we let $latex x$ be a column vector.

One step further, we need to think the function vector as a vector of random variables. Each entry of the vector is a random variable, meaning that there is a probability distribution for every $latex f(x)$ at a specific $latex x$.  Since they are all random variables, any finite number of the entries can be selected to form a joint probability distribution.

Let $latex X \in \mathbb{R}^{n \times d}$ be the aggregation matrix of $latex x$ corresponding to the picked entries. Let $latex f=\{f(X_{i})\}_{i=1}^n$, a vector of $latex f(x)$ at different $latex x$ in $latex X$. If we assume $latex f(x)$ follows Gaussian Process (p. 13), then the joint probability distribution of $latex f$ (induced by any $latex X$) will be a Gaussian distribution:

$latex f \sim \mathcal{N}(m(X), K(X, K)),&s=2$

where $latex m(X) \in \mathbb{R}^n$ is a mean function vector whose each entry is defined as $latex m(x)=\mathbb{E}[f(x)]$; and $latex K(X, X) \in \mathbb{R}^{n \times n}$ is the covariance matrix of the Gaussian distribution. The entry on $latex p$ row, $latex q$ column, $latex K_{pq}(X, X)$, is defined as a covariance function between $latex x_p$ and $latex x_q$: $latex k(x_p, x_q)=\mathbb{E}[(f(x_p)-m(x_p))(f(x_q)-m(x_q))]$.  

For such $latex f(x)$ following Gaussian Process, we can write as: $latex f(x) \sim \mathcal{GP}(m(x), k(x, x’))$, reading as “$latex f(x)$ follows a Gaussian Process governed by a mean function $latex m(x)$ and a covariance function $latex k(x,x’)$”.

Let’s now look at a Bayesian linear regression model $latex f(x)=\phi(x)^T w$ with $latex \phi(x)$ as a feature transformation function to transform $latex x$ into a high-dimension space and a prior distribution $latex w \sim \mathcal{N}(0, \Sigma_p)$.

For any $latex x$, $latex \mathbb{E}[f(x)] = \phi(x)^T \mathbb{E}[w] = 0$. For any $latex x$ and $latex x’$, $latex \mathbb{E}[(f(x)-m(x))(f(x’)-m(x’))] = \phi(x)^T \mathbb{E}[w w^T]\phi(x’) = \phi(x)^T \Sigma_p \phi(x’)$ (p. 14). Actually, for any finite number of inputs $latex x_1, x_2, \cdots, x_n$, the function values $latex f(x_1), f(x_2), \cdots, f(x_n)$ forms a joint Gaussian distribution with zero means and convariance given as $latex k(x, x’)=\phi(x)^T \Sigma_p \phi(x’)$: $latex f \sim \mathcal{N}(0, K(X, X))$. Therefore, we can say $latex f(x)$ in the Bayesian linear regression model follows a Gaussian Process. 

If we set $latex k(x, x’)=\phi(x)^T \Sigma_p \phi(x’) = exp(-\frac{1}{2}|x – x’|^2)$, then this corresponds $latex \phi(x)$ to transform $latex x$ into an infinite feature space. We call this covariance function squared exponential (SE) or radial basis function (RBF). Please review [2] for kernel methods introduced in SVM.  There of course exist many other covariance functions. Different covariance functions will govern the shape of the joint Gaussian distribution of $latex f$ (and also the conditional distribution of new $latex f$ given observations, which we will talk next). From now on, we will assume we use SE as the covariance function.

Since we have $latex f \sim \mathcal{N}(0, K(X, X))$ as the joint distribution for any finite number of $latex x$, we can draw multivariate samples from the joint distribution. Figure 2.2 (a) (p.15) shows three drawn samples: first, we prepare a series of equidistant $latex x$, say, -5.0, -4.9, -4.8, … 4.8, 4.9, 5.0, which can be aggregated to a matrix $latex X$; then, we draw $latex f(x)$ according to $latex f \sim \mathcal{N}(0, K(X, X))$. By connecting the generated points $latex (x, f(x))$ we get three functions (the red line, the green line, or the dotted blue line). The gray area represents the pointwise mean plus and minus two times the standard deviation for each input value. Because we know $latex m(x)=0$ and $latex k(x,x’)=1$ for all $latex x$, the gray area is actually a rectangle between 2 and -2.

So far we are only dealing with a Gaussian Process prior because we have not observed any data therefore no more information can be utilized. The most interesting part comes as we have some (for now, we assume noiseless) observations $latex \{(x_i, f_i)|i=1,\cdots,n\}$ and we want to extract any insight to make more accurate guess about new the function values at new $latex x$. We will use $latex f$ to denote the observation outputs, and $latex f_*$ for new test outputs. We will use $latex X_*$ to denote the aggregated matrix of test $latex x$. Because $latex f(x)$ follows a Gaussian Process, $latex [f, f_*]$ still forms a joint Gaussian distribution (p.15):

The most important part is that we want to infer future $latex f_*$ based on observed $latex f$. Therefore, we shouldn’t merely look at the joint distribution but instead should focus on the conditional distribution $latex f_*|X_*, X, f$, which can also be called the posterior distribution. It turns out that the posterior distribution is still a Gaussian distribution (p. 16):

Figure 2.2 (b) (p.15) shows three randomly drawn functions obtained in a similar manner as in Figure 2.2 (a) based on the posterior distribution: first, we prepare a series of equidistant $latex x_*$, say, -5.0, -4.9, -4.8, … 4.8, 4.9, 5.0, which can be aggregated to a matrix $latex X_*$; then, we draw $latex f_*$ according to $latex f_*|X_*,X,f$. By connecting the generated points $latex (x_*, f_*)$ we get three functions (the red line, the green line, or the blue line). Note that, the gray area is no longer constant: in the area close to observations, the pointwise standard deviation is small; it is larger in less observation-dense areas indicating less confidence:

In the following chapters of [1], it continues to introduce the situation when our observations are not noise-free. In this situation, the posterior distribution becomes (p. 16):

In the case that there is only one test point $latex x_*$, we write $latex k(x_*)=k_*$ to denote the vector of covariances between the test point and the $latex n$ training points and we have:

So far we’ve derived the posterior distribution from a function space view. What is interesting is that the same posterior distribution can be obtained from a pure probabilistic way (i.e., weight space view), a way we are more familiar with, without thinking functions in a function space. 

It starts from Bayesian Theorem: 

$latex p(w|y,X) = \frac{p(y|X,w)p(w)}{p(y|X)} \propto p(y|X,w) p(w) &s=2$

 

In a Bayesian linear model, we assume $latex y=f(x) + \epsilon$, $latex \epsilon \sim \mathcal{N}(0, \sigma_n^2)$ and $latex w \sim \mathcal{N}(0, \Sigma_p)$. Therefore,

The posterior distribution given observation $latex X$, $latex y$ and new $latex x_*$ becomes (p. 11):

To empower a linear model, we can use a feature transformation $latex \phi(x)$ to transform $latex x$ into a high-dimensional space and apply the linear model in that space: $latex f(x) = \phi(x)^T w$. The posterior distribution changes accordingly (p. 12):

In Eqn. 2.12, the transformed features only enter in the form of $latex \phi_*^T\Sigma_p\phi$, $latex \phi_*^T\Sigma_p\phi_*$ and $latex \phi^T\Sigma_p\phi$. This can be again thought as some form of kernel: $latex k(x,x’)=\phi(x)^T\Sigma_p\phi(x’)$. Therefore, we arrive at the same posterior distribution as in Eqn. 2.22~2.24.

We finished introducing Gaussian Process. Now, we introduce Bayesian Optimization. Bayesian Optimization is mostly used for black-box optimization:

$latex max_x f(x), &s=2$

where the objective function $latex f(x)$ is assumed to have no known analytic expression and expensive to evaluate. The idea is to iteratively make guess about next promising observation based on existing observations until the (approximated) optimum is found [3]. The guess will be based on a constructed acquisition function, which has some closed form and is much cheaper to evaluate than the original objective function. People have proposed many forms of acquisition function. One thing for sure is that they all rely on the posterior distribution $latex f_*|X_*, X, f$. The link between Gaussian Process and Bayesian Optimization is that Bayesian Optimization assumes the black-box function to be maximized follows Gaussian Process thus the posterior distribution $latex f_*|X_*, X, f$ will follow a Gaussian distribution we know how to express analytically.

Intuitively, a good acquisition function should not only favor the area where the posterior mean is high (so it can exploit learned information), but also favor the area with much uncertainly (so that further exploration can be performed). One popular of such acquisition function is called Expected Improvement (EI):

 

where $latex x^+=argmax_{x_i \in x_{1:t}} f(x_i)$. Interpreted this expression in English, it speaks that we want to find the next $latex x$ that has the largest expected improvement of the best $latex x^+$ so far. If we are unsure about $latex f(x)$ at $latex x$, $latex EI(x)$ will also be large.

If we set the pointwise mean and standard deviation of the posterior distribution of $latex f_{t+1}(x)$ as $latex \mu(x)=\bar{f}_*$ and $latex \sigma^2(x)= \mathbb{V}[f_*]$ [See equation 2.25 and 2.26 (p.17)], and if we set a random variable $latex I=\mathbb{E}[max\{0, f_{t+1}(x)-f(x^+)\}]$, we will have:

We’ve known how to compute $latex EI(x)$, the acquisition function. The only remaining question is now how to sample next $latex x$. This remains a practical problem that I will investigate the future. But the whole idea of Bayesian Optimization has been clear now.

 

Reference

[1] http://www.gaussianprocess.org/gpml/

[2] https://czxttkl.com/?p=3114

[3] A Tutorial on Bayesian Optimization of Expensive Cost Functions, with application to Active User Modeling and Hierarchical Reinforcement Learning

[4] Bayesian Optimization with Inequality Constraints

Two informal posts:

[] https://arimo.com/data-science/2016/bayesian-optimization-hyperparameter-tuning/

[] https://thuijskens.github.io/2016/12/29/bayesian-optimisation/

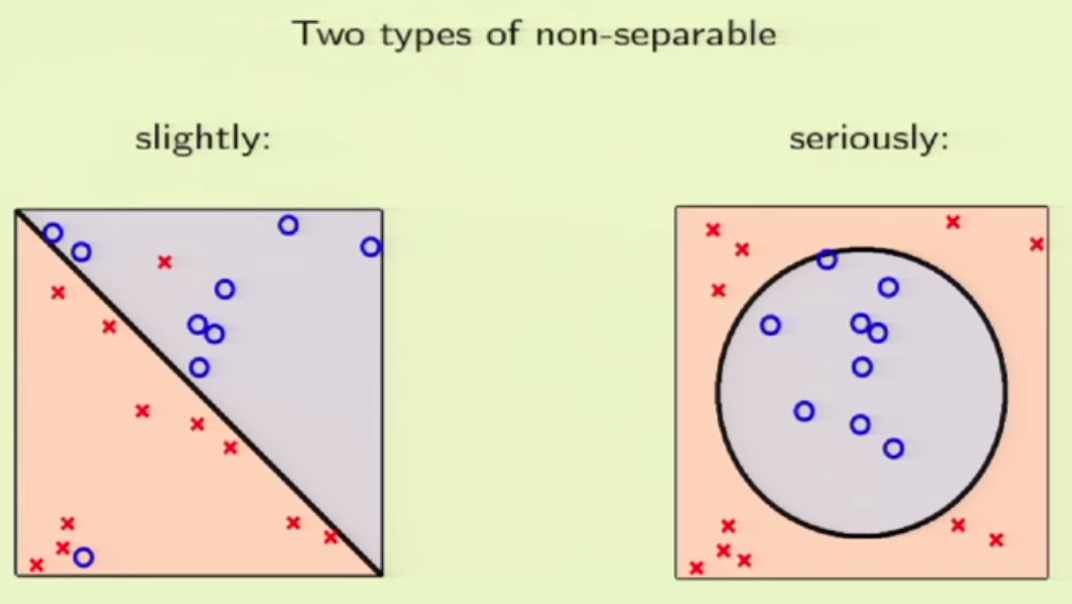
In this post, I am going to walk through an online piece of code [7] which implements the idea of [1]: using pointer network [2] to solve travelling salesman problem. Pointer networks, in my understanding, are neural network architectures for the problems where output sequences come from the permutation of input sequences.

Some background posts you may read in first:

[3]: policy gradient such as REINFORCE

[4]: LSTM code walk through

[5, 6]: travelling salesman problem

The code is based on [7] but modified in several small places to work with python 3.6 and torch 0.3.0 and cuda 8.0. 

import math
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.autograd as autograd
import torch.nn.functional as F
from torch.autograd import Variable
from torch.utils.data import Dataset, DataLoader
from IPython.display import clear_output
from tqdm import tqdm
import matplotlib.pyplot as plt

USE_CUDA = True


class TSPDataset(Dataset):
    def __init__(self, num_nodes, num_samples, random_seed=111):
        super(TSPDataset, self).__init__()
        torch.manual_seed(random_seed)

        self.data_set = []
        for l in tqdm(range(num_samples)):
            x = torch.FloatTensor(2, num_nodes).uniform_(0, 1)
            self.data_set.append(x)

        self.size = len(self.data_set)

    def __len__(self):
        return self.size

    def __getitem__(self, idx):
        return self.data_set[idx]


def reward(sample_solution):
    """
    Args:
        sample_solution seq_len of [batch_size]
    """
    batch_size = sample_solution[0].size(0)
    n = len(sample_solution)
    tour_len = Variable(torch.zeros([batch_size]))

    if USE_CUDA:
        tour_len = tour_len.cuda()

    for i in range(n - 1):
        tour_len += torch.norm(sample_solution[i] - sample_solution[i + 1], dim=1)

    tour_len += torch.norm(sample_solution[n - 1] - sample_solution[0], dim=1)

    return tour_len


class Attention(nn.Module):
    def __init__(self, hidden_size, use_tanh=False, C=10, name='Bahdanau'):
        super(Attention, self).__init__()

        self.use_tanh = use_tanh
        self.C = C
        self.name = name

        if name == 'Bahdanau':
            self.W_query = nn.Linear(hidden_size, hidden_size)
            self.W_ref = nn.Conv1d(hidden_size, hidden_size, 1, 1)

            V = torch.FloatTensor(hidden_size)
            if USE_CUDA:
                V = V.cuda()
            self.V = nn.Parameter(V)
            self.V.data.uniform_(-(1. / math.sqrt(hidden_size)), 1. / math.sqrt(hidden_size))

    def forward(self, query, ref):
        """
        Args:
            query: [batch_size x hidden_size]
            ref:   ]batch_size x seq_len x hidden_size]
        """

        batch_size = ref.size(0)
        seq_len = ref.size(1)

        if self.name == 'Bahdanau':
            ref = ref.permute(0, 2, 1)
            query = self.W_query(query).unsqueeze(2)  # [batch_size x hidden_size x 1]
            ref = self.W_ref(ref)  # [batch_size x hidden_size x seq_len]
            expanded_query = query.repeat(1, 1, seq_len)  # [batch_size x hidden_size x seq_len]
            V = self.V.unsqueeze(0).unsqueeze(0).repeat(batch_size, 1, 1)  # [batch_size x 1 x hidden_size]
            logits = torch.bmm(V, F.tanh(expanded_query + ref)).squeeze(1)

        elif self.name == 'Dot':
            query = query.unsqueeze(2)
            logits = torch.bmm(ref, query).squeeze(2)  # [batch_size x seq_len x 1]
            ref = ref.permute(0, 2, 1)

        else:
            raise NotImplementedError

        if self.use_tanh:
            logits = self.C * F.tanh(logits)
        else:
            logits = logits
        return ref, logits


class GraphEmbedding(nn.Module):
    def __init__(self, input_size, embedding_size):
        super(GraphEmbedding, self).__init__()
        self.embedding_size = embedding_size
        self.embedding = torch.FloatTensor(input_size, embedding_size)
        if USE_CUDA:
            self.embedding = self.embedding.cuda()
        self.embedding = nn.Parameter(self.embedding)
        self.embedding.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))

    def forward(self, inputs):
        batch_size = inputs.size(0)
        seq_len = inputs.size(2)
        embedding = self.embedding.repeat(batch_size, 1, 1)
        embedded = []
        inputs = inputs.unsqueeze(1)
        for i in range(seq_len):
            a = torch.bmm(inputs[:, :, :, i].float(), embedding)
            embedded.append(a)
        embedded = torch.cat(embedded, 1)
        return embedded


class PointerNet(nn.Module):
    def __init__(self,
                 embedding_size,
                 hidden_size,
                 seq_len,
                 n_glimpses,
                 tanh_exploration,
                 use_tanh,
                 attention):
        super(PointerNet, self).__init__()

        self.embedding_size = embedding_size
        self.hidden_size = hidden_size
        self.n_glimpses = n_glimpses
        self.seq_len = seq_len

        self.embedding = GraphEmbedding(2, embedding_size)
        self.encoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
        self.decoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
        self.pointer = Attention(hidden_size, use_tanh=use_tanh, C=tanh_exploration, name=attention)
        self.glimpse = Attention(hidden_size, use_tanh=False, name=attention)

        self.decoder_start_input = nn.Parameter(torch.FloatTensor(embedding_size))
        self.decoder_start_input.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))

    def apply_mask_to_logits(self, logits, mask, idxs):
        batch_size = logits.size(0)
        clone_mask = mask.clone()

        if idxs is not None:
            clone_mask[[i for i in range(batch_size)], idxs.data] = 1
            logits[clone_mask] = -np.inf
        return logits, clone_mask

    def forward(self, inputs):
        """
        Args:
            inputs: [batch_size x 2 x sourceL]
        """
        batch_size = inputs.size(0)
        seq_len = inputs.size(2)
        assert seq_len == self.seq_len

        embedded = self.embedding(inputs)
        encoder_outputs, (hidden, context) = self.encoder(embedded)

        prev_probs = []
        prev_idxs = []
        mask = torch.zeros(batch_size, seq_len).byte()
        if USE_CUDA:
            mask = mask.cuda()

        idxs = None

        decoder_input = self.decoder_start_input.unsqueeze(0).repeat(batch_size, 1)

        for i in range(seq_len):

            _, (hidden, context) = self.decoder(decoder_input.unsqueeze(1), (hidden, context))

            query = hidden.squeeze(0)
            for i in range(self.n_glimpses):
                ref, logits = self.glimpse(query, encoder_outputs)
                logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
                query = torch.bmm(ref, F.softmax(logits).unsqueeze(2)).squeeze(2)

            _, logits = self.pointer(query, encoder_outputs)
            logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
            probs = F.softmax(logits)

            idxs = probs.multinomial().squeeze(1)
            for old_idxs in prev_idxs:
                if old_idxs.eq(idxs).data.any():
                    print(seq_len)
                    print(' RESAMPLE!')
                    idxs = probs.multinomial().squeeze(1)
                    break
            decoder_input = embedded[[i for i in range(batch_size)], idxs.data, :]

            prev_probs.append(probs)
            prev_idxs.append(idxs)

        return prev_probs, prev_idxs


class CombinatorialRL(nn.Module):
    def __init__(self,
                 embedding_size,
                 hidden_size,
                 seq_len,
                 n_glimpses,
                 tanh_exploration,
                 use_tanh,
                 reward,
                 attention):
        super(CombinatorialRL, self).__init__()
        self.reward = reward

        self.actor = PointerNet(
            embedding_size,
            hidden_size,
            seq_len,
            n_glimpses,
            tanh_exploration,
            use_tanh,
            attention)

        if USE_CUDA:
            self.actor = self.actor.cuda()

    def forward(self, inputs):
        """
        Args:
            inputs: [batch_size, input_size, seq_len]
        """
        batch_size = inputs.size(0)
        input_size = inputs.size(1)
        seq_len = inputs.size(2)

        probs, action_idxs = self.actor(inputs)

        actions = []
        inputs = inputs.transpose(1, 2)
        for action_id in action_idxs:
            actions.append(inputs[[x for x in range(batch_size)], action_id.data, :])

        action_probs = []
        for prob, action_id in zip(probs, action_idxs):
            action_probs.append(prob[[x for x in range(batch_size)], action_id.data])

        R = self.reward(actions)

        return R, action_probs, actions, action_idxs


class TrainModel:
    def __init__(self, model, train_dataset, val_dataset, batch_size=128, threshold=None, max_grad_norm=2.):
        self.model = model
        self.train_dataset = train_dataset
        self.val_dataset = val_dataset
        self.batch_size = batch_size
        self.threshold = threshold

        self.train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, num_workers=1)
        self.val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=True, num_workers=1)

        self.actor_optim = optim.Adam(model.actor.parameters(), lr=1e-4)
        self.max_grad_norm = max_grad_norm

        self.train_tour = []
        self.val_tour = []

        self.epochs = 0

    def train_and_validate(self, n_epochs):
        critic_exp_mvg_avg = torch.zeros(1)
        if USE_CUDA:
            critic_exp_mvg_avg = critic_exp_mvg_avg.cuda()

        for epoch in range(n_epochs):
            for batch_id, sample_batch in enumerate(self.train_loader):
                self.model.train()

                inputs = Variable(sample_batch)
                if USE_CUDA:
                    inputs = inputs.cuda()

                R, probs, actions, actions_idxs = self.model(inputs)

                if batch_id == 0:
                    critic_exp_mvg_avg = R.mean()
                else:
                    critic_exp_mvg_avg = (critic_exp_mvg_avg * beta) + ((1. - beta) * R.mean())

                advantage = R - critic_exp_mvg_avg

                logprobs = 0
                for prob in probs:
                    logprob = torch.log(prob)
                    logprobs += logprob
                logprobs[(logprobs < -1000).data] = 0.

                reinforce = advantage * logprobs
                actor_loss = reinforce.mean()

                self.actor_optim.zero_grad()
                actor_loss.backward()
                torch.nn.utils.clip_grad_norm(self.model.actor.parameters(),
                                              float(self.max_grad_norm), norm_type=2)

                self.actor_optim.step()

                # critic_exp_mvg_avg = critic_exp_mvg_avg.detach()

                self.train_tour.append(R.mean().data[0])

                if batch_id % 10 == 0:
                    self.plot(self.epochs)

                if batch_id % 100 == 0:

                    self.model.eval()
                    for val_batch in self.val_loader:
                        inputs = Variable(val_batch)
                        if USE_CUDA:
                            inputs = inputs.cuda()

                        R, probs, actions, actions_idxs = self.model(inputs)
                        self.val_tour.append(R.mean().data[0])

            if self.threshold and self.train_tour[-1] < self.threshold:
                print("EARLY STOPPAGE!")
                break

            self.epochs += 1

    def plot(self, epoch):
        clear_output(True)
        plt.figure(figsize=(20, 5))
        plt.subplot(131)
        plt.title('train tour length: epoch %s reward %s' % (
        epoch, self.train_tour[-1] if len(self.train_tour) else 'collecting'))
        plt.plot(self.train_tour)
        plt.grid()
        plt.subplot(132)
        plt.title(
            'val tour length: epoch %s reward %s' % (epoch, self.val_tour[-1] if len(self.val_tour) else 'collecting'))
        plt.plot(self.val_tour)
        plt.grid()
        # plt.show()
        plt.savefig('output.png')
        print('train tour length: epoch %s reward %s' % (
            epoch, self.train_tour[-1] if len(self.train_tour) else 'collecting'))
        print(
            'val tour length: epoch %s reward %s' % (epoch, self.val_tour[-1] if len(self.val_tour) else 'collecting'))
        print('\n')


if __name__ == '__main__':
    train_size = 1000000
    val_size = 10000
    seq_len = 20

    train_20_dataset = TSPDataset(seq_len, train_size)
    val_20_dataset = TSPDataset(seq_len, val_size)

    embedding_size = 128
    hidden_size = 128
    batch_size = 64
    n_glimpses = 1
    tanh_exploration = 10
    use_tanh = True

    beta = 0.9
    max_grad_norm = 2.

    tsp_20_model = CombinatorialRL(
        embedding_size,
        hidden_size,
        seq_len,
        n_glimpses,
        tanh_exploration,
        use_tanh,
        reward,
        attention="Dot")

    tsp_20_train = TrainModel(tsp_20_model,
                              train_20_dataset,
                              val_20_dataset,
                              threshold=3.99,
                              batch_size=batch_size)

    tsp_20_train.train_and_validate(5)

 

Basically, we should start from line 368 where the main function starts. In this code, we focus on travelling salesman problems of size 20 on a 2D plane. That means, each data point of  the training/validation dataset is a sequence of 20 2D points. Our goal is to search for a sequence of the given data points such that the loop trip for these data points has the shortest distance. Line 373 and 374 initialize the described datasets. In the following line (375 – 383), we set up model hyperparameters.

1. embedding_size is the dimension of transformed data from the original 2D data points. I think here the idea is to project 2D data into a higher dimension space such that richer information can be represented. It is possibly like devising a kernel in SVM [8] or like word embedding in NLP [9]. In line 173 (embedded = self.embedding(inputs) ), you can see that inputs to a pointer network must perform the embedding transformation first. (inputs size: batch_size x 2 x seq_len, embedded size: batch_size x seq_len x embedding_size)

2. n_glimpses is the number of glimpses to be performed in each decoder step (will explain more on it). However, since the author mentions in A.1 [1] that “We observed empirically that glimpsing more than once with the same parameters made the model less likely to learn and barely improved the results“, n_glimpses is simply set as 1. 

3. tanh_exploration and use_tanh correspond to Eqn.16 in A.2 in [1], which is claimed to “help with exploration and yield marginal performance gains“. 

We list the mapping between the paper parameters and the code parameters

paper parameter	note	code parameter
$latex x$	input sequence of $latex n$ cities	inputs
$latex \pi$	output sequence, permutation of $latex x$	actions
$latex n$	sequence length, the number of cities	seq_len
$latex d$	the size of hidden units	hidden_size
$latex B$	the size of Monte Carlo sampling for policy gradient	batch_size
$latex k$	the number of encoder vectors to reference in attention/glimpse model. It is usually the same as $latex n$

 

After the last line calling tsp_20_train.train_and_validate(5) , we come into the real meat and potato (line 284 to line 344):

a. at line 293~295, we get a batch of inputs (inputs size: batch_size x 2 x seq_len) 

b. at line 297 (R, probs, actions, actions_idxs = self.model(inputs) ), we pass inputs through a pointer network. We will talk about how the pointer network works. But for now, we just care about the workflow of TrainModel, which is essentially about training a policy gradient model called actor-critic.

Policy gradient is a family of models in which the objective function is to directly optimize rewards generated according to a parameterized policy. More details can be found in [3]. The paper gives the formulation under REINFORCE algorithm [10]:

 

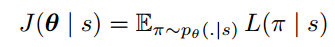
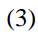
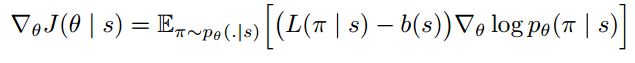
And the gradient of the policy (Eqn.4) can be approximated by the Monte Carlo method:

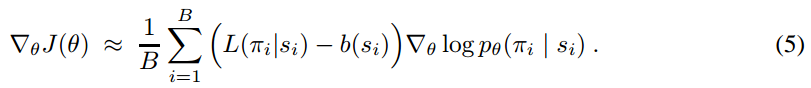
We can rewrite Eqn.5 to be more verbose, but more aligned to the codes:

$latex \nabla_\theta J(\theta) \approx \frac{1}{B}\sum\limits_{i=1}^B \nabla_\theta \sum\limits_{j=1}^n (L(\pi_i|s_i) – b(s_i)) \log p_\theta(\pi_i(j)|s_i) \;\; (5^*)&s=2$

Essentially, we expand $latex \log p_\theta(\pi_i | s_i)$ into $latex \sum\limits_{j=1}^n \log p_\theta(\pi_i(j) | s_i)$.

Since the learning framework like pytorch will compute the gradient automatically for us, we only need to compute $latex \frac{1}{B}\sum\limits_{i=1}^B \sum\limits_{j=1}^n (L(\pi_i|s_i) – b(s_i)) \log p_\theta(\pi_i(j)|s_i)&s=2$ using R and probs (line 306-320).

parameter	note	size
R	rewards, $latex L(\pi_i|s_i)$	batch_size
actions	output data points	seq_len x batch_size x 2
action_idxs	output the order of input data points	seq_len x batch_size
probs	the probability of each $latex p_\theta(\pi_i(j)|s_i)$	seq_len x batch_size

 

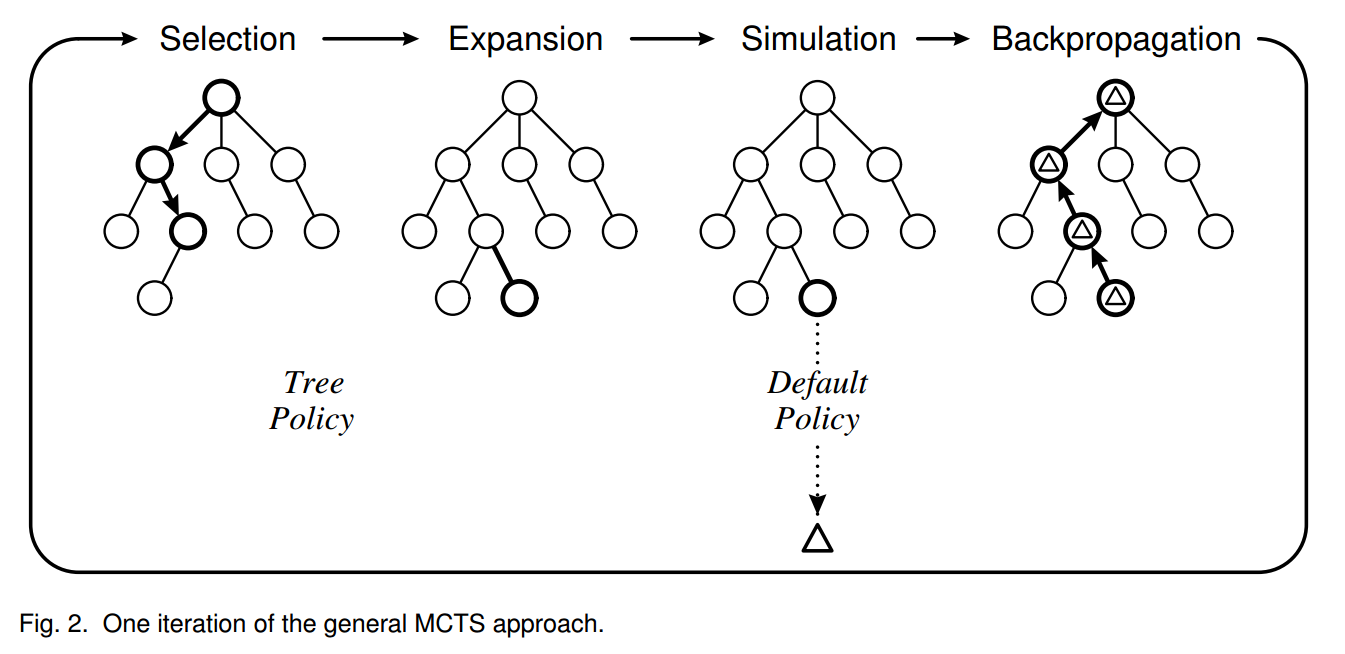
Now, let’s transition to understand how the pointer network works (line 164-212). In line 174, self.encoder is a LSTM initiated at line 147. Since it is initialized with batch_first=True, embedded‘s size is batch_size x seq_len x embedding_size, with the batch_size as the first dimension. The output, encoder_outputs, also has the same size. (See [12] for pytorch I/O LSTM format.)

We are going to use the plot from the paper to further illustrate how the pointer network works. First, let’s get clear about where encoder_inputs (embedded) and encoder_outputs are.

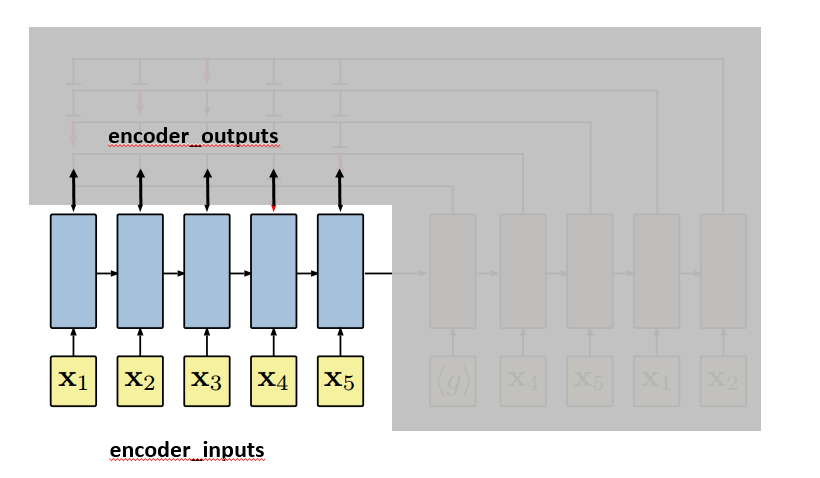
Each blue block is the LSTM unit which takes input repeatedly. Since in line 174, self.encoder is fed without hidden and context parameter, hidden and context for the first input are treated as zero vectors [12]. LSTM will output, besides encoder_outputs, hidden and context layers:

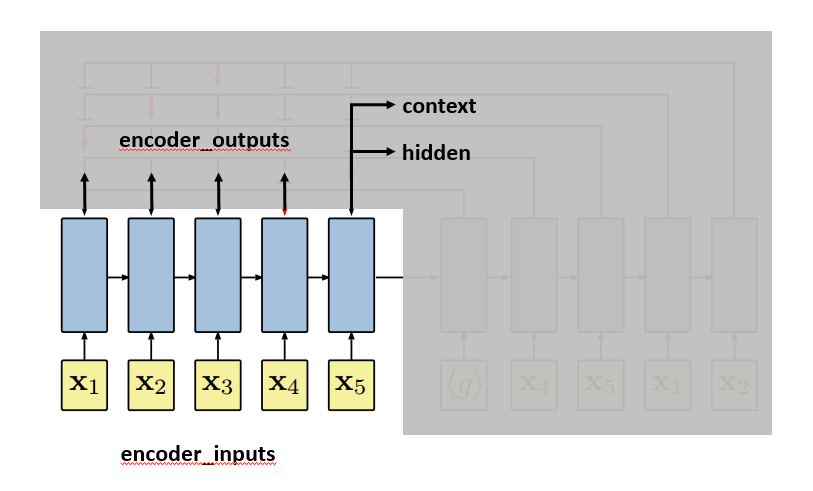
After the last input passes the encoder, the decoder will start. The first input to the decoder, denoted by <g>, is a vector of the same embedding size as the inputs. And it is treated as a trainable parameter.  The first hidden and context vectors to the decoder are the last hidden and context vectors of the encoder. The decoder will output context and hidden vectors at each step.

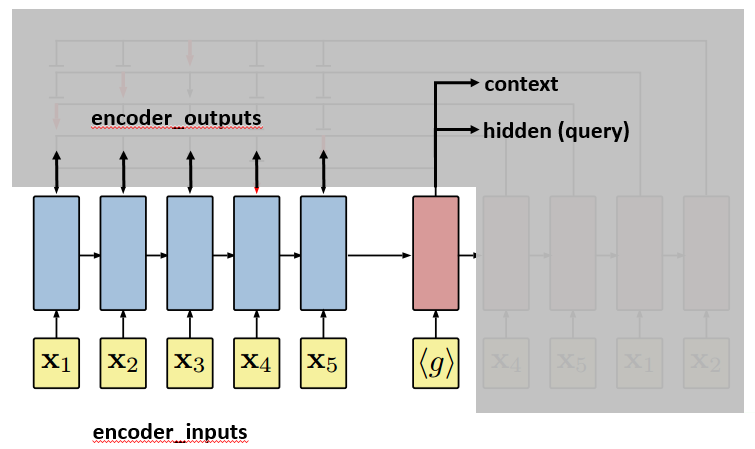
The hidden vector of the decoder, together with encoder_outputs, will be used by an attention model to select an output (city) at each step. Before hidden is sent to the attention model, the paper suggests to process it by a technique called “glimpse”. The basic idea is to not use hidden directly in the attention model, but use query=glimpse(hidden, encoder_outputs) $latex \in \mathbb{R}^d$. Te author says that “The glimpse function G essentially computes a linear combination of the reference vectors weighted by the attention probabilities“. Note the two things:

1. the attention model to select output cities and the glimpse model are both attention models. The difference between the two is that the glimpse model outputs a vector with $latex d$ dimension to replace the hidden vector of the decoder while the attention model to select output cities outputs a vector with $latex k$ dimension, which refers to the probability distribution of selecting each of the $latex k$ reference vectors.
2. Due to the nature of the problem, there cannot be duplicate cities in the output sequence. Therefore we have to manually disable those already outputted cities using the function apply_mask_to_logits.

Finally, it comes to the attention model. The attention model will take as input the query vector and encoder_outputs. As we said, the attention model will output a probability distribution of length $latex k$, the number of reference vectors. $latex k$ is usually equal to $latex n$ because we reference all the input cities.

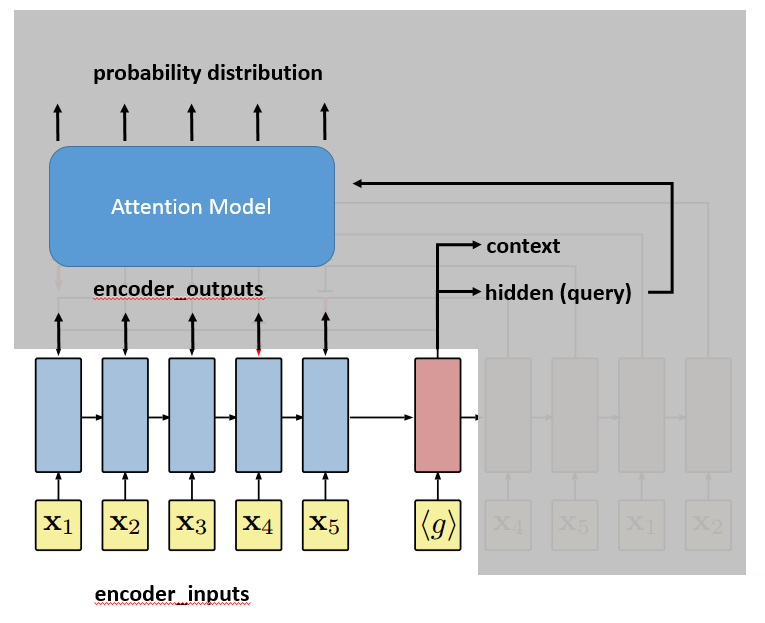
Line 200~206 finally selects the output city according to the probability distribution. 

In line 207, we prepare the next input to the decoder, which is the embedding of the city just outputted.

The following table lists the sizes of all appeared parameters.

parameter	size
embedded	batch_size x seq_len x embedding_size
encoder_outputs	batch_size x seq_len x hidden_size
hidden	1 x batch_size x hidden_size
context	1 x batch_size x hidden_size
query	batch_size x hidden_size
logits	batch_size x seq_len

 

Let’s pretty much about it.

 

Reference:

[1] Neural Combinatorial Optimization With Reinforcement Learning: https://arxiv.org/abs/1611.09940

[2] Pointer Networks: https://arxiv.org/abs/1506.03134

[3] https://czxttkl.com/?p=2812

[4] https://czxttkl.com/?p=1819

[5] https://czxttkl.com/?p=1047

[6] https://czxttkl.com/?p=3109

[7] https://github.com/higgsfield/np-hard-deep-reinforcement-learning

[8] https://czxttkl.com/?p=3114

[9] https://czxttkl.com/?p=2530

[10] Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning: http://www-anw.cs.umass.edu/~barto/courses/cs687/williams92simple.pdf

[12] http://pytorch.org/docs/master/nn.html#torch.nn.LSTM

This post reviews the key knowledgement about support vector machine (SVM). The post is pretty much based on a series of the lectures [1].

Suppose we have data , where each point is a -dimensional data point associated with label .

The very initial SVM is to come up with a plane such that data points can be perfectly linearly divided according to their labels. For a linearly separable dataset, there can exist infinite such plane. However, the “best” one, intuitively, should have the largest margins from all the closest points to it. Here, “margin” means the distance from a point to a plane. As an example below, the best separating plane is supposed to be the rightmost one.

For a data point , the way to calculate its margin (i.e., its distance to the plane , is to pick a point on the plane and then project onto :

Since any point on the plane satisfies that , we can simplify the distance formula:

(From an intuitive perspective, the vector is perpendicular to the plane . Therefore the distance from to the hyperplane is to find the projection of onto the direction .)

This is the margin for any data point . However, remember that the ultimate goal is to maximize the margin of the data point, the data point which is the closest to the separating plane. One can write the objective function like this:

A problem arises here. Even for the same plane, there can be infinite sets of corresponding to it, all with different scales. For example, the plane with is the same plane as the plane with . Therefore, we need to pre-define a scale.

We propose a normalization standard: normalize and such that the closest data point to the plane, , has: . Therefore, the distance from the closest data point to the plane becomes . After this, the objective function becomes easier:

Note that for any data point , . The constraints can be re-written as . Moreover, instead of maximizing , we can minimize equivalently. Therefore, the objective function now becomes:

We are sure that for all the constraints, there must be at least one constraint where the equality holds (i.e., for some data point , ). That is the data point which is the closest to the plane. If all the constraints only have the inequality hold (i.e., ), would not be minimized: we can always scale down a little bit such that decreases until some constraint hits the equality.

The objective function is a constrained optimization problem with affine inequality constraints. An overview of using Lagrange/KKT to do optimization can be found in my previous post [2]. Basically, the way to optimize this objective function is to use Lagrange multiplier and KKT condition.

From [2], we know that KKT condition is usually a necessary condition in a constrained optimization problem. However, when the optimization problem is convex (in our case ) and Slater’s condition holds (in our case, we only have linear constraints ), KKT condition becomes a sufficient and necessary condition for finding the optimal solution . will be the saddle point of the Lagrange multiplier augmented loss function . Regarding why we can apply Lagrange multiplier + KKT condition to optimize the objective function, please refer to other materials also, since this is the part I am less confident about: (Section 3.2 in [4], answer in [5], slides in [6], Section 5.2.3 in [7]).

The optimization process is as follows. We first write the Lagranger formulation and take the derivatives of the Lagranger formulation w.r.t. and . Setting the derivatives to 0 we can find the relationship between (the Lagranger multipler), , and (data).

We can eventually formulate the problem as a quadratic programming problem (w.r.t. ) and then hand it to a quadratic programming package to solve it. We are expected to receive the vector as results, which then we will use to obtain .

Then, the parameter can be obtained by picking a support vector and solve by .

Until this point, a new problem arises: we have been only dealing with perfectly linearly separable problems. How can we apply SVM in non-linear problems?

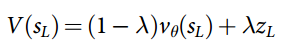
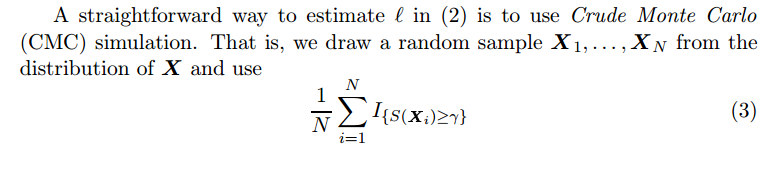
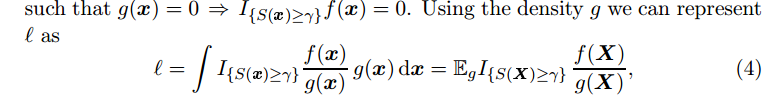
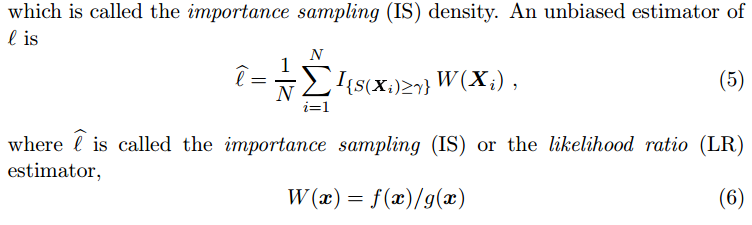
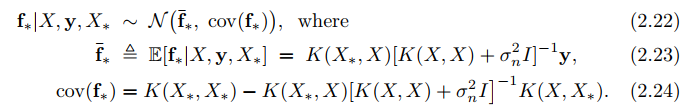
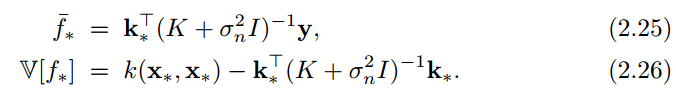
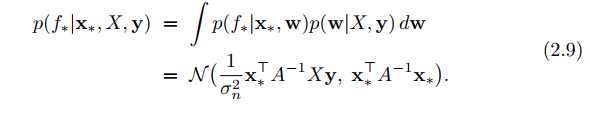
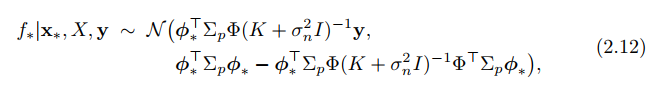
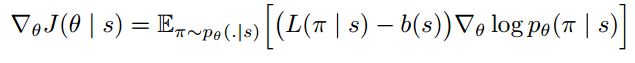
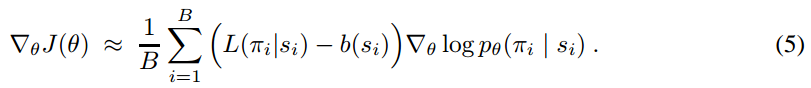
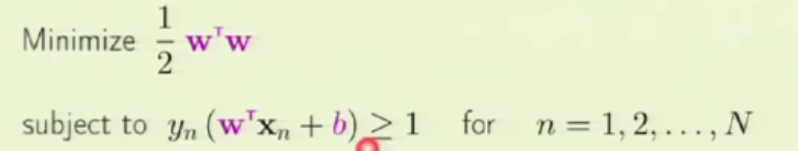
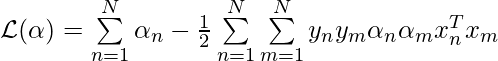The first solution is kernel trick. Our objective function sending to quadratic programming is , which only requires we know the inner product between any and . Suppose in the original form of raw data, are low-dimensional data points that are not linearly separable. However, if they are mapped to a higher dimension as , they can be separable. On that high dimension space, we can apply the linear separable SVM version on the data points to find a hyperplance and support vectors. That only requires we know the inner product of and .

We don’t even need to know the exact formula of the mapping function from : even a black-box mapping function is ok, as long as we can calculate the inner product of any and corresponding to and .  This “inner product” value function is called kernel:

Kernel functions can have many forms. For example, polynomial kernel: and Radial Basis Function kernel: . There is a math property called “Mercer’s condition” that an be used to verify whether a function is a valid kernel function. But this is out of the scope of this post.

After we use kernel, the optimization of SVM stays the same except that the coefficient matrix of quadratic programming now becomes:

And to finally obtain and , we need to utilize kernel function too:

The second solution to deal with non-linearly separable problems is to use soft-margin. The intuition is to allow some violation of the margin constraint for some data points.

To compare the two solutions, we find that the kernel solution is often used when data are highly non-linearly separable. The soft-margin SVM is often used when data is just slightly non-linearly separable (most data are still linearly separable).

About practical issues of applying SVM, please refer to [3].

Reference

[1] lectures from Caltech online ML course

https://www.youtube.com/watch?v=eHsErlPJWUU

and

https://www.youtube.com/watch?v=XUj5JbQihlU

[2] https://czxttkl.com/?p=1449

[3] https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf

[4] http://www.cmap.polytechnique.fr/~mallat/papiers/svmtutorial.pdf

[5] https://stats.stackexchange.com/questions/239912/lagrange-multipler-kkt-condition

[6] https://www.cs.cmu.edu/~epxing/Class/10701-08s/recitation/svm.pdf

[7] convex optimization textbook: https://www.dropbox.com/s/fk992yb6qja3xhv/convex%20optimization.pdf?dl=0

Some chinese references:

[a] http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html

[b] http://blog.csdn.net/v_july_v/article/details/7624837

Travelling salesman problem (TSP) goes as follows [1]:

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?

This problem statement is actually a TSP-OPT problem., where”OPT” stands for optimization. This is not a decision problem since the answer to it is not simply “yes”/”no”.  The decision version of TSP is:

Given a list of cities and the distances between each pair of cities, does there exist a  route that visits each city with the total distance less than or equal to k?

According to Section “How to prove NP-completeness in practice” in [2] and the top answer in [3], in order to prove a decision problem is NP-complete, we need to prove (1) it is in NP (2) another known NP-complete problem can be polynomially reducible to your problem

Alternatives to prove (2) are:

a. argue that if you can solve a known NP-complete problem in polynomial time, then you can solve your problem in polynomial time

b. construct an algorithm to solve your problem that only calls the oracle of a known NP-complete problem polynomial times and does extra works outside the oracle in polynomial time such that the algorithm returns yes iff the oracle returns yes. 

c. similar to b, construct an algorithm to solve your problem that only calls the oracle of a known NP-complete problem polynomial times and does extra works outside the oracle in polynomial time such that (i) the algorithm returns yes if the oracle returns yes and (ii) the algorithm returns no if the oracle returns no.

NP means the class of all decision problems where “yes” answers can be verified efficiently[7, 10th slide]. It is a property regarding only decision problems. Therefore, we can show that TSP-DEC is NP-complete. However, we can never say TSP-OPT is NP-complete [10]. 

The proof of TSP-DEC is NP-complete can be found: [6], [8], [9]. The basic idea is to reduce from Hamiltonian-cycle problem which is known to be NP-complete.

Similarly, there are many tutorials on proving independent-set problem is a NP-complete problem [4, 5].  

Although we can’t say TSP-OPT is NP-complete because it is not even a decision problem, we can say TSP-OPT is a NP-hard problem because TSP-OPT is self reducible from TSP-DEC. From a reply from [10]:

This means, TSP-OPT can be solved just in polynomial scale of the time solving TSP-DEC.

More words about self-reducible. A good tutorial of self-reducible can be found in [11, 12, 13]. It seems like (I haven’t verified) that “Every NP-Complete problem/language L is self-reducible” (from Theorem 24.3.4 in [12]). That means, all NP-complete optimization problems can be polynomially reducible to their decision problems.

 

Reference

[1] https://en.wikipedia.org/wiki/Travelling_salesman_problem

[2] http://www.ics.uci.edu/~eppstein/161/960312.html

[3] https://stackoverflow.com/questions/4294270/how-to-prove-that-a-problem-is-np-complete

[4] http://www.cs.cornell.edu/courses/cs482/2004su/handouts/NPComplete.pdf

[5] https://perso.esiee.fr/~mustafan/TechnicalWritings/Complexityslides/lec6.pdf

[6] https://www.quora.com/Why-is-the-traveling-salesman-problem-NP-complete

[7] https://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/19/Small19.pdf

[8] https://www.researchgate.net/file.PostFileLoader.html?id=58a153df40485494272392f9&assetKey=AS%3A461190431285249%401486967775832

[9] https://math.stackexchange.com/questions/1077436/the-traveling-salesman-problem-is-np-complete-reduction

[10] http://www.nomachetejuggling.com/2012/09/14/traveling-salesman-the-most-misunderstood-problem/

[11] http://www.cs.toronto.edu/~fpitt/20109/CSC363/lectures/LN11.txt

[12] https://courses.engr.illinois.edu/cs473/fa2011/lec/24_notes.pdf

[13] https://cseweb.ucsd.edu/~mihir/cse200/decision-search.pdf