In this post, I am summarizing all I know for optimization. It is a hard, primary problem once you define your model with some kind of objective function integrating a bunch of parameters and you start to wonder how you could learn the values of those parameters to minimize (or maximize) the objective function.
Unconstrained Optimization
You wish to learn parameters to minimize the objective function and those parameters don’t have any constraints. If this is a convex problem, then there must be a global minimum and you can find it by finding all points whose first-order derivatives are zero. If the objective function is not convex, don’t panic. Gradient Descent (with lots of its variants such as momentum gradient descent, stochastic gradient descent, AdaGra) definitely help you to reach local minimum. People find that when the number of variables is large you will reach a not too bad local minimum. (missing reference here). Another family of approach is called quasi-Newton method which is my favorite. They have comparably fast speed as Newton Method does but its computation is way more economic. I implemented one unconstrained LBFGS algorithm in Python and some of its details are revealed here: https://czxttkl.com/?p=1257
Constrained Optimization
When it comes to constrained optimization, there exist tons of approaches which can be applied in different conditions. Here is a summary of techniques you can equip: (from https://ipvs.informatik.uni-stuttgart.de/mlr/marc/teaching/13-Optimization/03-constrainedOpt.pdf):
First of all, let’s get familiar with the foundations of constrained optimization.
Suppose we are faced a constrained optimization problem:
![]()
s.t. ![]() and
and ![]()
At a feasible point ![]() , the inequality constraint
, the inequality constraint ![]() is said to be active if
is said to be active if ![]() and inactive if the strict inequality
and inactive if the strict inequality ![]() is satisfied.
is satisfied.
The active set ![]() at any feasible
at any feasible ![]() consists of the equality constraint indices from
consists of the equality constraint indices from ![]() together with the indices of the inequality constraints
together with the indices of the inequality constraints ![]() for which
for which ![]() , i.e.,
, i.e., ![]()
LICQ: Given the point ![]() and the active set
and the active set ![]() , we say that the linear independence constraint qualification (LICQ) holds if the set of the active constraint gradient
, we say that the linear independence constraint qualification (LICQ) holds if the set of the active constraint gradient ![]() is linearly independent.
is linearly independent.
KTT (Karush-Kuhn-Tucker) conditions
KTT conditions are necessary conditions for a optimum solution in nonlinear programming. (Some of the constraints or the objective function is non-linear.) In other words, if a solution ![]() is a local minimum of a function
is a local minimum of a function ![]() which we aims to minimize under certain equality constraints
which we aims to minimize under certain equality constraints ![]() and inequality constraints
and inequality constraints ![]() , then
, then ![]() ,
, ![]() ,
, ![]() and
and ![]() must satisfy KTT conditions. The reverse, i.e., if a solution
must satisfy KTT conditions. The reverse, i.e., if a solution ![]() satisfies KTT conditions then it is a local minimum, is not always true.
satisfies KTT conditions then it is a local minimum, is not always true.
More formally to state KTT conditions:
Assume ![]() is a local solution which achieves local minimum of
is a local solution which achieves local minimum of ![]() . If
. If ![]() ,
, ![]() and
and ![]() are continuously differentiable, and LICQ holds at
are continuously differentiable, and LICQ holds at ![]() , then there is a Lagrange multiplier vector
, then there is a Lagrange multiplier vector ![]() , with components
, with components ![]() , such that following conditions are satisfied at
, such that following conditions are satisfied at ![]() :
:
- Define:
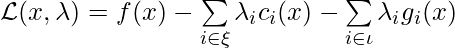
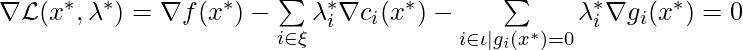
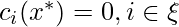
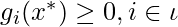
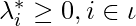
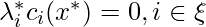
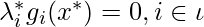
In ![]() , we ignore to subtract
, we ignore to subtract 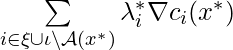 because KKT conditions indicate that
because KKT conditions indicate that![]() for
for ![]() , i.e., for those inactive inequality constraints
, i.e., for those inactive inequality constraints ![]() .
.
Note that, we require LICQ holds at ![]() so that
so that ![]() is unique. LICQ is called constraint qualification. There are other constraint qualifications that must hold to guarantee KKT conditions hold if
is unique. LICQ is called constraint qualification. There are other constraint qualifications that must hold to guarantee KKT conditions hold if ![]() is a local minimum. (See https://www.math.washington.edu/~burke/crs/516/notes/cq_lec.pdf) For example, if
is a local minimum. (See https://www.math.washington.edu/~burke/crs/516/notes/cq_lec.pdf) For example, if ![]() is a local minimum and Abadie constraint qualification (ACQ) holds at
is a local minimum and Abadie constraint qualification (ACQ) holds at ![]() , then KTT conditions still hold. Here ACQ is a weaker constraint qualification than LICQ because LICQ => ACQ.
, then KTT conditions still hold. Here ACQ is a weaker constraint qualification than LICQ because LICQ => ACQ.
Here is my rough understanding of KKT conditions: We want to let ![]() subject to the same constraints.
subject to the same constraints. ![]() consists of
consists of ![]() and a bunch of
and a bunch of ![]() and
and ![]() . To make sure
. To make sure ![]() and
and ![]() have the same local solution
have the same local solution ![]() , you must do the following checks:
, you must do the following checks:
- For a local minimum
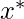 of
of 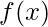 , if
, if 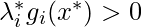 , then
, then 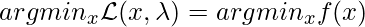 is not guaranteed unless
is not guaranteed unless 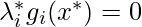 . Put it in other words, if you want
. Put it in other words, if you want 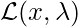 to have the same optimum as
to have the same optimum as 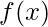 , then
, then 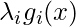 , the term added to
, the term added to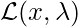 besides
besides 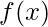 , should not influence
, should not influence 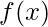 and
and 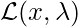 to reach their local minimum at
to reach their local minimum at 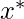 at the same time.
at the same time. - For equality constraints and active inequality constraints,
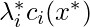 and
and 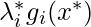 are zeros which can be safely added to
are zeros which can be safely added to 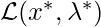 without affecting
without affecting 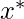 being the local optimum for both
being the local optimum for both 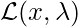 and
and 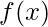 .
.
Next, you should note that for the local minimum ![]() ,
,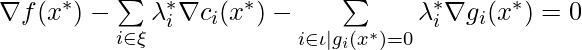 . This means, at
. This means, at ![]() , the force to minimize
, the force to minimize ![]() is pulled by the force to ensure
is pulled by the force to ensure ![]() to stay in feasible areas. This can be illustrated in the following example:
to stay in feasible areas. This can be illustrated in the following example:
As you can see, at ![]() , the force to minimize
, the force to minimize ![]() is the direction
is the direction ![]() (marked as purple arrow) . The force to pull
(marked as purple arrow) . The force to pull ![]() to stay the feasible region (the square in the middle) is
to stay the feasible region (the square in the middle) is ![]() and
and ![]() (marked as red arrows).
(marked as red arrows). ![]() makes sure
makes sure ![]() ,
, ![]() and
and ![]() are linearly dependent at this point so that
are linearly dependent at this point so that ![]() can’t be dragged any further by any force.
can’t be dragged any further by any force.

Although knowing a feasible point ![]() and a
and a ![]() satisfying KTT conditions is generally not sufficient to conclude
satisfying KTT conditions is generally not sufficient to conclude ![]() is the solution for the constrained optimization problem, under certain conditions
is the solution for the constrained optimization problem, under certain conditions ![]() indeed is the solution. For example, if you know additional information like Second Order Sufficient Conditions, then KTT conditions become sufficient to say
indeed is the solution. For example, if you know additional information like Second Order Sufficient Conditions, then KTT conditions become sufficient to say ![]() is a local solution. For another example, if Slater’s condition holds for the constrained problem, then
is a local solution. For another example, if Slater’s condition holds for the constrained problem, then ![]() . (Ref: http://math.stackexchange.com/questions/379543/kkt-and-slaters-condition, https://www.cs.cmu.edu/~ggordon/10725-F12/slides/16-kkt.pdf p11). In the famous SVM model, the objective function and its constraints also satisfies Slater’s condition such that KTT conditions are sufficient and necessary. See https://czxttkl.com/?p=3114 for how we do optimization for SVM using KTT.
. (Ref: http://math.stackexchange.com/questions/379543/kkt-and-slaters-condition, https://www.cs.cmu.edu/~ggordon/10725-F12/slides/16-kkt.pdf p11). In the famous SVM model, the objective function and its constraints also satisfies Slater’s condition such that KTT conditions are sufficient and necessary. See https://czxttkl.com/?p=3114 for how we do optimization for SVM using KTT.
Actually, Slater’s condition is originally used to prove that the strong duality holds for the constrained problem. Let’s illustrate it by introducing Duality Theory.
Duality Theory
An optimization problem can usually be constructed as a primal problem, for which there exists a corresponding dual problem. The dual problem sometimes has magics such that the computation of the dual problem is easier, or the solution of the dual problem can hint bounds of the primal problem.
Let’s say we face the same optimization problem as follows.
![]()
s.t. ![]() and
and ![]()
This problem can be converted into a primal problem incorporating all the constraints ![]() and
and ![]() :
:
![]() subject to
subject to ![]()
Why does the primal problem look like this? This is because the minimum of ![]() is the same as the minimum of the original constrained optimization problem. For those
is the same as the minimum of the original constrained optimization problem. For those ![]() s.t.
s.t. ![]() ,
, ![]() therefore any
therefore any ![]() violating the constraints is definitely not the solution to the primal problem. For those
violating the constraints is definitely not the solution to the primal problem. For those ![]() satisfying the constraints,
satisfying the constraints, ![]() . Therefore, it is equivalent to
. Therefore, it is equivalent to ![]() as to do the original constrained problem.
as to do the original constrained problem.
Now we construct the dual problem of the primal problem. The dual problem is:
![]() subject to
subject to ![]() . (Here
. (Here ![]() is infimum function denoting the lower bound of
is infimum function denoting the lower bound of ![]() . For example,
. For example, ![]() . We don’t use
. We don’t use ![]() to denote the lower bound of
to denote the lower bound of ![]() because
because ![]() can be infinitely close to but never reach the lower bound for any
can be infinitely close to but never reach the lower bound for any ![]() .)
.)
Now we have Weak Duality which goes like this:
![]() for any
for any ![]() and any feasible
and any feasible ![]()
This suggests that the optimum of the dual problem has some non-negative duality gap smaller than the optimum of the primal problem. If we can close the duality gap between the dual and the primal, we can solve the primal problem by solving the dual problem which sometimes is much easier. The duality gap is zero when Strong Duality holds for the optimization problem.
Ref: http://jackvalmadre.tumblr.com/post/15798388985
Here for the duality theory for linear programming specifically: https://www.math.washington.edu/~burke/crs/407/notes/section4.pdf
Lagrange Multiplier
Lagrange Multiplier is used for finding minimum/maximum of a function under equality constraints. Lagrange Multiplier utilizes an important fact that when a function achieves a minimum/maximum under certain equality constraints, the gradient of the function and the gradients of the constraints have the same direction. What Lagrange Multiplier essentially does is to add constraints, each multiplied by a Lagrange Multiplier, to the objective function to form an “auxiliary objective function”. By taking the derivative of the auxiliary objective function and set it to zero, we can find all stationary points of the auxiliary objective function. Among those stationary points, there must be at least one that achieves the minimum/maximum. A good tutorial of Lagrange Multiplier can be found here: http://www.slimy.com/~steuard/teaching/tutorials/Lagrange.html
Lagrange Multiplier method can be modified to solve constrained problems with inequality constraints. The multiplier and optimal solution can be found by using KKT conditions: http://www.csc.kth.se/utbildning/kth/kurser/DD3364/Lectures/KKT.pdf. One example of using Lagrange Multiplier to solve problems with inequality constraints can be found here: http://users.wpi.edu/~pwdavis/Courses/MA1024B10/1024_Lagrange_multipliers.pdf.
A family of constrained problem solvers converts constrained problems into unconstrained problems. In the family of such solvers, one kind of algorithms are called inexact method: the solution to the transformed unconstrained problem is close but not exactly the same to that to the original constrained problem. The other kind of algorithm is called exact method in which the solution does not change after the transformation. In the following introduced algorithms, Quadratic Penalty Method belongs to inexact method. ![]() Penalty Method and Augmented Lagrangian Method belong to exact method.
Penalty Method and Augmented Lagrangian Method belong to exact method.
Quadratic Penalty Method

![]() Penalty Method
Penalty Method
When only equality constraints are present, ![]() is smooth. But when inequality constraints are also present,
is smooth. But when inequality constraints are also present, ![]() is not smooth any more. Moreover,
is not smooth any more. Moreover, ![]() sometimes goes to be very large in iterations, likely to cause the Hessian matrix of
sometimes goes to be very large in iterations, likely to cause the Hessian matrix of ![]() ,
, ![]() , become ill-conditioned.
, become ill-conditioned.
![]() Penalty Method
Penalty Method
![]() Penalty Method is exact but the non-smoothness of
Penalty Method is exact but the non-smoothness of ![]() makes it difficult to find minimizer of it. Refer to the textbook to some hack ways to solve it.
makes it difficult to find minimizer of it. Refer to the textbook to some hack ways to solve it.
Augmented Lagrangian Method
It reduces the possibility of ill-conditioning of Quadratic Penalty Method and preserves the smoothness as opposed to ![]() Penalty Method.
Penalty Method.
https://en.wikipedia.org/wiki/Augmented_Lagrangian_method
Stochastic Gradient Descent
Stochastic Gradient Descent has been popular among large-scale machine learning. So far the most canonical text about stochastic gradient descent I’ve found is: Bottou, L. (2012). Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade (pp. 421-436). Springer Berlin Heidelberg.
The core idea is that “use stochastic gradient descent when training time is the bottleneck“. What does this mean? Roughly understanding, gradient descent should result in higher training accuracy than its stochastic counterpart because the former uses the full dataset to calculate a less noisy weight update. However in an iteration, gradient descent will take a long time to traverse all samples to calculate weight update. During that, the weight update of stochastic gradient descent has happened many times and the objective function it optimizes has been improved many times! Therefore, the paper points out that “SGD needs less time than the other algorithms to reach a predefined expected risk”. Please understand Table 2 in the paper carefully.
Projected Gradient Descent
This post highly summarizes the difference between ordinary gradient descent and projected gradient descent: http://math.stackexchange.com/questions/571068/what-is-the-difference-between-projected-gradient-descent-and-ordinary-gradient
This paper showcases how to use projected gradient descent for non-negative matrix factorization:
Lin, C. J. (2007). Projected gradient methods for nonnegative matrix factorization. Neural computation, 19(10), 2756-2779.
This paper also points out that if all the constraints are just non-negativity constraint, then we can set parameters ![]() , then we can just optimize the objective w.r.t
, then we can just optimize the objective w.r.t ![]() , where
, where ![]() .
.
However, I have not seen projected stochastic gradient descent been applied on any problem. I will keep searching why it is rarely used. My guess is that stochastic-based updates are already very noisy and unstable. The projection performed after each stochastic update will make parameter updates even more unstable such that the optimization cannot find the correct path towards the optimal parameterization.
Quadratic Programming
Quadratic Programming is an optimization problem with a quadratic objective function and linear constraints. If constraints only consist of equalities, it looks like the following:
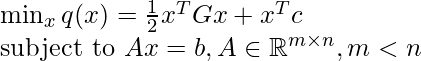
Now we introduce an iterative way to solve the quadratic programming with equality constraints, which is covered in Chapter 16.3 of Numerical Optimization by Nocedal & Wright.
First, the optimal solution ![]() can be represented as
can be represented as ![]() , where
, where ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . Note that in
. Note that in ![]() ,
, ![]() ,
, ![]() and
and ![]() are some constants determined by elimination algorithms (introduced soon).
are some constants determined by elimination algorithms (introduced soon). ![]() is the free variables that
is the free variables that ![]() . Why can
. Why can ![]() be represented by
be represented by ![]() ? This is because
? This is because ![]() has rank
has rank ![]() (
(![]() ) therefore we can use
) therefore we can use ![]() variables in
variables in ![]() to represent
to represent ![]() variables in
variables in ![]() . Since
. Since ![]() ,
, ![]() indicates that
indicates that ![]() . Therefore,
. Therefore, ![]() is a solution satisfying
is a solution satisfying ![]() . Therefore,
. Therefore, ![]() can be seen as a sum of a particular solution to the constraint
can be seen as a sum of a particular solution to the constraint ![]() (the first term) plus a transformation
(the first term) plus a transformation ![]() applied on
applied on ![]() . Since
. Since ![]() holds, any choice of
holds, any choice of ![]() will still satisfy the constraint
will still satisfy the constraint ![]() . The only difference of choices of
. The only difference of choices of ![]() remains to be whether
remains to be whether ![]() minimizes the objective function.
minimizes the objective function.
To determine ![]() ,
, ![]() and
and ![]() , we use methods called simple elimination or general elimination:
, we use methods called simple elimination or general elimination:
1. simple elimination says that: find a permutation matrix ![]() such that
such that ![]() . Here the columns of
. Here the columns of ![]() are a subset of columns of
are a subset of columns of ![]() that are linearly independent.
that are linearly independent. ![]() . Now that if we set:
. Now that if we set: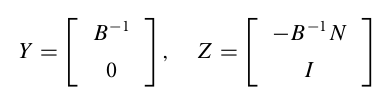
, ![]() can be represented as
can be represented as ![]() .
.
2. general elimination uses QR-factorization on ![]() (
(![]() is a permutation matrix to obtain
is a permutation matrix to obtain ![]() ,
, ![]() and
and ![]() :
:
(I am unclear of when to use simple elimination or general elimination as the book compares the two algorithms vaguely to me. )
Now let’s go back solving the quadratic programming problem once obtaining ![]() . Plugging it to
. Plugging it to ![]() with all constants removed, we obtain
with all constants removed, we obtain ![]() . The textbook gives an iterative method to find desired
. The textbook gives an iterative method to find desired ![]() using Conjugate Gradient method, with the assumption that
using Conjugate Gradient method, with the assumption that ![]() is positive definite:
is positive definite:
![]() regularization
regularization
Please note that ![]() regularization refers to the problem of the form:
regularization refers to the problem of the form: ![]() . Such forms of problems often have solutions
. Such forms of problems often have solutions ![]() with great sparsity. That is why
with great sparsity. That is why ![]() regularization is often used to achieve feature selection. This kind of problem is different to another kind of problem (also introduced in this post): use
regularization is often used to achieve feature selection. This kind of problem is different to another kind of problem (also introduced in this post): use ![]() as nonsmooth exact penalty function to solve constrained problems.
as nonsmooth exact penalty function to solve constrained problems.
This paper gives a full overview of methods to solve ![]() regularization problems. I am here giving a simple approach:
regularization problems. I am here giving a simple approach:
When given a ![]() regularization problem
regularization problem ![]() , we can write an equivalent constrained optimization problem:
, we can write an equivalent constrained optimization problem: 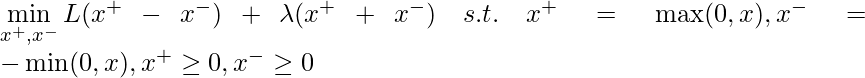
To explain why we can write such equivalent constrained optimization problem, let’s first check that ![]() and
and ![]() . Therefore
. Therefore ![]() and
and ![]() . Depending on the strength of
. Depending on the strength of ![]() ,
, ![]() and
and ![]() will be constrained to not fluctuate too radically, resulting the constrained
will be constrained to not fluctuate too radically, resulting the constrained ![]() norm of original
norm of original ![]() . Eventually, the
. Eventually, the ![]() regularization problem becomes a box constraint optimization problem (albeit the box is single side bounded, because you only require
regularization problem becomes a box constraint optimization problem (albeit the box is single side bounded, because you only require ![]() and
and ![]() to be non-negative.)
to be non-negative.)
There is an online implementation of such method using L-BFGS-B (box constraint of L-BFGS): https://gist.github.com/vene/fab06038a00309569cdd
Coordinate Descent
https://www.cs.cmu.edu/~ggordon/10725-F12/slides/25-coord-desc.pdf
Some Topics to Explore
Non convex global optimization: http://mathoverflow.net/questions/32533/is-all-non-convex-optimization-heuristic