Travelling salesman problem (TSP) goes as follows [1]:
Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?
This problem statement is actually a TSP-OPT problem., where”OPT” stands for optimization. This is not a decision problem since the answer to it is not simply “yes”/”no”. The decision version of TSP is:
Given a list of cities and the distances between each pair of cities, does there exist a route that visits each city with the total distance less than or equal to k?
According to Section “How to prove NP-completeness in practice” in [2] and the top answer in [3], in order to prove a decision problem is NP-complete, we need to prove (1) it is in NP (2) another known NP-complete problem can be polynomially reducible to your problem
Alternatives to prove (2) are:
a. argue that if you can solve a known NP-complete problem in polynomial time, then you can solve your problem in polynomial time
b. construct an algorithm to solve your problem that only calls the oracle of a known NP-complete problem polynomial times and does extra works outside the oracle in polynomial time such that the algorithm returns yes iff the oracle returns yes.
c. similar to b, construct an algorithm to solve your problem that only calls the oracle of a known NP-complete problem polynomial times and does extra works outside the oracle in polynomial time such that (i) the algorithm returns yes if the oracle returns yes and (ii) the algorithm returns no if the oracle returns no.
NP means the class of all decision problems where “yes” answers can be verified efficiently[7, 10th slide]. It is a property regarding only decision problems. Therefore, we can show that TSP-DEC is NP-complete. However, we can never say TSP-OPT is NP-complete [10].
The proof of TSP-DEC is NP-complete can be found: [6], [8], [9]. The basic idea is to reduce from Hamiltonian-cycle problem which is known to be NP-complete.
Similarly, there are many tutorials on proving independent-set problem is a NP-complete problem [4, 5].
Although we can’t say TSP-OPT is NP-complete because it is not even a decision problem, we can say TSP-OPT is a NP-hard problem because TSP-OPT is self reducible from TSP-DEC. From a reply from [10]:
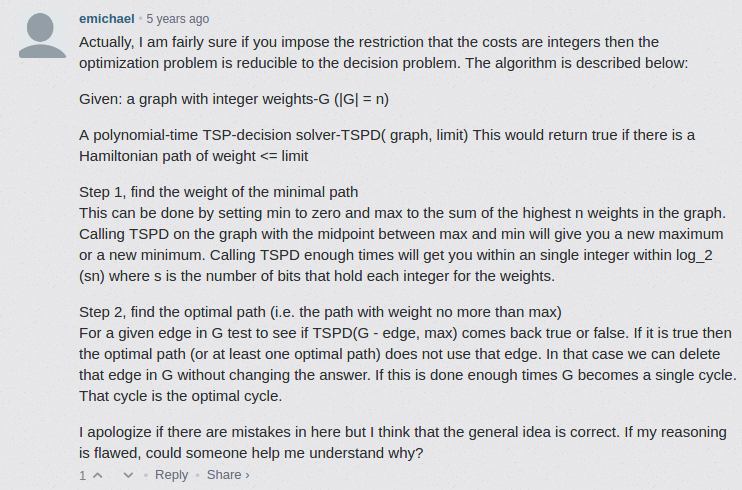
This means, TSP-OPT can be solved just in polynomial scale of the time solving TSP-DEC.
More words about self-reducible. A good tutorial of self-reducible can be found in [11, 12, 13]. It seems like (I haven’t verified) that “Every NP-Complete problem/language L is self-reducible” (from Theorem 24.3.4 in [12]). That means, all NP-complete optimization problems can be polynomially reducible to their decision problems.
Reference
[1] https://en.wikipedia.org/wiki/Travelling_salesman_problem
[2] http://www.ics.uci.edu/~eppstein/161/960312.html
[3] https://stackoverflow.com/questions/4294270/how-to-prove-that-a-problem-is-np-complete
[4] http://www.cs.cornell.edu/courses/cs482/2004su/handouts/NPComplete.pdf
[5] https://perso.esiee.fr/~mustafan/TechnicalWritings/Complexityslides/lec6.pdf
[6] https://www.quora.com/Why-is-the-traveling-salesman-problem-NP-complete
[7] https://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/19/Small19.pdf
[8] https://www.researchgate.net/file.PostFileLoader.html?id=58a153df40485494272392f9&assetKey=AS%3A461190431285249%401486967775832
[9] https://math.stackexchange.com/questions/1077436/the-traveling-salesman-problem-is-np-complete-reduction
[10] http://www.nomachetejuggling.com/2012/09/14/traveling-salesman-the-most-misunderstood-problem/
[11] http://www.cs.toronto.edu/~fpitt/20109/CSC363/lectures/LN11.txt
[12] https://courses.engr.illinois.edu/cs473/fa2011/lec/24_notes.pdf
[13] https://cseweb.ucsd.edu/~mihir/cse200/decision-search.pdf