Embedding methods have been widely used in graph, network, NLP and recommendation system. In short, embedding methods vectorize entities under study by mapping them into a shared latent space. Once vectorized representation of entities are learned (through either supervised or unsupervised fashion), a lot of knowledge discovery work can be done: clustering based on entity vectors, analyze each dimension of the latent space, make recommendation, so on so forth.
When you learn embedding by supervised learning, you define a objective function that forges interaction of entity vectors and then learn vectors through maximizing/minimizing the objective function. When you learn embedding through unsupervised learning, you define how occurrences of data should conform to a conjured, underlying probability function in terms of entity vectors. This will be elaborated more in the following.
Recommendation System
A widely known embedding method is matrix factorization in recommendation system. Affinity of a user and an item is often modeled as the dot product of the two corresponding entity vectors. When you are given a huge, sparse user-item matrix, you try to learn all user/item vectors such that their dot products can maximally approximate the entries in the sparse matrix. For more information, see [2]
NLP
Embedding in NLP has been rapidly developed recently. Let’s see a few classic embedding NLP models.
[3] published 2003. It tries to predict t-th word given t-1 words previously seen in word sequences. The model extends a neural network model:
- input is horizontal concatenation of input word vectors:
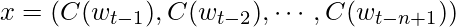
- hidden layer is just a non-linear tanh layer:
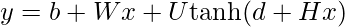
- output layer is a softmax layer. For word
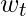that indeed appears after 
: 
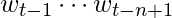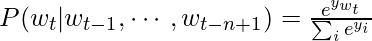
- objective function is to maximize the log-likelihood:
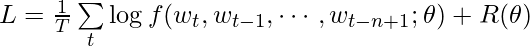
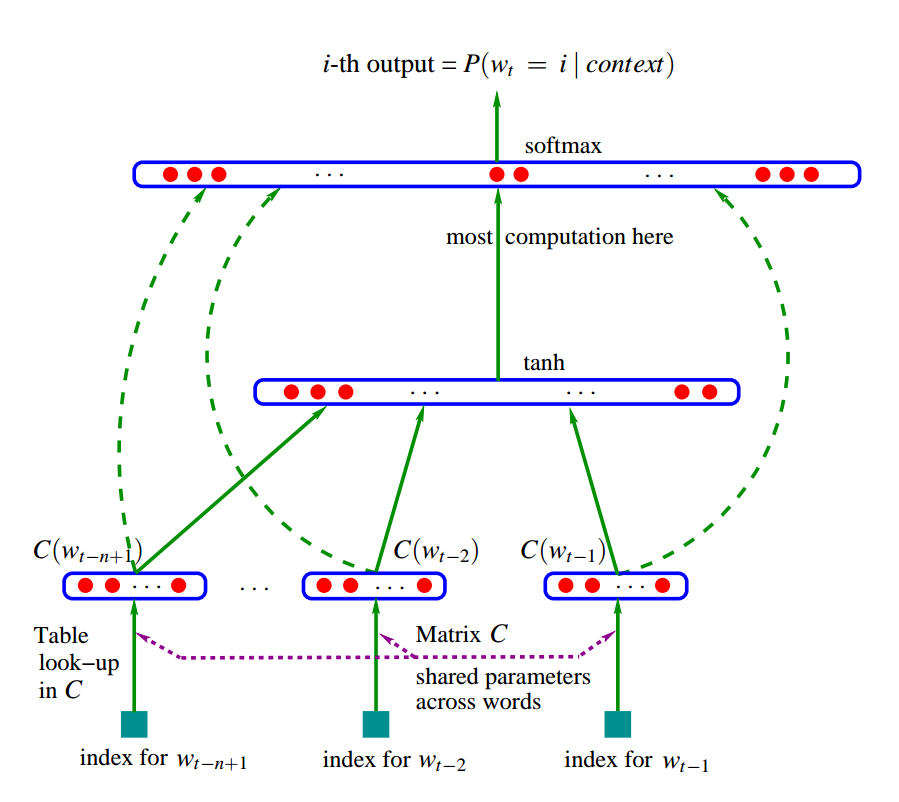
The diagram of the model structure (from the paper [3]):
Equivalently, the model structure from [1]:
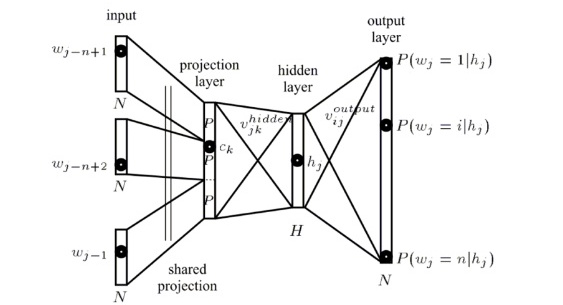
One problem is that in the normalization term in the softmax is expensive when vocabulary size is usually large. In [3], it proposes several parallelism implementation to accelerate learning. The other alternative is using hierarchical softmax [4, 5], which only needs to evaluate 
for each softmax calculation. There are several other more efficient algorithms that are proposed to sidestep the calculation of softmax.
C&W model [17, 18]
C&W model has the following structure:
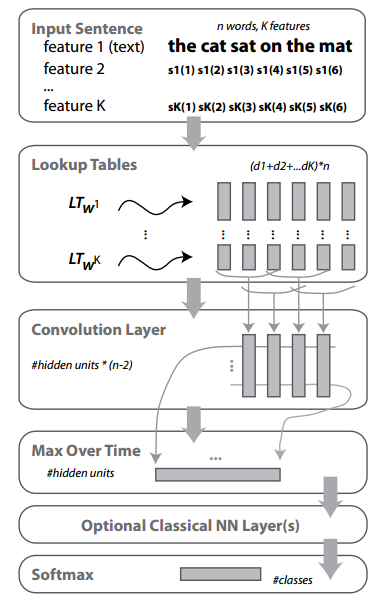
First, a word has multiple features (feature 1 ~ feature K), each has a 
dimension embedding. Then a convolution layer is added to summarize surrounding embedding of each word. Then a max pooling is added so that most salient features will be kept. The last few layers are classic NN layers for supervised learning.
One contribution of the papers is to propose multi-task learning under the same, shared embedding table. The multi-task learning procedure is as follows:
Furthermore, the tasks to be learned can be either supervised or unsupervised. In section 5 of [17], it introduces how to train a language model “to discriminate a two-class classification task”. Note the special ranking-type cost it uses:
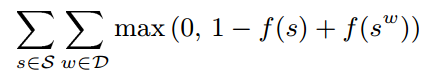
Continuous bag-of-words [5]
This model is easy to understand. Projection layer is no longer the horizontal concatenation of word vectors [3]. Instead we just sum over all input word vectors as the input before the hidden layer.
Skip-gram [6]
Note to differentiate this with [7]. Instead of using a whole sequence to predict the right next word, Skip-gram uses one word to predict its every surrounding word. Specifically, the objective function is:
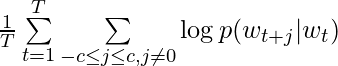
If in every pair of 
, we denote 
as 
and as 
, then we have
However, this objective function suffers the problem we described in [3]: the normalization term in softmax is expensive to calculate because vocabulary is often large. Therefore, they propose to use Negative sampling, which replaces 
in the objective function above with:
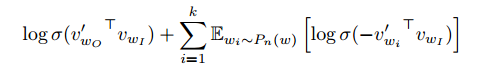
Since we are maximizing the objective function, we can understand it in such intuition: we want 
as large as possible. Therefore, 
and 
should be as similar as possible. On the other hand, the original normalization term in softmax can be seen to be replaced by ![\sum\limits_{i=1}^k \mathbb{E}_{w_i \sim P_n(w)}[\log\sigma({-v'_{w_i}}^T v_{w_I})]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-1cea7eb7c36b01e91574bbeffdafd7a6_l3.png "Rendered by QuickLaTeX.com")
, which contains 
log-sigmoid function smoothing the negative dot products with noisy word vectors. Of course, to maximize it, 
and should be as dissimilar as possible.
Finally, the authors claim that using a modified unigram distribution 
is good in practice. I guess the unigram distribution means each word has the probability mass correlated to the frequencies it appears in the data.
Miscellaneous NLP paper
The following are some papers with less attention so far.
[8] proposes that for each word, its word embedding should be unique across different supervised labels.
[9] proposes that adding more non-linear hidden layers could result in better differentiating ability in bag-of-word model.
For more NLP embedding overview, please see [1].
(Heterogeneous) Network
A heterogeneous network is a graph with multiple types of nodes and links can connect two different types of nodes. Meta-path define a series of links in a heterogeneous network [10, 11]. Heterogeneous network has richer information to harvest compared to single typed network.
[13] first learns embedding of documents, words, and labels. Then, classification .
[14] learns entity embedding (author, paper, keyword, etc) in bibliographical network for the author identification task. The objective function contains two parts: 1. task-specific embedding. author vector should be similar to paper vector which is obtained by averaging vectors per node type. 2. path-augmented heterogeneous network embedding. Two entity vectors should be similar if they are connected by certain meta-path.
[15] models normal events’ happening probabilities as interactions between entity embeddings.
[16] models people’s behavior on twitter to infer their political opinion embeddings. The behavior on twitter is converted to a heterogeneous network where there exist 3 types of links: follow, mention and retweet.
Visualization
T-sne [12] is a dimensionality reduction technology with its goal to “preserve as much of the significant structure of the high dimensional data as possible in the low-dimensional map”. It focus on capturing the local structure of the high-dimensional data very well, while also revealing global structure such as the presence of clusters. To achieve that, t-sne converts pairwise similarity measurement to conditional probability and the objective function is the Kullback-Leibler divergence between conditional probability distribution under original high dimension and transformed low dimension space. It has been widely used for data interpretation in embedding papers.
Reference
[1] http://sebastianruder.com/word-embeddings-1/index.html
[2] https://czxttkl.com/?p=1214
[3] Bengio, Y., Ducharme, R., Vincent, P., & Jauvin, C. (2003). A neural probabilistic language model. journal of machine learning research, 3(Feb), 1137-1155.
[4] Morin, F., & Bengio, Y. (2005, January). Hierarchical Probabilistic Neural Network Language Model. In Aistats (Vol. 5, pp. 246-252).
[5] Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
[6] Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. (2013). Distributed representations of words and phrases and their compositionality. In Advances in neural information processing systems (pp. 3111-3119).
[7] Li, C., N., Wang, B., Pavlu, V., & Aslam, J. Conditional Bernoulli Mixtures for Multi-Label Classification.
[8] Jin, P., Zhang, Y., Chen, X., & Xia, Y. (2016). Bag-of-Embeddings for Text Classification. In International Joint Conference on Artificial Intelligence (No. 25, pp. 2824-2830).
[9] Iyyer, M., Manjunatha, V., Boyd-Graber, J., & Daumé III, H. (2015). Deep unordered composition rivals syntactic methods for text classification. In Proceedings of the Association for Computational Linguistics.
[10] Kong, X., Yu, P. S., Ding, Y., & Wild, D. J. (2012, October). Meta path-based collective classification in heterogeneous information networks. In Proceedings of the 21st ACM international conference on Information and knowledge management (pp. 1567-1571). ACM.
[11] Sun, Y., Han, J., Yan, X., Yu, P. S., & Wu, T. (2011). Pathsim: Meta path-based top-k similarity search in heterogeneous information networks. Proceedings of the VLDB Endowment, 4(11), 992-1003.
[12] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.
[13] Tang, J., Qu, M., & Mei, Q. (2015, August). Pte: Predictive text embedding through large-scale heterogeneous text networks. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 1165-1174). ACM.
[14] Chen, T., & Sun, Y. (2016). Task-Guided and Path-Augmented Heterogeneous Network Embedding for Author Identification. arXiv preprint arXiv:1612.02814.
[15] Chen, T., Tang, L. A., Sun, Y., Chen, Z., & Zhang, K. Entity Embedding-based Anomaly Detection for Heterogeneous Categorical Events.
[16] Gu, Y., Chen, T., Sun, Y., & Wang, B. (2016). Ideology Detection for Twitter Users with Heterogeneous Types of Links. arXiv preprint arXiv:1612.08207.
[17] Collobert, R., & Weston, J. (2008, July). A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th international conference on Machine learning (pp. 160-167). ACM.
[18] Collobert, R., Weston, J., Bottou, L., Karlen, M., Kavukcuoglu, K., & Kuksa, P. (2011). Natural language processing (almost) from scratch. Journal of Machine Learning Research, 12(Aug), 2493-2537.