In the industry there is a trend to add a re-ranker at the final stage of a recommendation system. The re-ranker ranks the items that have already been filtered out from an enormous candidate set, aiming to provide the finest level of personalized ordering before the items are ultimately delivered to the user.
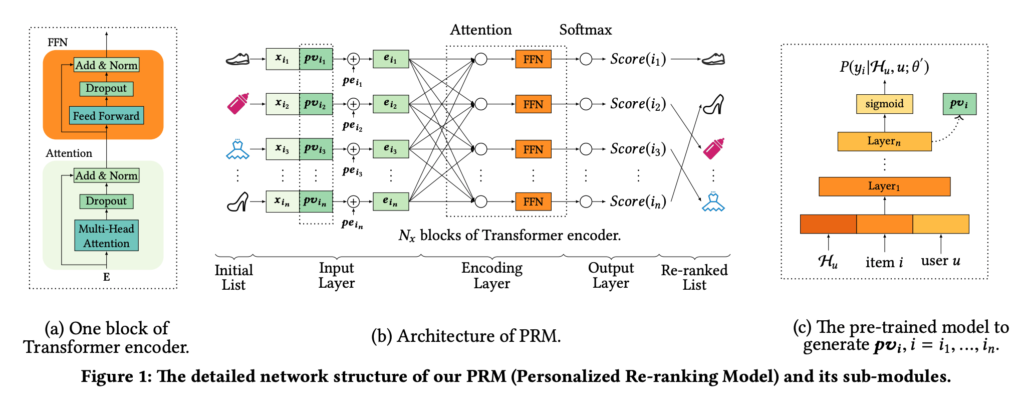
In this post I am trying to have a quick re-implementation of “Personalized Re-ranking for Recommendation” [1]. The model architecture is as follows. A transformer encoder encodes candidate item features and user features, and then attention score is computed for each item (analogous to pairwise ranking). All attention scores will pass through a softmax function and fit with click labels.
import dataclasses
from dataclasses import asdict, dataclass
import torch.nn as nn
from functools import partial, reduce
import torch
import numpy as np
from torch.utils.data import DataLoader, Dataset
import random
from typing import cast
PADDING_SYMBOL = 0
@dataclass
class PreprocessedRankingInput:
state_features: torch.Tensor
src_seq: torch.Tensor
tgt_out_seq: torch.Tensor
slate_reward: torch.Tensor
position_reward: torch.Tensor
tgt_out_idx: torch.Tensor
def _replace(self, **kwargs):
return cast(type(self), dataclasses.replace(self, **kwargs))
def cuda(self):
cuda_tensor = {}
for field in dataclasses.fields(self):
f = getattr(self, field.name)
if isinstance(f, torch.Tensor):
cuda_tensor[field.name] = f.cuda(non_blocking=True)
return self._replace(**cuda_tensor)
def embedding_np(idx, table):
""" numpy version of embedding look up """
new_shape = (*idx.shape, -1)
return table[idx.flatten()].reshape(new_shape)
class TransposeLayer(nn.Module):
def forward(self, input):
return input.transpose(1, 0)
def create_encoder(
input_dim,
d_model=512,
nhead=2,
dim_feedforward=512,
dropout=0.1,
activation="relu",
num_encoder_layers=2,
use_gpu=False,
):
feat_embed = nn.Linear(input_dim, d_model)
encoder_layer = nn.TransformerEncoderLayer(
d_model, nhead, dim_feedforward, dropout, activation
)
encoder_norm = nn.LayerNorm(d_model)
encoder = nn.TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)
scorer = nn.Linear(d_model, 1)
final_encoder = nn.Sequential(
feat_embed,
nn.ReLU(),
TransposeLayer(), # make sure batch_size is the first dim
encoder, # nn.TransformerEncoder assumes batch_size is the second dim
TransposeLayer(),
nn.ReLU(),
scorer
)
if use_gpu:
final_encoder.cuda()
return final_encoder
def _num_of_params(model):
return len(torch.cat([p.flatten() for p in model.parameters()]))
def _print_gpu_mem(use_gpu):
if use_gpu:
print(
'gpu usage',
torch.cuda.memory_stats(
torch.device('cuda')
)['active_bytes.all.current'] / 1024 / 1024 / 1024,
'GB',
)
def create_nn(
input_dim,
d_model=512,
nhead=8,
dim_feedforward=512,
dropout=0.1,
activation="relu",
num_encoder_layers=2,
use_gpu=False,
):
feat_embed = nn.Linear(input_dim, d_model)
scorer = nn.Linear(d_model, 1)
final_nn = nn.Sequential(
feat_embed,
nn.ReLU(),
nn.Linear(d_model, d_model),
nn.ReLU(),
nn.Linear(d_model, d_model),
nn.ReLU(),
scorer,
)
if use_gpu:
final_nn.cuda()
return final_nn
def batch_to_score(encoder, batch, test=False):
batch_size, tgt_seq_len = batch.tgt_out_idx.shape
state_feat_dim = batch.state_features.shape[1]
concat_feat_vec = torch.cat(
(
batch.state_features.repeat(1, max_src_seq_len).reshape(
batch_size, max_src_seq_len, state_feat_dim
),
batch.src_seq,
),
dim=2,
)
encoder_output = encoder(concat_feat_vec).squeeze(-1)
if test:
return encoder_output
device = encoder_output.device
slate_encoder_output = encoder_output[
torch.arange(batch_size, device=device).repeat_interleave(tgt_seq_len),
batch.tgt_out_idx.flatten(),
].reshape(batch_size, tgt_seq_len)
return slate_encoder_output
def train(encoder, batch, optimizer):
# shape: batch_size, tgt_seq_len
slate_encoder_output = batch_to_score(encoder, batch)
log_softmax = nn.LogSoftmax(dim=1)
kl_loss = nn.KLDivLoss(reduction="batchmean")
loss = kl_loss(log_softmax(slate_encoder_output), batch.position_reward)
optimizer.zero_grad()
loss.backward()
optimizer.step()
return loss.detach().cpu().numpy()
@torch.no_grad()
def test(encoder, batch):
encoder.eval()
# shape: batch_size, tgt_seq_len
slate_encoder_output = batch_to_score(encoder, batch, test=False)
slate_acc = torch.mean(
(
torch.argmax(slate_encoder_output, dim=1)
== torch.argmax(batch.position_reward, dim=1)
).float()
)
# shape: batch_size, seq_seq_len
total_encoder_output = batch_to_score(encoder, batch, test=True)
batch_size = batch.tgt_out_idx.shape[0]
correct_idx = batch.tgt_out_idx[
torch.arange(batch_size), torch.argmax(batch.position_reward, dim=1)
]
total_acc = torch.mean(
(
torch.argmax(total_encoder_output, dim=1)
== correct_idx
).float()
)
encoder.train()
print(f"slate acc {slate_acc}, total acc {total_acc}")
class ValueModel(nn.Module):
"""
Generate ground-truth VM coefficients based on user features + candidate distribution
"""
def __init__(self, state_feat_dim, candidate_feat_dim, hidden_size):
super(ValueModel, self).__init__()
self.state_feat_dim = state_feat_dim
self.candidate_feat_dim = candidate_feat_dim
self.hidden_size = hidden_size
self.layer1 = nn.Linear(state_feat_dim + 3 * candidate_feat_dim, candidate_feat_dim)
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
# model will be called with fixed parameters
p.requires_grad = False
def forward(
self,
state_features,
src_seq,
tgt_out_seq,
tgt_out_idx,
):
batch_size, max_src_seq_len, candidate_feat_dim = src_seq.shape
max_tgt_seq_len = tgt_out_seq.shape[1]
mean = src_seq.mean(dim=1)
std = src_seq.std(dim=1)
max = src_seq.max(dim=1).values
vm_coef = self.layer1(torch.cat((state_features, mean, std, max), dim=1)).unsqueeze(2)
pointwise_score = torch.bmm(tgt_out_seq, vm_coef).squeeze()
return pointwise_score
class TestDataset(Dataset):
def __init__(
self,
batch_size: int,
num_batches: int,
state_feat_dim: int,
candidate_feat_dim: int,
max_src_seq_len: int,
max_tgt_seq_len: int,
use_gpu: bool,
):
self.batch_size = batch_size
self.num_batches = num_batches
self.state_feat_dim = state_feat_dim
self.candidate_feat_dim = candidate_feat_dim
self.max_src_seq_len = max_src_seq_len
self.max_tgt_seq_len = max_tgt_seq_len
self.use_gpu = use_gpu
self.personalized_vm = ValueModel(state_feat_dim, candidate_feat_dim, 10)
if use_gpu:
self.personalized_vm.cuda()
def __len__(self):
return self.num_batches
def action_generator(self, state_features, src_seq):
batch_size, max_src_seq_len, _ = src_seq.shape
action = np.full((batch_size, self.max_tgt_seq_len), PADDING_SYMBOL).astype(np.long)
for i in range(batch_size):
action[i] = np.random.permutation(
np.arange(self.max_src_seq_len)
)[:self.max_tgt_seq_len]
return action
def reward_oracle(
self,
state_features,
src_seq,
tgt_out_seq,
tgt_out_idx,
):
batch_size = state_features.shape[0]
# shape: batch_size x max_tgt_seq_len
pointwise_score = self.personalized_vm(
state_features,
src_seq,
tgt_out_seq,
tgt_out_idx,
)
slate_rewards = torch.ones(batch_size)
position_rewards = (
pointwise_score == torch.max(pointwise_score, dim=1).values.unsqueeze(1)
).float()
return slate_rewards, position_rewards
@torch.no_grad()
def __getitem__(self, idx):
if self.use_gpu:
device = torch.device("cuda")
else:
device = torch.device("cpu")
if idx % 10 == 0:
print(f"generating {idx}")
_print_gpu_mem(self.use_gpu)
candidate_feat_dim = self.candidate_feat_dim
state_feat_dim = self.state_feat_dim
batch_size = self.batch_size
max_src_seq_len = self.max_src_seq_len
max_tgt_seq_len = self.max_tgt_seq_len
state_features = np.random.randn(batch_size, state_feat_dim).astype(np.float32)
candidate_features = np.random.randn(
batch_size, self.max_src_seq_len, candidate_feat_dim
).astype(np.float32)
# The last candidate feature is the sum of all other features. This just
# simulates that in prod we often have some computed scores based on
# the raw features
candidate_features[:, :, -1] = np.sum(candidate_features[:, :, :-1], axis=-1)
tgt_out_idx = np.full((batch_size, max_tgt_seq_len), PADDING_SYMBOL).astype(
np.long
)
src_seq = np.zeros((batch_size, max_src_seq_len, candidate_feat_dim)).astype(
np.float32
)
tgt_out_seq = np.zeros(
(batch_size, max_tgt_seq_len, candidate_feat_dim)
).astype(np.float32)
for i in range(batch_size):
# TODO: we can test sequences with different lengths
src_seq_len = max_src_seq_len
src_in_idx = np.arange(src_seq_len)
src_seq[i] = embedding_np(src_in_idx, candidate_features[i])
with torch.no_grad():
tgt_out_idx = self.action_generator(state_features, src_seq)
for i in range(batch_size):
tgt_out_seq[i] = embedding_np(tgt_out_idx[i], candidate_features[i])
with torch.no_grad():
slate_rewards, position_rewards = self.reward_oracle(
torch.from_numpy(state_features).to(device),
torch.from_numpy(src_seq).to(device),
torch.from_numpy(tgt_out_seq).to(device),
torch.from_numpy(tgt_out_idx).to(device),
)
slate_rewards = slate_rewards.cpu()
position_rewards = position_rewards.cpu()
return PreprocessedRankingInput(
state_features=torch.from_numpy(state_features),
src_seq=torch.from_numpy(src_seq),
tgt_out_seq=torch.from_numpy(tgt_out_seq),
slate_reward=slate_rewards,
position_reward=position_rewards,
tgt_out_idx=torch.from_numpy(tgt_out_idx),
)
def _collate_fn(batch):
assert len(batch) == 1
return batch[0]
def _set_np_seed(worker_id):
np.random.seed(worker_id)
random.seed(worker_id)
@torch.no_grad()
def create_data(
batch_size,
num_batches,
max_src_seq_len,
max_tgt_seq_len,
state_feat_dim,
candidate_feat_dim,
num_workers,
use_gpu,
):
dataset = DataLoader(
TestDataset(
batch_size,
num_batches,
state_feat_dim,
candidate_feat_dim,
max_src_seq_len,
max_tgt_seq_len,
use_gpu=use_gpu,
),
batch_size=1,
shuffle=False,
num_workers=num_workers,
worker_init_fn=_set_np_seed,
collate_fn=_collate_fn,
)
dataset = [batch for i, batch in enumerate(dataset)]
return dataset
def main(
dataset,
create_model_func,
num_epochs,
state_feat_dim,
candidate_feat_dim,
use_gpu,
):
model = create_model_func(
input_dim=state_feat_dim + candidate_feat_dim, use_gpu=use_gpu
)
print(f"model num of params: {_num_of_params(model)}")
optimizer = torch.optim.Adam(
model.parameters(), lr=0.001, amsgrad=True,
)
test_batch = None
for e in range(num_epochs):
epoch_loss = []
for i, batch in enumerate(dataset):
if use_gpu:
batch = batch.cuda()
if e == 0 and i == 0:
test_batch = batch
test(model, test_batch)
print()
continue
loss = train(model, batch, optimizer)
epoch_loss.append(loss)
if (e == 0 and i < 10) or i % 10 == 0:
print(f"epoch {e} batch {i} loss {loss}")
test(model, test_batch)
print()
print(f"epoch {e} average loss: {np.mean(epoch_loss)}\n")
return model
if __name__ == "__main__":
batch_size = 4096
num_batches = 100
max_src_seq_len = 10
max_tgt_seq_len = 5
state_feat_dim = 7
candidate_feat_dim = 10
num_workers = 0
use_gpu = True
dataset = create_data(
batch_size,
num_batches,
max_src_seq_len,
max_tgt_seq_len,
state_feat_dim,
candidate_feat_dim,
num_workers,
use_gpu,
)
num_epochs = 10
encoder = main(
dataset,
create_encoder,
num_epochs,
state_feat_dim,
candidate_feat_dim,
use_gpu,
)
num_epochs = 10
nnet = main(
dataset,
create_nn,
num_epochs,
state_feat_dim,
candidate_feat_dim,
use_gpu,
)
Code explanation:
We create `TestDataset` to generate random data. Here I create a hypothetical situation where we have state features (user features) and src_seq, which are the features of candidates and the input to the encoder. tgt_out_seq are the features of the items actually shown to the user.
For each ranking data point, the user will click the best item, as you can see in `reward_oracle` function. The best item of the ground truth is determined by a value model, which computes item scores based on user features and the characteristics of candidate features (mean, max, and standard deviation of the candidate distribution).
In `train` function, you can see that we use KLDivLoss to fit attention scores against position_rewards (clicks as mentioned above).
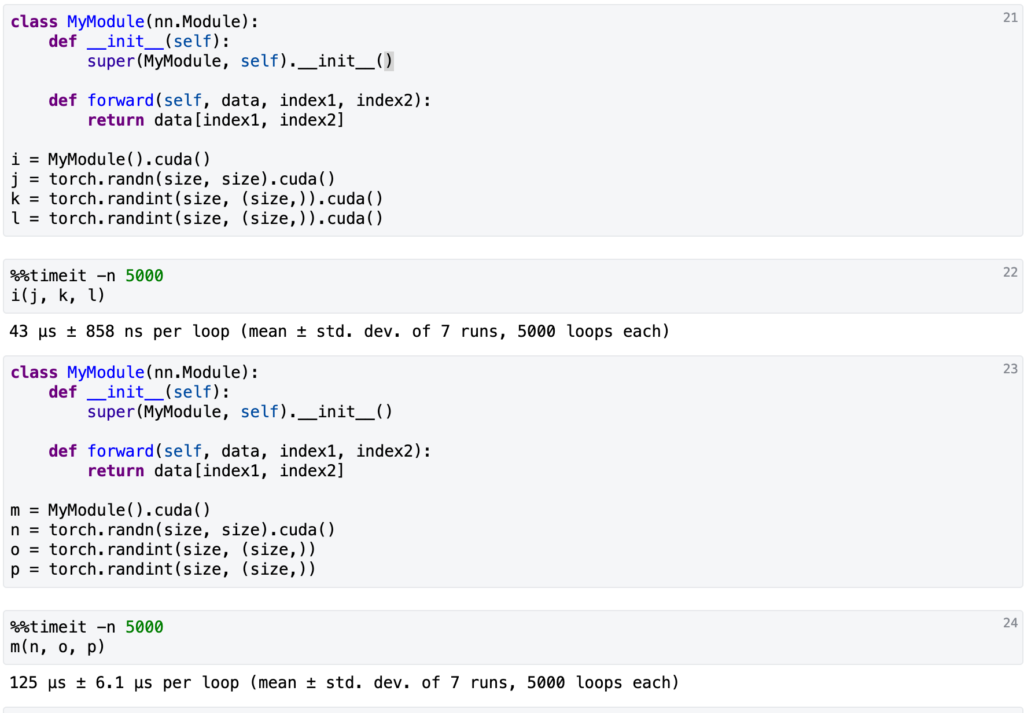
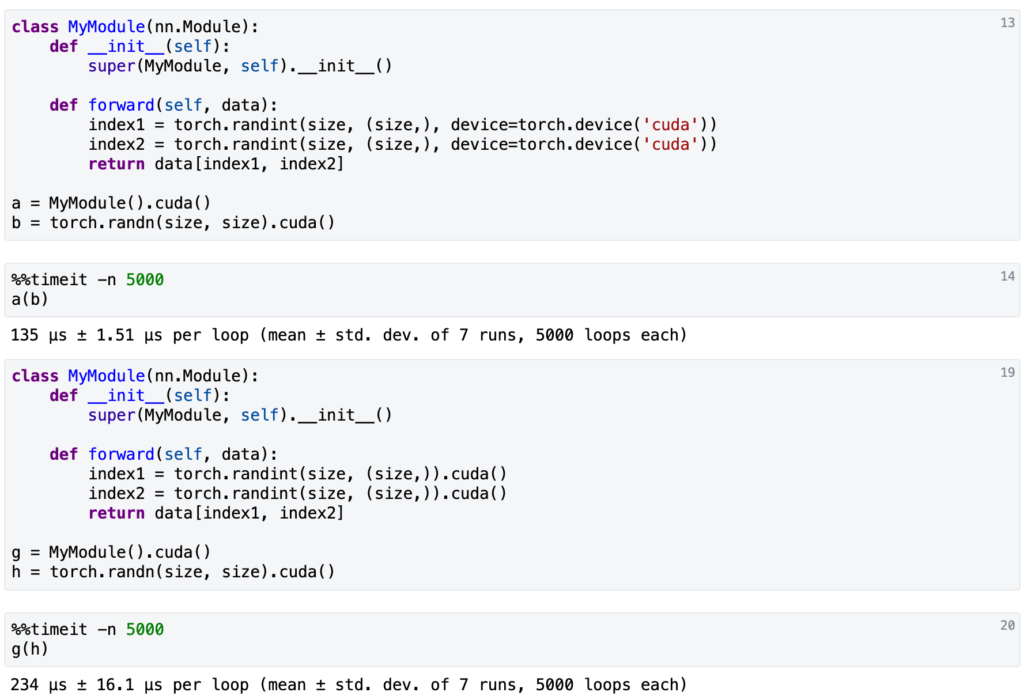
In `test` function , we test how many times the best item resulted from the encoder model is the same as the ground truth.
We also compare the transformer encoder with a classic multi-layer NN.
Final outputs:
Transformer encoder output:
epoch 9 batch 90 loss 0.24046754837036133
slate acc 0.92333984375
epoch 9 average loss: 0.23790153861045837
NN output:
epoch 9 batch 90 loss 0.6537740230560303
slate acc 0.73583984375
epoch 9 average loss: 0.6661167740821838
As we can see, the transformer encoder model clearly outperforms the NN in slate acc.
References
[1] Personalized Re-ranking for Recommendation
![Rendered by QuickLaTeX.com J(\theta)\newline=\mathbb{E}_{s,a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)] \newline=\mathbb{E}_{s \sim \pi_\theta}[ \mathbb{E}_{a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)]]\newline=\mathbb{E}_{s\sim\pi_\theta} [\int \pi_\theta(a|s) Q^{\pi_\theta}(s,a) da]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-f1469552882502e8a85fcd638aa96963_l3.png)
![Rendered by QuickLaTeX.com \nabla_{\theta} J(\theta) \newline= \mathbb{E}_{s\sim\pi_\theta} [\int \nabla \pi_\theta(a|s) Q^{\pi_\theta}(s,a) da] \quad\quad \text{Treat } Q^{\pi_\theta}(s,a) \text{ as non-differentiable} \newline= \mathbb{E}_{s\sim\pi_\theta} [\int \pi_\theta(a|s) \frac{\nabla \pi_\theta(a|s)}{\pi_\theta(a|s)} Q^{\pi_\theta}(s,a) da] \newline= \mathbb{E}_{s, a \sim \pi_\theta} [Q^{\pi_\theta}(s,a) \nabla_\theta log \pi_\theta(a|s)] \newline \approx \frac{1}{N} [G_t \nabla_\theta log \pi_\theta(a_t|s_t)] \quad \quad s_t, a_t \sim \pi_\theta](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-f73caef052359dd2ab0ff34a060164b9_l3.png)
![Rendered by QuickLaTeX.com J(\theta)\newline=\mathbb{E}_{s\sim\pi_b}\left[\mathbb{E}_{a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)] \right] \newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\pi_\theta(a|s)}{\pi_b(a|s)}Q^{\pi_b}(s,a)]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-99250c6e14614db890a3fe8e8487be7e_l3.png)
![Rendered by QuickLaTeX.com \nabla_{\theta} J(\theta) \newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\nabla_\theta \pi_\theta(a|s)}{\pi_b(a|s)} Q^{\pi_b}(s,a)] \quad\quad \text{Again, treat } Q^{\pi_b}(s,a) \text{ as non-differentiable}\newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\pi_\theta(a|s)}{\pi_b(a|s)} Q^{\pi_b}(s,a) \nabla_\theta log \pi_\theta(a|s)] \newline \approx \frac{1}{N}[\frac{\pi_\theta(a_t|s_t)}{\pi_b(a_t|s_t)} G_t \nabla_\theta log \pi_\theta(a_t|s_t)] \quad\quad s_t, a_t \sim \pi_b](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-6861dae8d1e302c9bcfc3d06cac970b0_l3.png)
![Rendered by QuickLaTeX.com \mathbb{E}_{s,a \sim \pi_b} \left[\frac{\pi_\theta(a|s)}{\pi_b(a|s)} b(s) \nabla_\theta log \pi_\theta(a|s)\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \cdot \mathbb{E}_{a \sim \pi_b}\left[\frac{\pi_\theta(a|s)}{\pi_b(a|s)} \nabla_\theta log \pi_\theta(a|s)\right]\right] \newline = \mathbb{E}_{s \sim \pi_b}\left[b(s) \int \pi_b(a|s) \nabla_\theta \frac{\pi_\theta(a|s)}{\pi_b(a|s)} da\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \int \nabla_\theta \pi_\theta(a|s) da\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \nabla_\theta \int \pi_\theta(a|s) da\right] \newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \nabla_\theta 1 \right] \newline=0](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-ccc9f1f74889590d36787146035b678d_l3.png)

![Rendered by QuickLaTeX.com \nabla_\theta \mathbb{E}_{\pi \sim p_\theta(\cdot|x)} \left[ \mathcal{L}_\pi(\theta)\right] \newline= \nabla_\theta \sum\limits_\pi p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\newline=\sum\limits_\pi \left[ \nabla_\theta p_\theta(\pi|x) \cdot \mathcal{L}_\pi(\theta)+p_\theta(\pi|x) \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=p_b(\pi|x) \cdot \sum\limits_\pi \left[ \frac{\nabla_\theta p_\theta(\pi|x)}{p_b(\pi|x)} \cdot \mathcal{L}_\pi(\theta)+\frac{p_\theta(\pi|x)}{p_b(\pi|x)} \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=\mathbb{E}_{\pi\sim p_b(\cdot|x)}\left[\frac{1}{p_b(\pi|x)}\nabla_\theta\left(p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\right)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-227f028e4d3bc7f11df8cb44f48f3e17_l3.png)
![Rendered by QuickLaTeX.com \nabla_\theta \mathbb{E}_{\pi \sim p_\theta(\cdot|x)} \left[ \mathcal{L}_\pi(\theta)\right] \newline= \nabla_\theta \sum\limits_\pi p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\newline=\sum\limits_\pi \left[ \nabla_\theta p_\theta(\pi|x) \cdot \mathcal{L}_\pi(\theta)+p_\theta(\pi|x) \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=p_\theta(\pi|x) \cdot \sum\limits_\pi \left[ \frac{\nabla_\theta p_\theta(\pi|x)}{p_\theta(\pi|x)} \cdot \mathcal{L}_\pi(\theta)+\frac{p_\theta(\pi|x)}{p_\theta(\pi|x)} \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=\mathbb{E}_{\pi\sim p_\theta(\cdot|x)}\left[\frac{1}{p_\theta(\pi|x)}\nabla_\theta\left(p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\right)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-907143278650354a5e362762565099f1_l3.png)
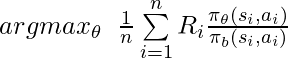
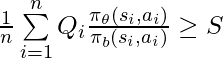
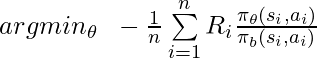
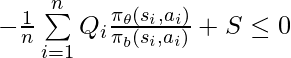
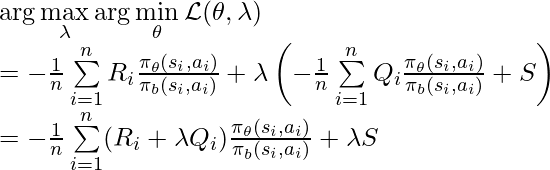
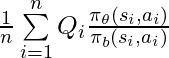 would have a monotonic trend:
would have a monotonic trend: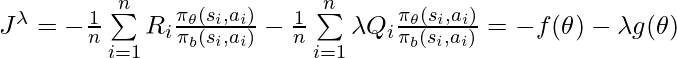





 Now if we want to search if key 361 exists, it will start from index 6 (666). Without the extra bits, we will probe denoted until index 1 (the probe will pass slot 4 pretending it is a full slot). But with the extra bit, we will only need to probe until index 4. At index 4, we know no more key that sharing the same probe path has inserted beyond this point.
Now if we want to search if key 361 exists, it will start from index 6 (666). Without the extra bits, we will probe denoted until index 1 (the probe will pass slot 4 pretending it is a full slot). But with the extra bit, we will only need to probe until index 4. At index 4, we know no more key that sharing the same probe path has inserted beyond this point. 

![Rendered by QuickLaTeX.com \eta(\pi)=\mathbb{E}_{s_0, a_0, \cdots}[\sum\limits_{t=0}^{\infty}\gamma^t r(s_t)]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-7aaa56488dc12ec0dfe3ddf7febd9a8e_l3.png) . The return of another policy
. The return of another policy 
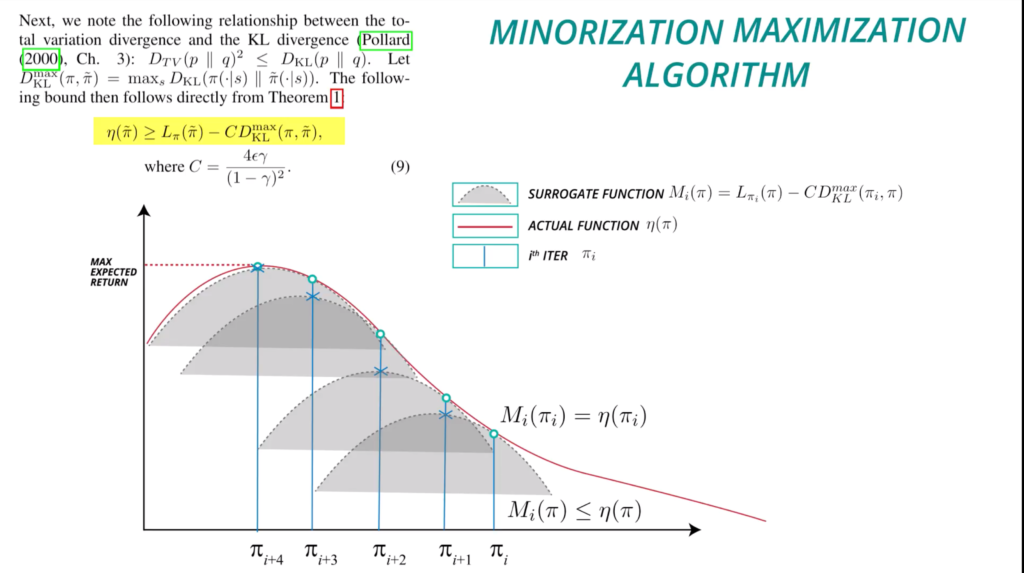
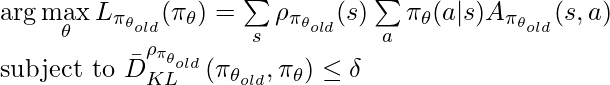
![Rendered by QuickLaTeX.com \arg\max\limits_{\theta} \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \big[\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} Q_{\pi_{\theta_{old}}}(s,a)\big] \newline \text{subject to } \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}} \big[D_{KL}(\pi_{\theta_{old}}(\cdot|s) \| \pi_{\theta}(\cdot|s))\big]\leq \delta](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9a1fda6467b2fce611cb38f03ebe4150_l3.png)
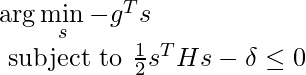
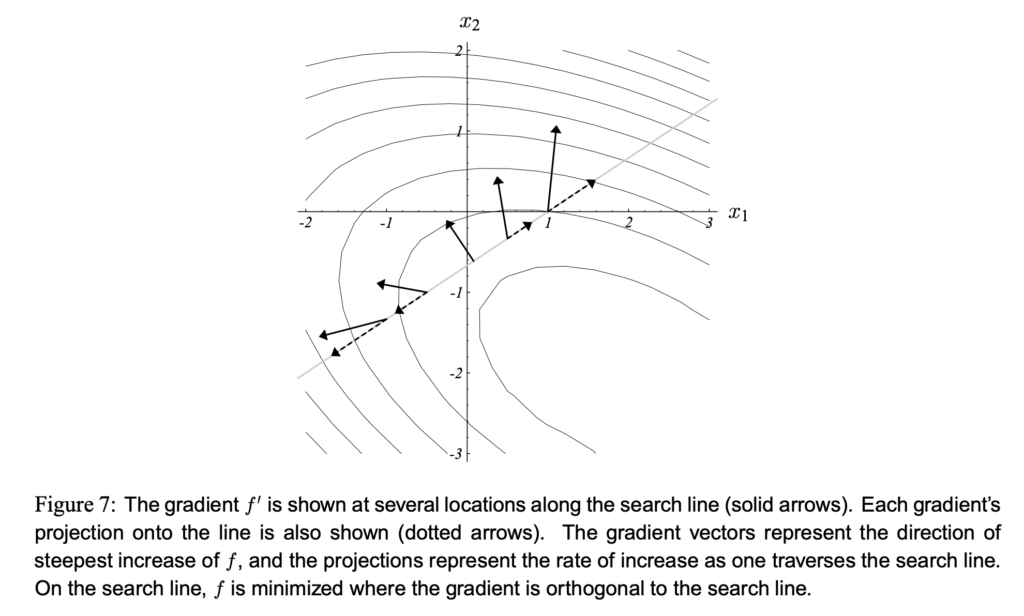
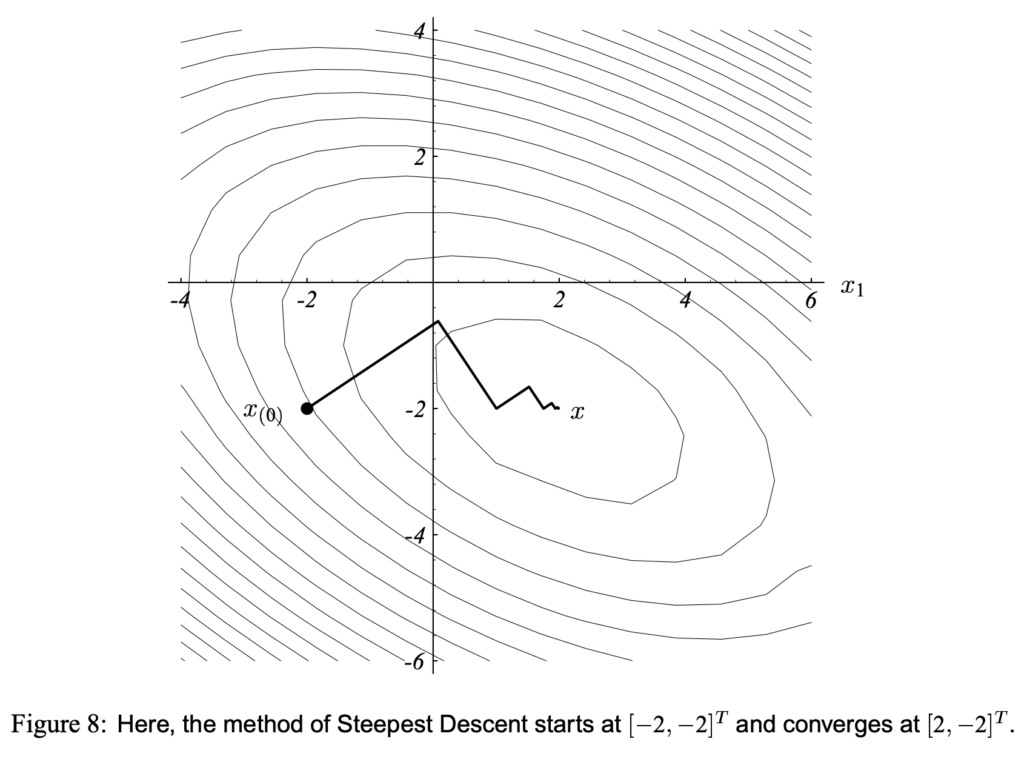
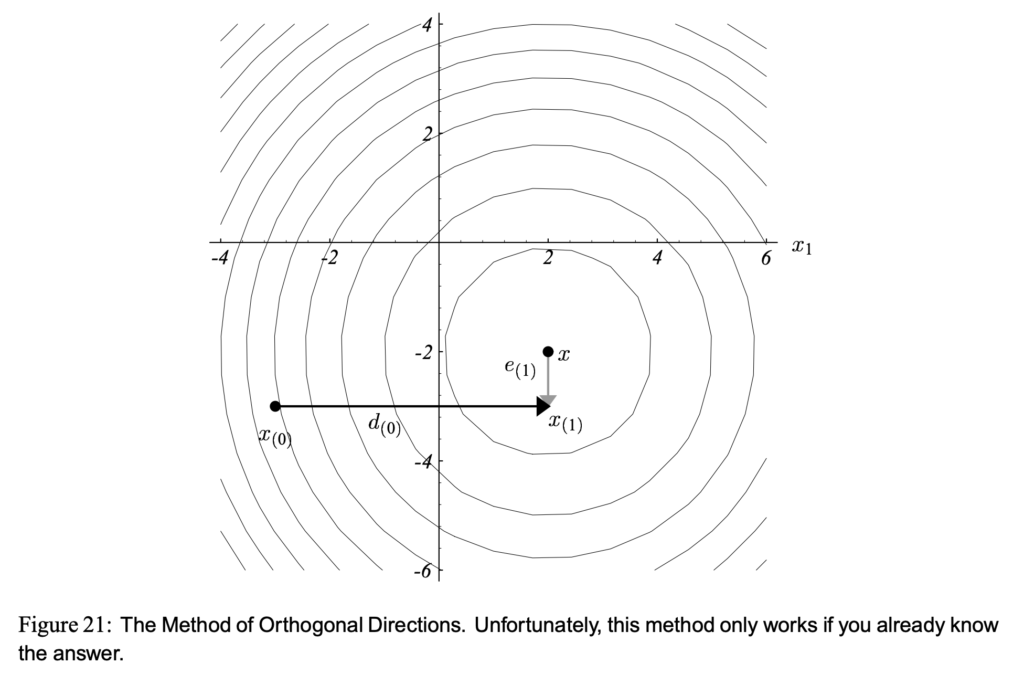

![Rendered by QuickLaTeX.com L^{CLIP}\newline=CLIP\left(\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} A_{\pi_{\theta_{old}}}(s,a)\right]\right)\newline=CLIP\left(\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[r(\theta)A_{\pi_{\theta_{old}}}(s,a)\right]\right)\newline=\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[min(r(\theta), clip(r(\theta), 1-\epsilon, 1+\epsilon)) \cdot A_{\pi_{\theta_{old}}}(s,a)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-7a88ae62a682d12e908cfc57b8527b5d_l3.png)


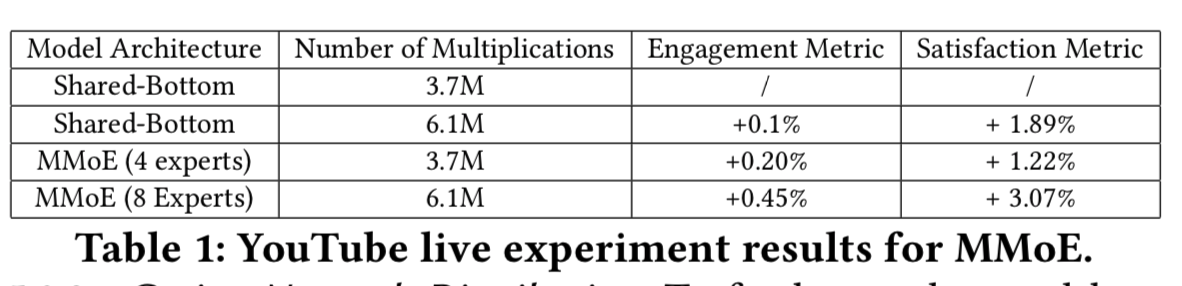

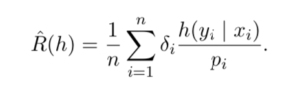
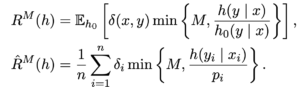
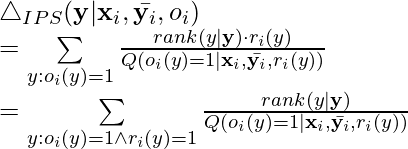 ,
,