Optimization with discrete random variables

In this post, I’m going to talk about common techniques that enable us to optimize a loss function w.r.t. discrete random variables. I may go off on a tangent on various models (e.g., variational auto-encoder and reinforcement learning) because these techniques come from many different areas so please bear with me.

We start from variational auto encoder (VAE) with continuous latent variables. Then we will look at VAE with discrete latent variables.

VAE

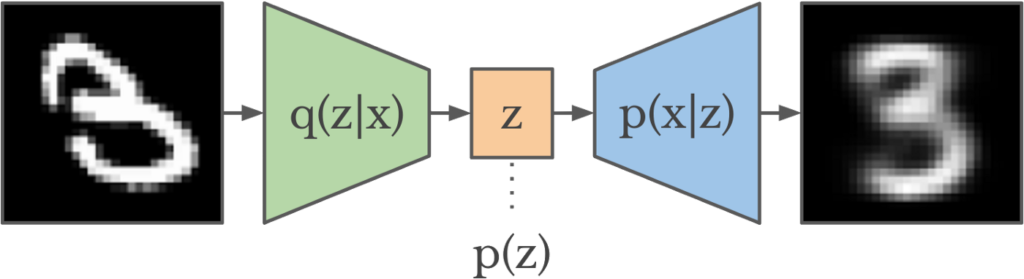
With generative modeling in mind, we suppose every data $x$ is generated by some latent variable $z$ , which itself is a random variable following certain distribution $p(z|x)$ . We’d like to use a parameterized distribution $q_\theta(z|x)$ to approximate $p(z|x)$ (this is the encoder of VAE). Usually, $q_\theta(z|x)$ can be parameterized as a Gaussian distribution: $q_\theta(z|x) \sim \mathcal{N}\left(\mu_\theta(x), \Sigma_\theta(x)\right)$ . To make $p(z|x)$ and $q_\theta(z|x)$ close to each other, we minimize the KL-divergence between them:

$\theta^* = argmin_\theta\; KL\left(q_\theta(z|x) || p(z|x) \right ) \newline= argmin_\theta \; \mathbb{E}_{q_\theta} [log\;q_\theta(z|x)] - \mathbb{E}_{q_\theta} [log\;p(z,x)]+log\;p(x)$

In the formula above, $\mathbb{E}_{q_\theta}[f(z)]$ means $\int q_\theta(z|x) f(z) dz$ , and $log \; p(x)$ is a constant w.r.t. $\theta$ and thus can be omitted. With simple re-arrangement, we can equivalently maximize the so-called ELBO function in order to find $\theta^*$ :

$ELBO(\theta) \newline= \mathbb{E}_{q_\theta} [log\;p(z,x)] - \mathbb{E}_{q_\theta} [log\;q_\theta(z|x)]\newline=\mathbb{E}_{q_\theta}[log\;p(x|z)] + \mathbb{E}_{q_\theta}[log\;p(z)] - \mathbb{E}_{q_\theta}[log\;q_\theta(z|x)] \quad\quad p(z) \text{ is the prior of } z \newline= \mathbb{E}_{q_\theta}[log\;p(x|z)] - \mathbb{E}_{q_\theta} [log \frac{q_{\theta}(z|x)}{p(z)}]\newline=\mathbb{E}_{q_\theta}[log\;p(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)$

Practically, $p(x|z)$ is also fitted by a parameterized function $p_\phi(x|z)$ (this is the decoder of VAE). So the ultimate objective function we have for fitting a VAE is:

(1) $\begin{equation*} $argmax_{\theta, \phi} \; \mathbb{E}_{x\sim D} \left[\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)\right]$\end{equation*}$

We can interpret the objective function in the following ways: $\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)]$ can be thought as the so-called “reconstruction error”, which encourages the reconstructed $x$ be as close to the original $x$ as possible. $KL\left(q_\theta(z|x) || p(z)\right)$ encourages $q_\theta(z|x)$ to be close to the prior of $z$ . For more about ELBO and variational inference, please refer to one older post [8].

——————– Update 09/16/2021 ———————

A good post overviewing VAE: https://stats.stackexchange.com/a/315613/80635

Optimize VAE

Optimizing Eq.1 requires additional care. If using stochastic gradient descent, you might want to first sample an $x$ from the data distribution $D$ , then sample $z$ from $q_\theta(z|x)$ , to compute:

(2) $\begin{equation*} $log\;p_\phi(x|z) - KL\left(q_\theta(z|x) || p(z)\right)$\end{equation*}$

However, Eq.2 is not the Monte Carlo sampling of the real gradient w.r.t. $\theta$ . This is because $\mathbb{E}_{q_\theta}$ in Eq.1 also depends on the learning parameter $\theta$ . Now we introduce two general ways to optimize Eq.1 [1].

The first method is called score function estimator. From now on, we will ignore the part $\mathbb{E}_{x\sim D}$ . The gradient of Eq.1 w.r.t. $\theta$ can be written as:

(3) $\begin{align*}&\nabla_\theta \left\{\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)\right\}\\=&\nabla_\theta \left\{\mathbb{E}_{q_\theta}\left[log\;p_\phi(x, z) - \log q_\theta(z|x)\right] \right\} \quad\quad \text{ rewrite KL divergence} \\ =&\nabla_\theta \; \int q_\theta(z|x) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]dz \\=& \int \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]\nabla_\theta q_\theta(z|x) dz + \int q_\theta(z|x) \nabla_\theta \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] dz \\=& \mathbb{E}_{q_\theta}\left[ \left(log\;p_\phi(x, z) - \log q_\theta(z|x) \right) \nabla_\theta \log q_\theta(z|x) \right] + \mathbb{E}_{q_\theta}\left[\nabla_\theta \log p_\phi(x, z)\right] + \mathbb{E}_{q_\theta}\left[ \nabla_\theta \log q_\theta(z|x) \right] \\&\text{--- The second term is zero because no }\theta \text{ in } \log p_\phi(x,z) \\&\text{--- The third term being zero is a common trick. See Eqn. 5 in [1]} \\=& \mathbb{E}_{q_\theta}\left[ \left(log\;p_\phi(x, z) - \log q_\theta(z|x) \right) \nabla_\theta \log q_\theta(z|x) \right]\end{align*}$

Now we’ve moved the derivative inside the expectation so we can sample $z$ from $q_\theta(z|x)$ to get Monte Carlo sampling of the gradient.

The second method to optimize Eqn. 1 is called pathwise gradient estimator using the reparameterization trick. We’ve seen the trick used in Soft Actor Critic [9]. Here is how Eqn. 1 can be rewritten with the assumption that $z \sim f_\theta(x) + p(\epsilon)$ ( $\epsilon$ is an independent source of noise):

(4) $\begin{align*}&\nabla_\theta \left\{\mathbb{E}_{q_\theta}[log\;p_\phi(x|z)] - KL\left(q_\theta(z|x) || p(z)\right)\right\}\\=&\nabla_\theta \left\{\mathbb{E}_{q_\theta}\left[log\;p_\phi(x, z) - \log q_\theta(z|x)\right] \right\} \quad\quad \text{ rewrite KL divergence} \\=&\nabla_\theta \; \int q_\theta(z|x) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]dz \\=&\nabla_\theta \; \int p(\epsilon) \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]d\epsilon \quad\quad \\&\text{--- Above uses the property of changing variables in probability density functions.} \\&\text{--- See discussion in [10, 11]} \\=& \int p(\epsilon) \nabla_\theta \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right]d\epsilon \\=& \int p(\epsilon) \nabla_z \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] \nabla_\theta z d\epsilon \\=& \mathbb{E}_{p(\epsilon)} \left[ \nabla_z \left[log\;p_\phi(x, z) - \log q_\theta(z|x) \right] \nabla_\theta f_\theta(x) \right]\end{align*}$

I think [1] summarizes really well that the pathwise estimator generally has lower variance in practice:

In the end, I’d like to share a course which covers more topics on optimization with discrete random variables [6].

Optimize Discrete VAE

The idea of discrete VAE is that the hidden variables are represented as discrete random variables such that it could be better understood by humans as clustering of data. The question remains on how you perform reparameterization trick if $z$ is a discrete random variable. The answer is to rely on Gumbel-Softmax trick [12].

Suppose a discrete random variable $z$ has $K$ classes with class probability $\pi_1, \pi_2, \cdots, \pi_k$ , which can be parameterized by a neural network consuming the raw data. There are several steps to perform the Gumbel-Softmax trick. First, $z$ is represented as a one-hot encoding vector. The active component would be the one with the highest following quantity:

(5) $\begin{align*}\arg\max_i \left[ g_i + log \pi_i \right]\end{align*}$

The beauty of Eqn.5 is that this is equivalent to draw a sample based on the probability distribution $\pi_1, \pi_2, \cdots, \pi_k$ .

Second, the one-hot encoding vector is relaxed to a continuous vector $y \in \mathbb{R}^k$ , with each component as:

(6) $\begin{align*}y_i = \frac{exp\left( (log \pi_i + g_i) / \tau \right)}{\sum^k_{j=1} exp \left( (log\pi_j + g_j) / \tau \right)},\end{align*}$

where $g_1, \cdots, g_k$ are i.i.d. samples drawn from $Gumbel(0,1)$ distribution, and $\tau$ will be annealed through the training such that $y$ will be closer and closer to a one-hot encoding vector.

Finally, depending on specific problems, we will forward $y$ as some differentiable quantity to downstream models (discussed in Section 2.2. in [12]). If the problem is about learning hidden representations, we can have fully connected layers on top of the whole $y$ . If the problem would require sampling discrete actions as in reinforcement learning, in forward pass we would need to sample an action by $\arg\max$ on $y$ while in backward pass we would use Straight-Through operator by approximating $\nabla_\theta z \approx \nabla_\theta y$ .

Here is an example of Gumbel-Softmax trick-based discrete VAE, which I adapted from [13]. In the code, we create 30 10-category random variables as the hidden representation $z$ . As a result, $z$ becomes a 300-dim continuous vector during the training. While in testing (where we create images in data/sample_), we randomly create 30 one-hot encoding vectors of dim 10 as the hidden representation, and ask the decoder to generate images for us.

An earlier attempt to train discrete VAE can be seen in [5] and [3]. It uses embedding table look up + straight through to train such discrete VAE models.

References

[1] Lecture Notes. Part III: Black-Box Variational Inference

[2] http://edwardlib.org/tutorials/klqp

[3] Reproducing Neural Discrete Representation Learning

[4] https://github.com/ritheshkumar95/pytorch-vqvae

[5] Neural Discrete Representation Learning

[6] https://duvenaud.github.io/learn-discrete/

[7] Discrete Variational Autoencoders

[8] https://czxttkl.com/2019/05/04/stochastic-variational-inference/

[9] https://czxttkl.com/2018/10/30/notes-on-soft-actor-critic-off-policy-maximum-entropy-deep-reinforcement-learning-with-a-stochastic-actor/

[10] https://math.stackexchange.com/questions/930931/explanation-of-how-probability-density-functions-transform-under-the-change-of-v

[11] https://en.wikipedia.org/wiki/Probability_density_function#Function_of_random_variables_and_change_of_variables_in_the_probability_density_function