Causal Inference 102

In my blog, I have covered several pieces of information about causal inference:

Causal Inference: we talked about (a) two-stage regression for estimating the causal effect between X and Y even when there is a confounder between them; (b) causal invariant prediction
Tools needed to build an RL debugging tool: we talked about 3 main methods for causal relationship discovery – (a) noise model; (b) quantile regression with the idea of Kolmogorov complexity; (c) matching
Causal Inference in Recommendation Systems: we talked about backdoor/frontdoor adjustment and causal relationship discovery in a sequence modeling setting

This time, I read a paper about learning causal relationship from pure observational data [1]. It has a very clear introduction of causal inference, which inspires me to write another introduction post of causal inference.

Let’s start from basic definitions. Structural causal models (SCM), structural equation models (SEM), or functional causal models (FCM) all refer to the same thing: a graph which indicates causal relationships between nodes and causal relationships are encoded by functions and noises. [1] uses the notation of FCM primarily. Here is an example of an FCM:

collider definition [5]: if a node has two edges pointing to it, it is called a collider. In the example above, x5 is a collider. X3, X4, and X5 form the so-called “v-structure”.

d-separation definition: d-separation is used to determine if a node set X is independent of a node set Y, given a node set Z. Specifically, if X and Y are d-connected, then X and Y are dependent given Z, denoted as $X \not\!\perp\!\!\!\perp_G Y | Z$ ; if X and Y are d-separated, then X and Y are independent given Z, denoted as $X \perp\!\!\!\perp_G Y | Z$ . If two nodes are not d-connected, then they are d-separated. There are several rules for determining whether two nodes are d-connected or d-separated [3]. An interesting (and often non-intuitive) example is that in a v-structure like (X3, X4, X5) above: X3 is d-connected (i.e., dependent) to X4 given X5 (i.e., the collider), even though X3 and X4 has no direct edge in between [4].

Identifiability definition: An observational distribution of all variables could be resulted by different FCMs. Thus, we are not guaranteed to infer the correct causal relationship from observational data. That’s why FCM is a richer structure than pure observational data and using pure probabilistic distributions are not enough to do causal inference! Proposition 4.1 (non-uniqueness of graph structures) in [6] says that there will always be some graph structure to explain an observational data of two variables thus we can never determine the correct causal relationship without additional assumption. If, with correct assumptions, we can identify the ground truth FCM from observational data, we call the FCM is identifiable.

Faithfulness definition: We are given observational data and a hypothesized FCM. Running conditional independence tests on the observational distribution will give us all conditional independence relationships. If all the identified conditional independence relationships from the data are also entailed by the FCM, then the observational distribution is faithful to the FCM. Here is an example [7] that an observational distribution is unfaithful to an FCM:

In the FCM, we can see that A and D are d-connected, meaning A and D are dependent (given an empty set Z).
If A, B, C, and D have the linear relationships indicated as on the right, then 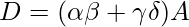$D=(\alpha\beta + \gamma\delta)A$ . When 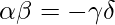$\alpha\beta =- \gamma\delta$ , the conditional independence test will return us 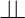$\perp\!\!\!\perp$ . Therefore, the identified conditional independence relationship from the data is not entailed by the FCM.

In practice, inferring FCMs from observational data are based on the Causal Sufficiency Assumption (CSA), Causal Markov Assumption (CMA), and Causal Faithfulness Assumption (CFA) (more details in [1]). Based on these assumptions, inferring FCMs from observational data limits the space of plausible FCMs and involves the following steps:

Determine all possible causal relationships using conditional independent tests and derive the Completed Partially Directed Acyclic Graph (CPDAG)
For undeterminable causal relationships, use constraint-based methods, score-based methods, or hybrid methods to get the best hypothesis

Recall that based on non-uniqueness of graph structures, there will always be some graph structure to explain an observational data of two variables thus we can never determine the correct causal relationship without additional assumption. Now let’s look at what additional assumption we could have to facilitate causal discovery in real world:

LinGAM assumes a linear structure FCM with all variables are continuous:
$X_i = \sum\limits_k \alpha_k P_a^k(X_i)+E_i, \;\; i \in [1, N]$
The LinGAM paper proves that when all probability distributions of source nodes in the causal graph are non-Gaussian, FCM is fully identifiable.
The additive noise model (ANM) assumes that we can learn the true causal direction between X and Y when:
1. $Y=f(X)+E$
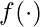2. $f(\cdot)$ is not a linear model with Gaussian input and Gaussian noise
3. Only two variables are involved in the FCM (hence ANM is a bivariate method)
The causal additive model (CAM) is the counterpart of ANM when there are more than 2 variables. Its assumption is similar to ANM that 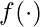$f(\cdot)$ cannot be a linear model with Gaussian input and Gaussian noise for the FCM to be identifiable. (I am not totally sure about CAM’s assumption. We may need to verify more carefully.)

Up to this point, we have finished the causal inference 102 introduction. The proposed method itself in [1] is interesting and useful to me because I need to conduct causal relationship discovery on observational data very often. And its neural network-based method seems general to handle practical data. There are many other causal relationship discovery methods. You can find more in an open source toolbox: [2]

References

[1] Learning Functional Causal Models with Generative Neural Networks: https://arxiv.org/abs/1709.05321

[2] https://fentechsolutions.github.io/CausalDiscoveryToolbox/html/causality.html

[3] https://yuyangyy.medium.com/understand-d-separation-471f9aada503

[4] https://stats.stackexchange.com/a/399010/80635

[5] https://en.wikipedia.org/wiki/Collider_(statistics)

[6] Elements of Causal Inference: https://library.oapen.org/bitstream/handle/20.500.12657/26040/11283.pdf?sequence=1&isAllowed=y

[7] https://www.youtube.com/watch?v=1_b7jgupoAE