It has been some time since I got touch in neural architecture search (NAS) in my PhD, when I tried to get ideas for solving a combinatorial optimization problem for collectible card games’ deck recommendation. My memory about NAS mainly stays in one of the most classic NAS paper “Neural architecture search with reinforcement learning” [1], which uses policy gradient to search for better architectures. Apparently, things have advanced rapidly.
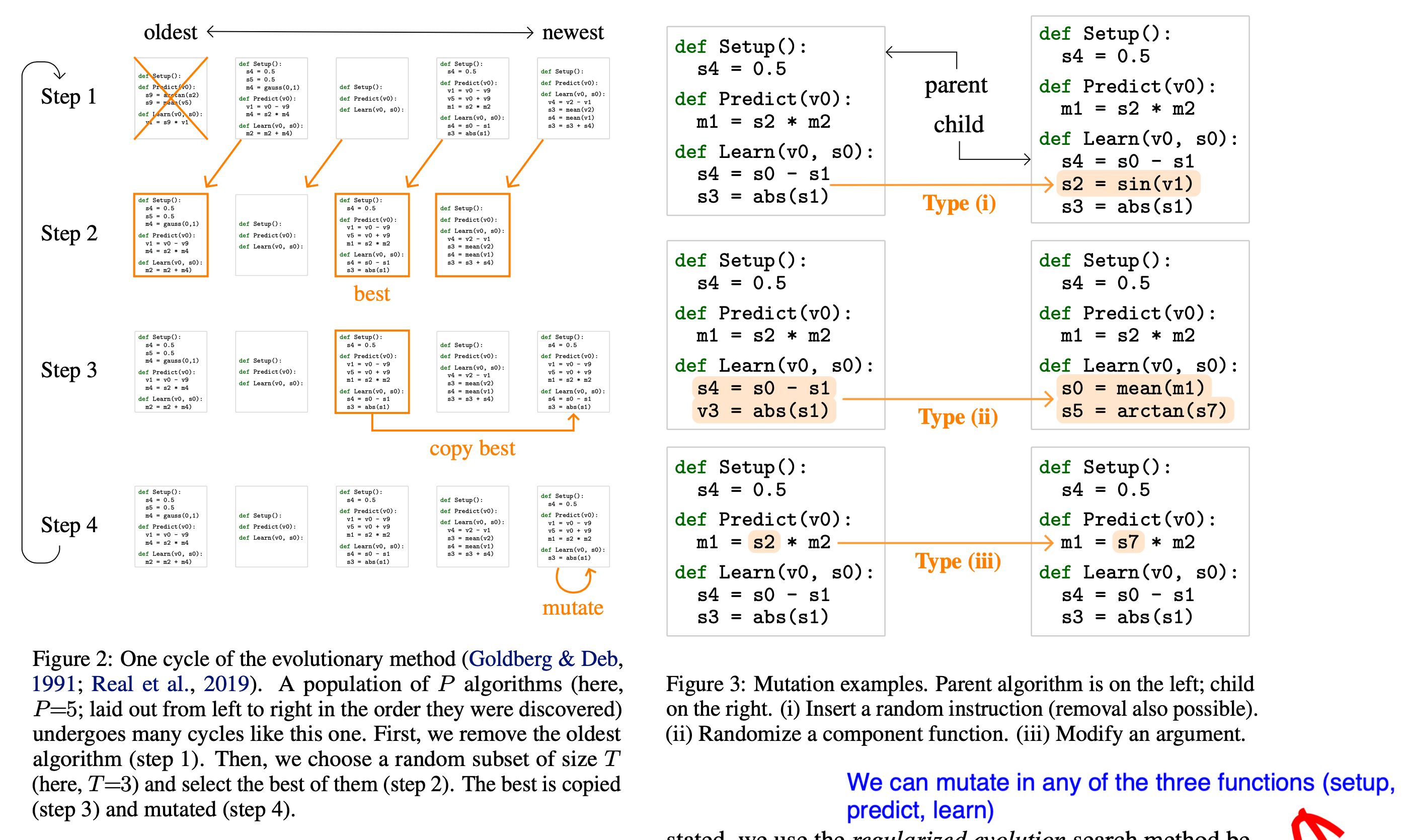
We can start from the most powerful NAS variant, AutoML-Zero [2]. It is not simply evolving an architecture, but actually evolve programs, literally. A program is defined with three main functions, setup(), learn(), and predict(). The algorithm uses evolutionary algorithms to search all possible implementations of the three functions using elementary operations. The objective of evolutionary algorithms is Evaluate() function shown below:

The evolutionary process is best illustrated in the following diagram:
After seeing one of the most advanced NAS development, we can look at simpler ones. EfficientNet shows that deep neural networks can improve the most performance when depth, width, and resolution are scaled up simultaneously. This is a million-dollar-worth finding! Hence, they propose compound scaling, where they simply search over one dimension ![]() :
:

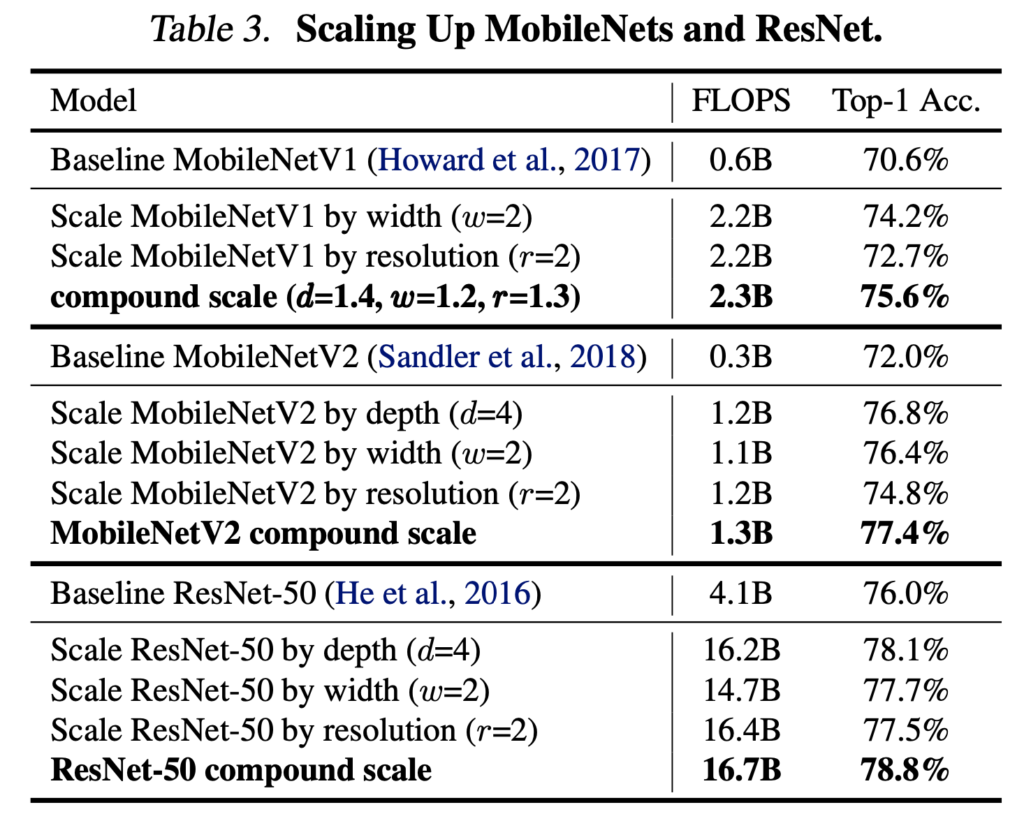
They show that scaling existing models like MobileNet and ResNet up lead to better performance then scaling one dimension (width, depth, resolution).
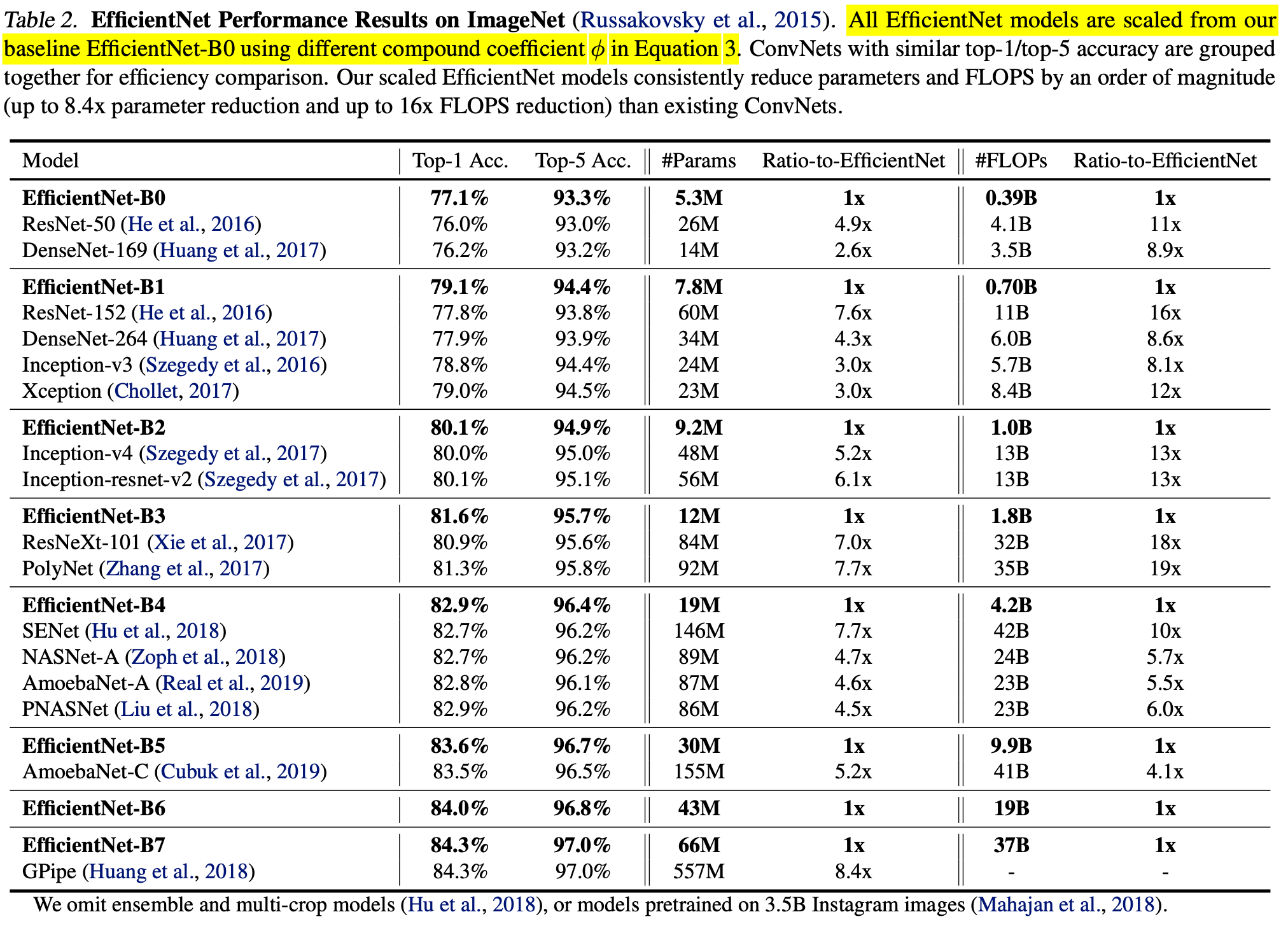
Next, they scale up a baseline model EfficientNet-B0, a model found by MnasNet [4]. As we can see, scaling up MnasNet leads to steady improvement in performance. MnasNet is also a policy gradient-based NAS algorithm, similar to earlier works like [1] (which might not be sample efficient). But it has two main improvements: (1) the reward adds latency penalty; (2) each block is repeating one sub-architectures and different blocks could have different sub-architectures; as comparison, previous works repeat only one sub-architectures in multiple blocks.
Besides EfficientNet, another simple yet effective method is using random search over a predictor that is trained on different possible architectures for predicting their performance (Neural Predictor from [5]). The predictor itself uses graph neural networks (specifically, graph convolutional network) to consume neural architectures represented as graphs. Most graph neural networks learn to represent node embeddings. However, in this work, they are interested in a regression model which maps the overall graph structure (architecture) to a scalar (performance), so they average the node embeddings to represent the overall graph’s embedding as the regression model’s input.
The ancestor of Neural Predictor is PNAS [9], which progressively expands architectures. At each step of expansion, it queries a trained predictor for which block to expand. The predictor is trained on (architecture of ![]() blocks, performance), while it is used to predict the performance of architectures of
blocks, performance), while it is used to predict the performance of architectures of ![]() blocks. PNAS cannot be fully parallelizable because of its progressive nature. That is one downside compared to Neural Predictor.
blocks. PNAS cannot be fully parallelizable because of its progressive nature. That is one downside compared to Neural Predictor.
Now, let’s move on to one-shot NAS, which mostly revolve around the weight sharing technique. We use One-Shot [10], DARTS [11], and ProxylessNAS [8] to introduce the weight sharing technique. Weight sharing uses a much bigger architecture for training a model. The larger architecture covers all possible architectures we want to consider. If there are ![]() possible architectures
possible architectures ![]() , then the output of One-Shot net and DARTS is (as summarized in ProxylessNAS [8]):
, then the output of One-Shot net and DARTS is (as summarized in ProxylessNAS [8]):
 , where
, where ![]() in
in ![]() is a softmax distribution over the
is a softmax distribution over the ![]() architectures. To be clear, from the equation above, in order to compute
architectures. To be clear, from the equation above, in order to compute ![]() or
or ![]() , we have to compute all the
, we have to compute all the ![]() architectures’ outputs.
architectures’ outputs.
The problem with One-Shot and DARTS is that the memory needs to hold all ![]() architectures hence may easily blow up. ProxylessNAS proposes a technique called BinaryConnect, which is very close to DARTS but has subtle difference. BinaryConnect means that
architectures hence may easily blow up. ProxylessNAS proposes a technique called BinaryConnect, which is very close to DARTS but has subtle difference. BinaryConnect means that ![]() , where
, where ![]() is sampled from a softmax distribution. The difference with DARTS is that
is sampled from a softmax distribution. The difference with DARTS is that ![]() is strictly one architecture’s output, rather than a weighted sum of
is strictly one architecture’s output, rather than a weighted sum of ![]() architectures. To take gradients of
architectures. To take gradients of ![]() , they propose a trick to sample two architectures every time when computing the gradient:
, they propose a trick to sample two architectures every time when computing the gradient:


ProxylessNAS also proposes to train a neural network to predict latency so that model prediction accuracy and latency can be both differentiable w.r.t. architectures.
ENAS [12] is actually the originator of the weight sharing technique. One hurdle ENAS has over ProxylessNAS is that it requires an additional RNN controller to decide which architecture to sample. ProxylessNAS only needs to learn the softmax distribution parameters ![]() .
.
TuNAS [6] can be seen as an improved version over ProxylessNAS. There are mainly two improvements:
(1) more aggressive weight sharing, which they called operation collapsing. 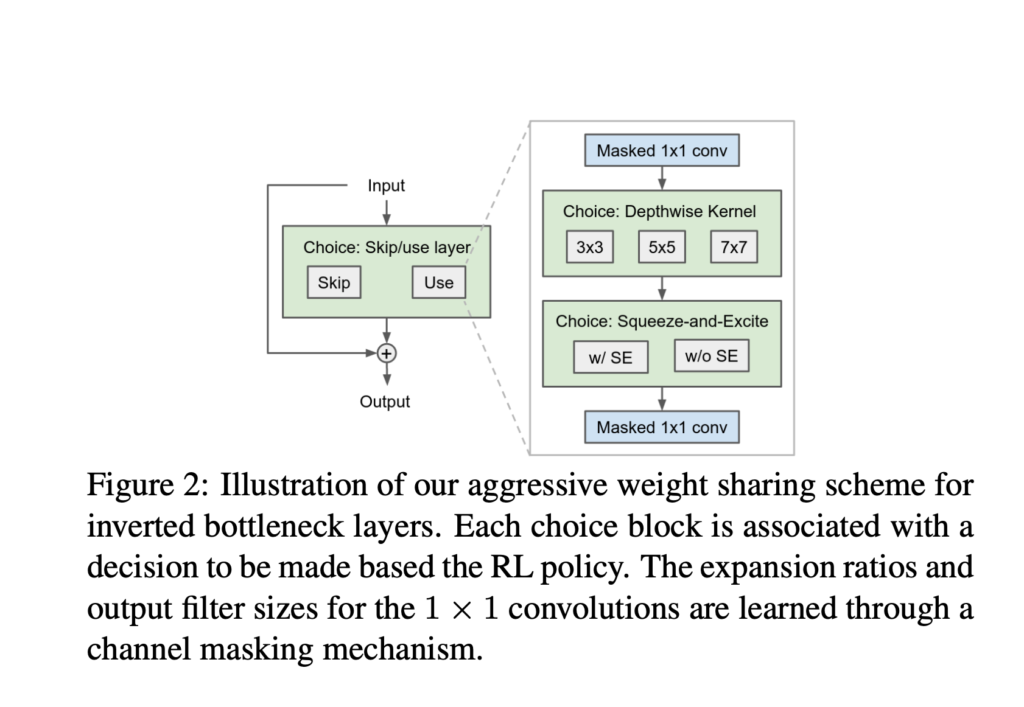

(2) a new reward function, which they claim leads to more robust results:

In TuNAS, policy gradient is used for sampling potential architectures, while weight sharing updates the sampled architectures’ weights. As the RL policy samples more and more architectures which cover all possible weights, all the weights in the biggest architecture get learned well. The overall learning loop is described as:

However, one problem arises from the weight sharing technique, as pointed out in the abstract of the BigNAS paper [7]: “existing methods assume that the weights must be retrained, fine-tuned, or otherwise post-processed after the search is completed”. BigNAS proposes several empirical tricks to make sure that architectures found by weight sharing can achieve good performance without retraining or post-processing steps. First, they introduce the sandwich rule, which samples the smallest child model, the biggest full model, and N randomly sampled child models. The gradients are aggregated from all the sampled models before relevant weights get updated. As [7] hypothesized, “The motivation is to improve all child models in our search space simultaneously, by pushing up both the performance lower bound (the smallest child model) and the performance upper bound (the biggest child model) across all child models.” Second, they introduce inplace distillation, which means the biggest full model’s prediction is used to supervise all child models through the whole training process. I am actually not sure why using the ground-truth labels for child models would be inferior than the teacher network’s prediction. Third, they design a learning rate schedule while ends up at a constant rather than simply exponentially decreasing. Moreover, they dedicate section 3.2 to describe a coarse-to-fine architecture selection paradigm after the full model is trained.
In parallel, few-shot NAS tries to solve a similar problem that evaluation based on the subnets sampled from a one-shot supernet usually have imperfect correlation with the evaluation based on those subnets retrained from scratch. So in few-shot NAS, multiple supernets are trained so that sampled subnets have better evaluation correlation. With less weight sharing than one-shot NAS but still lower computation than not using weight sharing, few-shot strikes a good balance. Please check [13] for more details.
In the last, I want to spend some time to specifically walk through some details from DARTS [11], SNAS [14], and DSNAS [15], which involves several advanced gradient-based methods to do one-shot learning.
In DARTS, as we survey when we introduce ProxylessNAS, the outcome of an input ![]() is a softmax distribution over a set of candidate operators
is a softmax distribution over a set of candidate operators ![]() :
: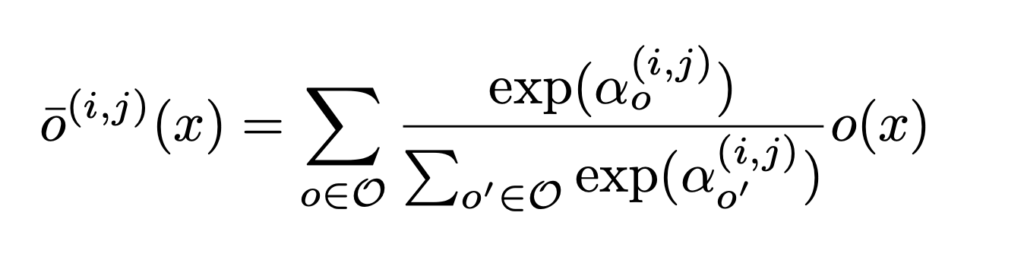
![]() then is a learnable vector determining which operator to be more preferable. Suppose the network’s own weight is
then is a learnable vector determining which operator to be more preferable. Suppose the network’s own weight is ![]() , then the objective function of DARTS is essentially:
, then the objective function of DARTS is essentially: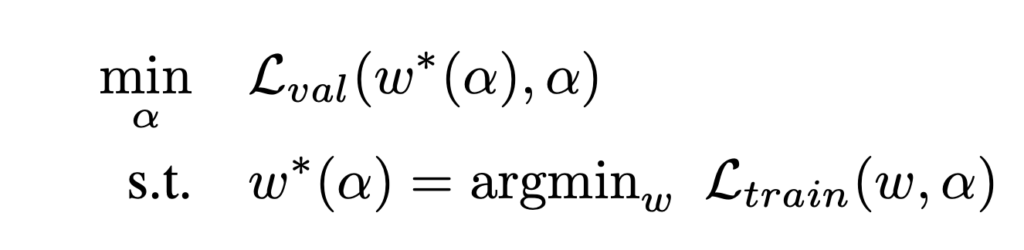 Note that
Note that ![]() is actually optimized on the validation dataset. As the paper suggests, this is a bi-level optimization problem. Analytically, the optimal solution is obtained when
is actually optimized on the validation dataset. As the paper suggests, this is a bi-level optimization problem. Analytically, the optimal solution is obtained when ![]() and
and ![]() .
.
The paper proposes to replace ![]() , the expensive minimization
, the expensive minimization ![]() , with
, with ![]() .
.
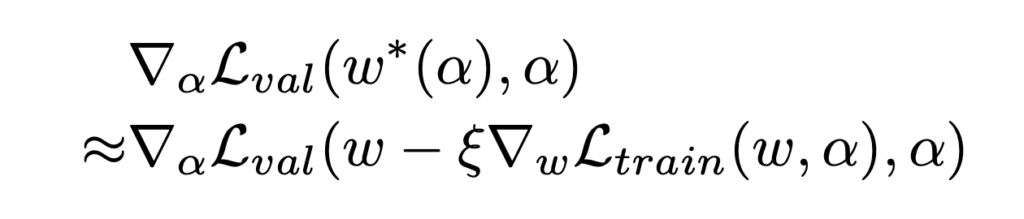
However, now ![]() and
and ![]() , the first and second argument in
, the first and second argument in ![]() , are both a function of
, are both a function of ![]() , so we need to use the derivative rule of multi-variable functions to really compute
, so we need to use the derivative rule of multi-variable functions to really compute ![]() . I refer to https://math.libretexts.org/Bookshelves/Calculus/Book%3A_Calculus_(OpenStax)/14%3A_Differentiation_of_Functions_of_Several_Variables/14.5%3A_The_Chain_Rule_for_Multivariable_Functions and https://www.programmersought.com/article/14295360685/#67_176 to really understand how to compute
. I refer to https://math.libretexts.org/Bookshelves/Calculus/Book%3A_Calculus_(OpenStax)/14%3A_Differentiation_of_Functions_of_Several_Variables/14.5%3A_The_Chain_Rule_for_Multivariable_Functions and https://www.programmersought.com/article/14295360685/#67_176 to really understand how to compute ![]() .
.
We use a simpler notation to represent ![]() , where
, where ![]() ,
, ![]() ,
, ![]() .
.
From the derivative rule of multi-variable functions
we have:
![]()
So we finally compute ![]() as:
as:
![]()
As you may notice, ![]() is an expensive matrix-vector product, so people propose to use the finite difference approximation:
is an expensive matrix-vector product, so people propose to use the finite difference approximation:
![]()
where ![]()
The finite difference approximation is actually based on Taylor expansion:
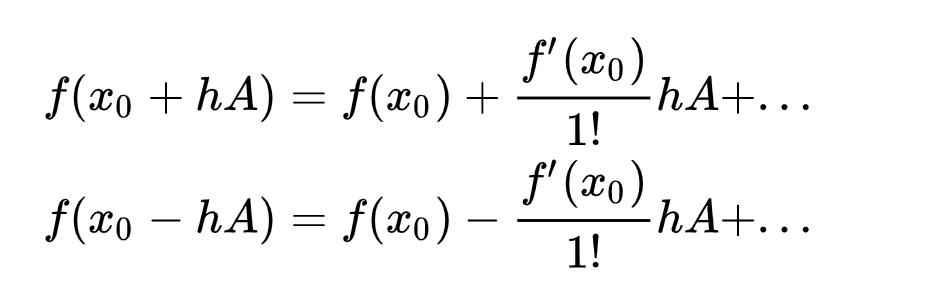
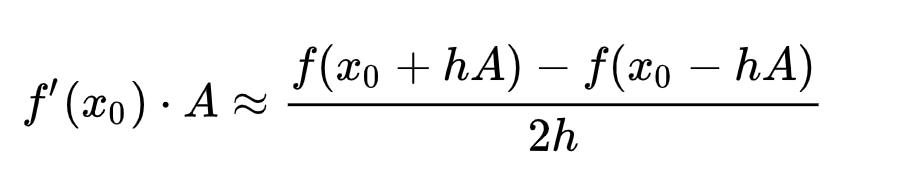
The problem with DARTS is that after learning both the architecture selection parameter ![]() and the supernet’s own weight
and the supernet’s own weight ![]() , it derives the best child network by
, it derives the best child network by ![]() . As pointed out by SNAS [14], DARTS thus has “the inconsistency between the performance of derived child networks and converged parent networks”. SNAS uses the concrete distribution as the more principled way to learn the architecture selection parameter
. As pointed out by SNAS [14], DARTS thus has “the inconsistency between the performance of derived child networks and converged parent networks”. SNAS uses the concrete distribution as the more principled way to learn the architecture selection parameter ![]() . In the concrete distribution, there is a parameter
. In the concrete distribution, there is a parameter ![]() that will be annealed to be close to zero thus when the training finished, the architecture selection parameter will converge to discrete variables (clearly denoting which operator is connected between which pair of nodes).
that will be annealed to be close to zero thus when the training finished, the architecture selection parameter will converge to discrete variables (clearly denoting which operator is connected between which pair of nodes).
The notations in the SNAS paper [14] is a bit chaotic. Hope I can comb them more cleanly. The idea of SNAS is that the architecture search parameter is a binary tensor ![]() .
. ![]() denotes the node
denotes the node ![]() is connected to node
is connected to node ![]() with operator
with operator ![]() . Therefore,
. Therefore, ![]() is actually a one-hot encoding vector of length
is actually a one-hot encoding vector of length ![]() , i.e., the selection of one of the
, i.e., the selection of one of the ![]() possible operators connecting node
possible operators connecting node ![]() and
and ![]() . Similarly,
. Similarly, ![]() is also a vector of length
is also a vector of length ![]() , denoting the output of the
, denoting the output of the ![]() possible operators.
possible operators.

Therefore, the objective function of SNAS is:
![]()
where
Now, ![]() will be parameterized by the concrete distribution, which constitutes the parameter selection parameter
will be parameterized by the concrete distribution, which constitutes the parameter selection parameter ![]() of the same size of
of the same size of ![]() , i.e.,
, i.e., ![]() , the Gumbel random variable
, the Gumbel random variable ![]() , and the annealing parameter
, and the annealing parameter ![]() . Specifically,
. Specifically,
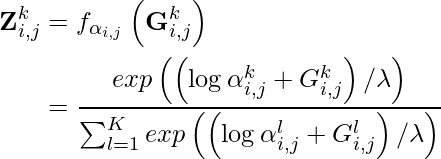
The authors proves that ![Rendered by QuickLaTeX.com \mathbb{E}_{\mathbf{Z} \sim p_\alpha(\mathbf{Z})}\left[\frac{\partial \mathcal{L}_\theta(\mathbf{Z})}{\partial \alpha_{i,j}^k}\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9bc7133456ea15e95381b11e354287d0_l3.png) is essentially doing policy gradient.
is essentially doing policy gradient.
First, we make sure we are clear on the notations on how node ![]() ‘s input
‘s input ![]() interacts with other nodes that connect to it (small modification from equation 20 in [14]):
interacts with other nodes that connect to it (small modification from equation 20 in [14]):
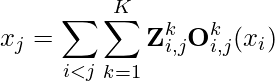
Now, using the chain rule of derivatives, we have
![Rendered by QuickLaTeX.com \begin{align*}\begin{split}\frac{\partial \mathcal{L}_\theta(\mathbf{Z})}{\partial \alpha_{i,j}^k} &=\sum_{k'=1}^{K} \frac{\partial \mathcal{L}_\theta(\mathbf{Z})}{\partial x_j} \cdot \frac{\partial x_j}{\partial \mathbf{Z}_{i,j}^{k'}} \cdot \frac{\partial \mathbf{Z}_{i,j}^{k'}}{\partial \alpha_{i,j}^k} \\&=\sum_{k'=1}^{K} \frac{\partial \mathcal{L}_\theta(\mathbf{Z})}{\partial x_j} \cdot \mathbf{O}_{i,j}^{k'}(x_i) \cdot \frac{\partial \mathbf{Z}_{i,j}^{k'}}{\partial \alpha_{i,j}^k} \qquad\qquad (\text{replace } \frac{\partial x_j}{\partial \mathbf{Z}_{i,j}^{k'}}) \\&=\sum_{k'=1}^{K} \frac{\partial \mathcal{L}_\theta(\mathbf{Z})}{\partial x_j} \cdot \mathbf{O}_{i,j}^{k'}(x_i) \cdot \left(\left(\delta(k'-k)-\mathbf{Z}_{i,j}^{k'}\right)\mathbf{Z}_{i,j}^{k'}\frac{1}{\lambda \alpha_{i,j}^k}\right) \qquad(\text{replace } \frac{\partial x_j}{\partial \mathbf{Z}_{i,j}^{k'}}\text{ based on trick [16]})\end{split}\end{align*}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9dab0d80fcafe83d0428f24f6ed7206e_l3.png)
Finally, Appendix D shows that:
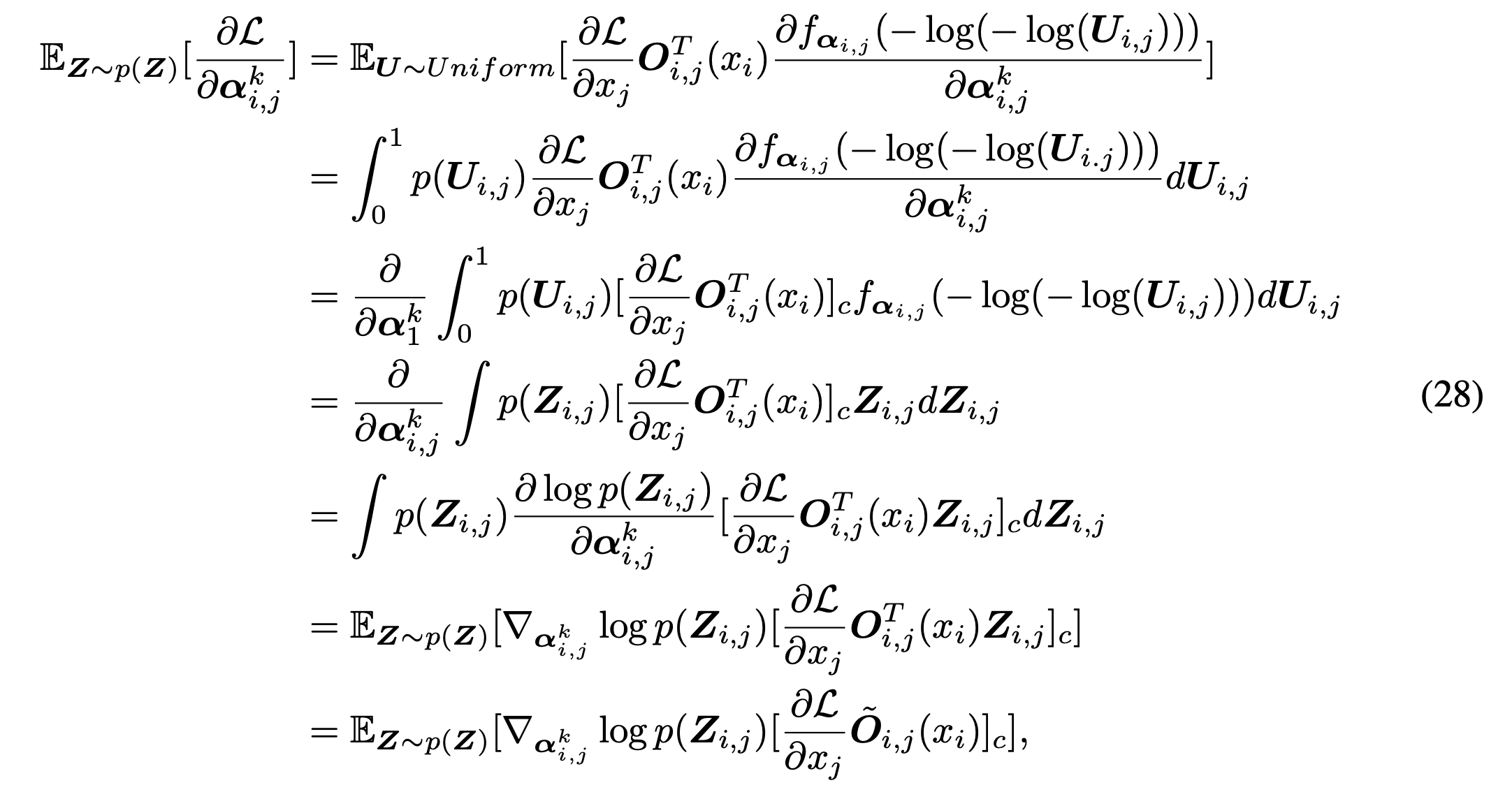
That’s the form of policy gradient. That’s why it is equivalent to say that SNAS is trained with policy gradient and with reward ![]() .
.
I’ll dig into DSNAS [15] once it gets more attention.
——————– Update 2021/09 ——————–
I want to mention two more classic ideas of NAS.
- Regularized evolution [17], in which every mutated solution has a certain survival period. The only way that a good architecture can remain the population is by being passed down from parents to children through the generations. “regularized” means every solution has an age, therefore it encourages more diversity and exploration and avoids being stuck by spuriously promising solutions.
- Bayesian Optimization [18], in which there are five most important components: encoding, neural predictor, uncertainty estimate, acquisition function, and acquisition optimization. [18] used empirical experiments to find the optimal combination of them: path encoding (a specific feature engineering method they propose), an ensemble of 5 feedforward neural networks as uncertainty estimate, independent Thompson Sampling, and mutation-based acquisition optimization.
References (arxiv submitted time)
[1] NEURAL ARCHITECTURE SEARCH WITH REINFORCEMENT LEARNING (2016.11)
[2] AutoML-Zero: Evolving Machine Learning Algorithms From Scratch (2020.3)
[3] EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (2019.5)
[4] MnasNet: Platform-aware neural architecture search for mobile (2018.7)
[5] Neural Predictor for Neural Architecture Search (2019.12)
[6] Can weight sharing outperform random architecture search? An investigation with TuNAS (2020.8)
[7] BigNAS: Scaling Up Neural Architecture Search with Big Single-Stage Models (2020.3)
[8] ProxylessNAS: Direct Neural Architecture Search on Target Task and Hardware (2018.12)
[9] Progressive Neural Architecture Search (2017.12)
[10] Understanding and Simplifying One-Shot Architecture Search (2018)
[11] DARTS: Differentiable Architecture Search (2018. 6)
[12] Efficient Neural Architecture Search via Parameter Sharing (2018.2)
[13] Few-shot Neural Architecture Search (2020.6)
[14] SNAS: Stochastic Neural Architecture Search (2018.12)
[15] DSNAS: Direct Neural Architecture Search without Parameter Retraining (2020.2)
[16] softmax derivative trick https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/
[17] Regularized Evolution for Image Classier Architecture Search (2019.2)
[18] BANANAS: Bayesian Optimization with Neural Architectures for Neural Architecture Search (2020.11)