You are given an m x n binary matrix grid. An island is a group of 1‘s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1:
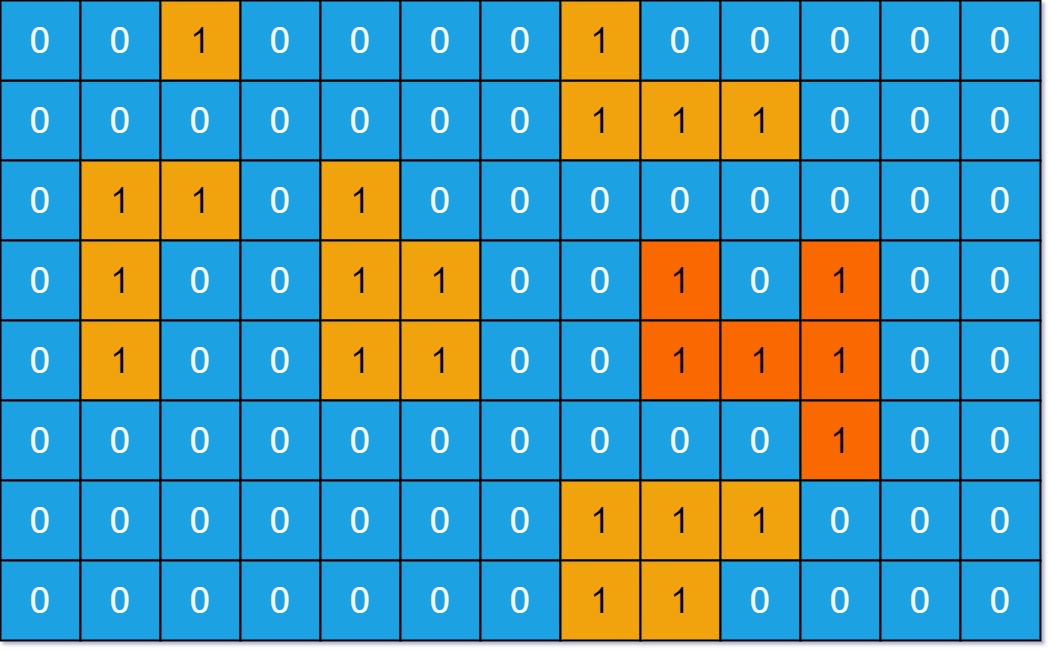
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0or1.
BFS/DFS
Ideas
Traverse the grid. For every cell with value 1, you can use DFS or BFS to further traverse its neighbors and count the number of nodes visited as the value of the connected area. At the end of the traversal, you can just take the maximum of all the areas associated to each value-1 cell.
class Solution(object):
def maxAreaOfIsland(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
height, width = len(grid), len(grid[0])
def dfs(i, j):
if i < 0 or i >= height or j < 0 or j >= width:
return 0
if grid[i][j] == 1:
grid[i][j] = 0
return 1 + dfs(i-1, j) + dfs(i+1, j) + dfs(i, j-1) + dfs(i, j+1)
else:
return 0
def bfs(i, j):
if grid[i][j] == 0:
return 0
grid[i][j] = 0
nodes = [(i, j)]
area = 0
while nodes:
x, y = nodes.pop(0)
area += 1
for dx, dy in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
x_, y_ = x + dx, y + dy
if x_ < 0 or x_ >= height or y_ < 0 or y_ >= width:
continue
if grid[x_][y_] == 1:
grid[x_][y_] = 0
nodes.append((x_, y_))
return area
max_area = 0
for x in range(height):
for y in range(width):
# area = dfs(x,y)
area = bfs(x, y)
max_area = max(area, max_area)
return max_area
Union Find
I think the clearest online reference is from this post:
https://leetcode.com/problems/max-area-of-island/discuss/729303/Python-BFS-and-Union-Find
Idea:
Union find is an algorithm in which we maintain each node’s parent as an array. The node parent is initialized such that each node’s parent is itself. While we traverse nodes, we will iteratively update the node parent array until connected nodes’ parents converge to the same node. We also maintain a size array, which keeps the record of the size of connected nodes. We have used union find for other leetcode problems. One good and succinct example is https://czxttkl.com/2015/10/19/leetcode-261-graph-valid-tree/.
class Solution(object):
def maxAreaOfIsland(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
height, width = len(grid), len(grid[0])
# initialization for union find
size = [[0 for j in range(width)] for i in range(height)]
parent = [[(None, None) for j in range(width)] for i in range(height)]
for i in range(height):
for j in range(width):
parent[i][j] = (i, j)
if grid[i][j] == 1:
size[i][j] = 1
def union_find(p, q):
if parent[p][q] == (p, q):
return p, q
else:
return union_find(*parent[p][q])
for i in range(height):
for j in range(width):
if grid[i][j] == 1:
for next_i, next_j in ((i, j+1), (i+1, j)):
if next_j >= width:
continue
if next_i >= height:
continue
if grid[next_i][next_j] != 1:
continue
parent_ij = union_find(i, j)
parent_ij1 = union_find(next_i, next_j)
if parent_ij == parent_ij1:
continue
x, y = parent_ij[0], parent_ij[1]
w, z = parent_ij1[0], parent_ij1[1]
if size[x][y] < size[w][z]:
parent[x][y] = parent[w][z]
size[w][z] += size[x][y]
else:
parent[w][z] = parent[x][y]
size[x][y] += size[w][z]
max_area = 0
for i in range(height):
for j in range(width):
max_area = max(max_area, size[i][j])
return max_area