Information Bottleneck + RL Exploration

In this post, we are going to discuss one good idea from 2017 – information bottleneck [2]. Then we will discuss how the idea can be applied in meta-RL exploration [1].

Mutual Information

We will start warming up by revisiting a classic concept in information theory, mutual information [3]. Mutual information $I(X;Y)$ measures the amount of information obtained about one random variable by observing the other random variable:
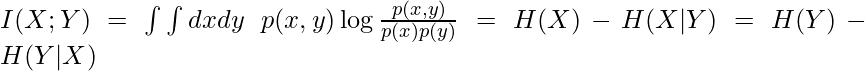$I(X;Y) = \int\int dx dy \; p(x,y)\log\frac{p(x,y)}{p(x)p(y)} = H(X) - H(X|Y) = H(Y)-H(Y|X)$ . From [3], we can see how these equations are derived:

Stochastic Variational Inference and VAE

Stochastic variational inference (SVI) is a useful technique to approximate intractable posterior distribution. One good example is to use SVI for VAE. We have introduced SVI [4] and VAE [5] separately. In this post, we are going to explain both concepts again unifying the two concepts. A stackexchange post [7] also helped shape my writing.

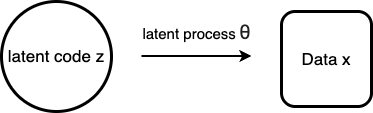
Suppose we have data $x$ and hypothesize data is generated by a latent process $\theta$ , starting from a latent code $z$ .

Then what we want to do is to maximize $\log p_\theta(x)$ , sometimes called the “log evidence”. Let $p_\theta(z|x)$ to describe the posterior probability of $z$ given observing $x$ and $p_\theta(x,z)$ to describe the joint probability of $x$ and $z$ . Note that, $p_\theta(z|x)$ is infeasible to compute in general. Therefore, we introduce $q_\phi(z|x)$ to approximate $p_\theta(z|x)$ , with $\phi$ being learnable parameters. $q_\phi(z|x)$ is tractable, for example, a neural network with outputs representing a Gaussian distribution’s mean and variance but can only approximate the true posterior distribution, $p_\theta(z|x)$ . It turns out that $log p_\theta(x)$ can be rewritten into [see 6, page 22-23 for derivation]:
$log p_\theta = KL\left(q_\phi(z|x) \Vert p_\theta(z|x)\right) - KL\left(q_\phi(z|x) \Vert p_\theta(x, z) \right)$ .

We call the second term, $- KL\left(q_\phi(z|x) \Vert p_\theta(x, z)\right)$ , the evidence lower bound (ELBO). We have $log p_\theta \geq - KL\left(q_\phi(z|x) \Vert p_\theta(x, z)\right) = ELBO$ because $KL\left(q_\phi(z|x) \Vert p_\theta(z|x)\right) \geq 0$ . Therefore, we can maximize ELBO w.r.t. $\phi$ in order to maximize $log p_\theta(x)$ .

ELBO can be further derived into [see derivation in 5]:
$log p_\theta(x) \geq - KL\left(q_\phi(z|x) \Vert p_\theta(x, z)\right) = \newline \mathbb{E}_{z\sim q_\phi(z|x)}\left[ log p_\theta(x|z)\right] - KL\left( q_\phi(z|x) \Vert p(z) \right)$ ,
where $p(z)$ is the prior for the latent code (e.g., standard normal distributions). In VAE, we also use a deterministic neural network to approximate $log \; p_\theta(x|z) \approx log \; q_{\phi'}(x|z)$ . Overall, $\mathbb{E}_{z\sim q_\phi(z|x)}\left[ log q_{\phi'}(x|z)\right] - KL\left( q_\phi(z|x) \Vert p(z) \right)$ can be learned by minibatch samples and when ELBO is maximized, $q_\phi(z|x)$ infinitely approximates $p_\theta(z|x)$ .

Deep Variational Information Bottleneck

If you view VAE as a clever idea to encode information of $x$ (data) in an unsupervised learning setting, Deep Variational Information Bottleneck [2] is an extended idea to encode latent information from $x$ (data) to $y$ (label) in a supervised learning setting. The objective is to encode $x$ into latent code $z$ with as little mutual information as possible, while making $z$ preserve as much as possible mutual information with $y$ :

After some derivation shown in [2], we can show that we can also instead maximize a lower bound (notations slightly different than [2] because I want it to be consistent in this post):
$I(z;y) - \beta I(z;x) \geq \mathbb{E}_{z\sim q_{\phi}(z|x)}\left[ log q_{\phi'}(y|z) \right]-\beta KL\left(q_\phi(z|x) \Vert p(z)\right),$
where, again, $q_\phi(z|x)$ is the variational distribution to the true posterior distribution $p_\theta(z|x)$ and $q_{\phi'}(y|z)$ is the decoder network.

Meta-RL Exploration By a Deep Variational Information Bottleneck Method

With all necessary ingredients introduced, we now introduce how Meta-RL exploration can benefit from Information Bottleneck [1]. The basic Meta-RL setup is that we have diverse environments. Each environment is represented with a tensor (could be a one-hot encoding) $\mu$ , which is known at training time but unknown at testing time. The authors of [1] propose to learn two policies: $\pi^{exp}_{\phi}(a|s)$ for exploring environments with the goal to collect as much information about the environment as possible, and $\pi^{task}_{\theta}(a|s, z)$ for exploiting an environment with a known encoded tensor $z$ . In training time, $z \sim \mathcal{F}_{\psi}(z|u)$ , an encoder to encode environment tensor $u$ (available in training time) or $z \sim q_\omega(z|\tau^{exp})$ , a variational encoder which converts the trajectory generated by $\pi^{exp}_{\phi}(a|s)$ to an encoded tensor. The variational encoder $q_\omega(z|\tau^{exp})$ will be learned to match $\mathcal{F}_{\psi}(z|u)$ in training time. Once $\theta$ , $\phi$ , $\omega$ , and $\psi$ are learned, at testing time, we can run $\pi^{exp}_{\phi}(a|s)$ to collect trajectories $\tau^{exp}$ , use $q_\omega(z|\tau^{exp})$ to determine the environment’s encoded tensor $z$ , and run $\pi^{task}_{\theta}(a|s, z)$ on top to maximize rewards.

The paper uses the mutual information / deep variational information bottleneck ideas in two places. First, when we learn $\pi^{task}_{\theta}(a|s, z)$ and $\mathcal{F}_{\psi}(z|u)$ , we use the following loss function to encourage $z$ encoding minimal information from $\mu$ :
$\text{minimize} \qquad I(z;u) \newline \text{subject to} \quad \mathbb{E}_{z \sim F_{\psi}(z|\mu)}\left[ V^{\pi_\theta^{task}}(z;\mu)\right]=V^*(\mu) \text{ for all } \mu$

The constrained optimization loss function can be converted to a unconstrained loss function by the lagrangian method, with $\lambda$ set as a hyperparameter [8]:
$\text{maximize}_{\psi, \theta}\quad \mathbb{E}_{\mu \sim p(\mu), z\sim F_{\psi}(z|\mu)}\left[V^{\pi_\theta^{task}}(z;\mu) \right] - \lambda I(z;\mu)$

Using the same derivation from [2] (Eqn. 13 & 14), we know the lower bound of $-I(z;u)$ is $-KL(F_{\psi}(z|\mu)\Vert p(z))$ , which has an analytic form when the prior $p(z)$ is chosen properly (e.g., Gaussian). Thus the unconstrained loss function can be maximized on a lower bound.

Second, we encourage to maximize the mutual information between the trajectories explored by $\pi^{exp}_{\phi}(a|s)$ and $z \sim F_{\psi}(z|\mu)$ :
$I(\tau^{exp};z) = H(z) - H(z|\tau^{exp}) \geq H(z) + \mathbb{E}_{\mu, z\sim F_\psi, \tau^{exp}\sim \pi^{exp}}\left[ q_\omega(z|\tau^{exp}) \right]$
(The inequality uses the fact that the KL divergence between the true posterior distribution and the variational distribution, $KL(p(z|\tau^{exp}) \Vert q_\omega(z|\tau^{exp}))$ , is greater than or equal to 0. )

As we see in the paper, $q_\omega$ is learned to match $\mathcal{F}_{\psi}(z|u)$ , while, with some trick to rearrange $\mathbb{E}_{\mu, z\sim F_\psi, \tau^{exp}\sim \pi^{exp}}\left[ q_\omega(z|\tau^{exp}) \right]$ , we can optimize $\pi^{exp}_{\phi}(a|s)$ in an MDP with reward set as information gain of each step.