Some SOTA Model-based RL

Model-based RL has always intrigued me more than model-free RL. Because the former converts RL problems into supervised learning problems which can always employ SOTA deep learning techniques. In this post, I am introducing several latest developments of model-based RL. I categorize them into planning and non planning-based.

Planning

This is one I am reviewing so I am only referencing it with a short name MOPP. The model-based planning algorithm works as follows:

From the paper, this algorithm contains three components: (1) guided trajectory rollout; (2) trajectory pruning; (3) trajectory optimization:

In (1), we first train an ensemble of behavior cloning models 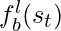$f_b^l(s_t)$ for $l = 1, \cdots, K_2$ . Each behavior cloning model models the output action as a normal distribution with a predicted mean and standard deviation. Each time when we want to sample an action, we first randomly pick a behavior cloning model and then sample the action multiple times according to the predicted mean and standard deviation. However, there is some additional adaptation for how to sample from the predicted mean and standard deviation. First, the standard deviation is scaled larger so that action sampling can be more diverse and aggressive. Second, to counter sampling bad actions, we learn a Q-function from logging data and use it to finally select the action to proceed the trajectory simulation. Although the Q-function estimates the Q-value for the behavior policy instead of the policy being learned, the authors argue that it “provides a conservative but relatively reliable long-term prior information”. The two points are manifested in Eqn. 3: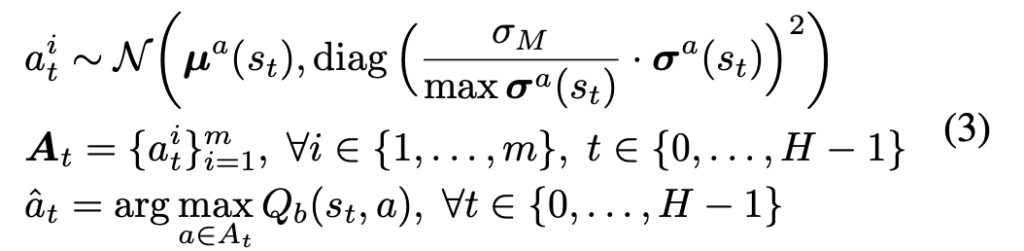
In (2), we use a threshold 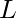to prune trajectories with overall uncertainty larger than that. The way to quantify uncertainty of a trajectory is to look at the sum of each step’s uncertainty defined as 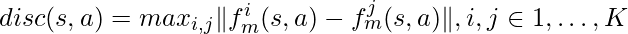, the largest disagreement between any two dynamic models in the ensemble.
- In (3), the final action to perform after planning is some weighted action. The weights come from accumulated predicted returns from the remaining trajectories after pruning in (2):
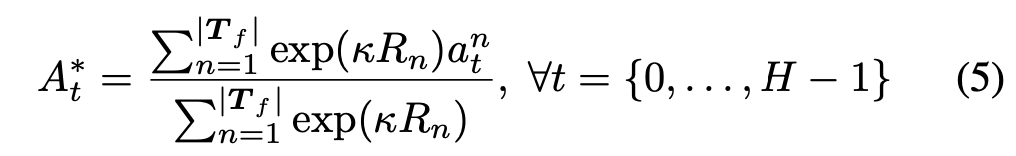  Note one detail at line 14: if we simulate 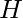$H$ steps, we can get 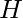$H$ predicted rewards. However, we won’t know what is accumulated return after 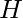$H$ steps. So we would use the learned Q-function and the behavior cloning model to estimate the value after the 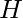$H$ steps.

The MOPP paper has the following comparisons with other existing algorithms. The high-level takeaway is that MOPP is strong when the dataset (medium and med-expert) is less diverse (hence harder for a vanilla supervised learning model to generalize well).

The MOPP paper actually motivates me to review other SOTA model-based methods. As shown in the table, MOPP and MBOP belong to model-based offline planning methods which needs some planning mechanisms, while model-based offline RL methods include MBPO and MOPO which don’t require planning. I’ll introduce MBOP first as another model-based planning algorithm and then move to non-planning based methods.

MBOP [3] is actually a simplified version of MOPP. Compared to MOPP, MBOP lacks:

No value estimate after $H$ -step rollouts
No standard deviation scaling so sampled actions are mostly confined to the behavior policy’s standard deviation.
No uncertainty-based trajectory pruning.

Non-Planning

Non-planning algorithms rely on model-based algorithms in tandem with standard policy optimization methods (like TD3, SAC, etc). One example is called MOPO [1], which adds uncertainty estimate as a penalty to the reward function. Then, they still use model-free algorithms to learn a policy. MOPO works as follows:

As you can see, on line 9, reward function is adjusted by $\lambda max_{i=1}^N \| \Sigma^i (s_j, a_j)\|_F$ , the maximum standard deviation of the learned models in the ensemble. As the authors argue, “empirically the learned variance often captures both aleatoric and epistemic uncertainty, even for learning deterministic functions (where only epistemic uncertainty exists). We use the maximum of the learned variance in the ensemble to be more conservative and robust.”

Another work to use model-based method to adjust the reward function is MORel [4]. It constructs a pessimistic MDP on which standard policy optimization approaches can be applied.