I encountered the noise-contrastive estimation (NCE) technique in several papers recently. So it is a good time to visit this topic. NCE is a commonly used technique under the word2vec umbrella [2]. Previously I talked about several other ways to generate word embeddings in [1] but skipped introducing NCE. In this post, I will introduce it, with notations borrowed from the very paper applying it to word2vec [2].
First, let’s look at an example to get familiar with the NLP terms, target word and context [3], which are denoted as ![]() and
and ![]() in [2]:
in [2]:
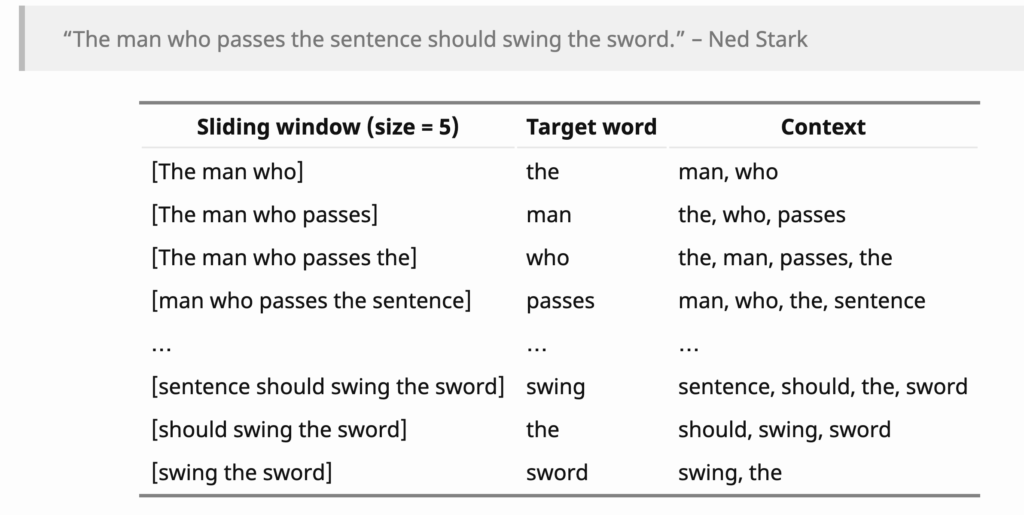
Using the idea of word2vec, words appear together frequently should have similar embeddings. One step further, a word’s embedding should match with the embeddings of its context. Often the context is another embedding derived from the embeddings of the words in the context. For example, the context embedding can be as simple as mean pooling of the embeddings of all the words in the context.
Translating this idea into a loss function, we want to increase the following probability for every observed pair of ![]() :
:
(1) 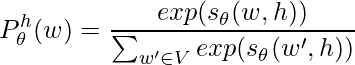
where ![]() is a scoring function to score the similarity of any pair
is a scoring function to score the similarity of any pair ![]() , and
, and ![]() comes from all other possible words in the entire vocabulary. Obviously, this can be an expensive loss function if the vocabulary size is large, which is usually the case.
comes from all other possible words in the entire vocabulary. Obviously, this can be an expensive loss function if the vocabulary size is large, which is usually the case.
To avoid the inefficiency of computing pairwise scores for all the words, NCE proposes to transform the problem of Eqn.1 into a binary classification problem. For an observed pair ![]() , we randomly pick
, we randomly pick ![]() additional words from the vocabulary to form a negative sample set. Among the k+1 words (
additional words from the vocabulary to form a negative sample set. Among the k+1 words (![]() and
and ![]() sampled words), we look at each word
sampled words), we look at each word ![]() and compute the probability that it is from the original observed pair
and compute the probability that it is from the original observed pair ![]() . The fact that
. The fact that ![]() appears as one word in the k+1 words is either due to being sampled from the distribution
appears as one word in the k+1 words is either due to being sampled from the distribution ![]() provided
provided ![]() is from the observed pair
is from the observed pair ![]() , or due to being sampled from a uniform distribution
, or due to being sampled from a uniform distribution ![]() at least one out of
at least one out of ![]() times. Using Bayesian Theorem (more details in [3]), we can actually derive the conditional probability of
times. Using Bayesian Theorem (more details in [3]), we can actually derive the conditional probability of ![]() being from the observed pair given
being from the observed pair given ![]() is already in the
is already in the ![]() words:
words:
(2) 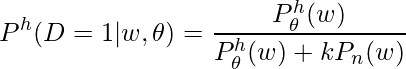
The classification objective then becomes that for the word ![]() from
from ![]() ,
, ![]() should be as high as possible; for the word
should be as high as possible; for the word ![]() from the negative samples,
from the negative samples, ![]() should be as high as possible. That is what Eqn. 8 from [2] is about:
should be as high as possible. That is what Eqn. 8 from [2] is about:
(3) ![]()
There exists some theoretical reasons that I am not too sure about, but which can be taken advantage of to relax the definition of ![]() . That is, we replace
. That is, we replace ![]() in Eqn. 2 with an unnormalized score
in Eqn. 2 with an unnormalized score ![]() . With the replacement, we won’t need to worry about how to compute the partition function
. With the replacement, we won’t need to worry about how to compute the partition function ![]() as in Eqn. 1.
as in Eqn. 1.
There are also variants of NCE loss. One is called InfoNCE (see Eqn. 4 in [4]) and has been applied to model-based reinforcement learning [5]. [4] claims that its objective function is actually optimizing the lower bound on mutual information between ![]() and
and ![]() in the word2vec context (or state and next state in the reinforcement learning context). Mutual information can be understood as the uncertainty reduction of
in the word2vec context (or state and next state in the reinforcement learning context). Mutual information can be understood as the uncertainty reduction of ![]() after observing
after observing ![]() [6].
[6].
References
[1] https://czxttkl.com/2017/01/02/embedding-and-heterogeneous-network-papers/
[2] Learning word embeddings efficiently with noise-contrastive estimation
[4] Representation Learning with Contrastive Predictive Coding