Practical considerations of off-policy policy gradient

I’d like to talk more about policy gradient [1], which I touched upon in 2017. In common online tutorials, policy gradient theorem takes a lot of spaces to prove that the gradient of the policy $\pi_{\theta}$ in the direction to improve accumulated returns is:

$J(\theta)\newline=\mathbb{E}_{s,a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)] \newline=\mathbb{E}_{s \sim \pi_\theta}[ \mathbb{E}_{a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)]]\newline=\mathbb{E}_{s\sim\pi_\theta} [\int \pi_\theta(a|s) Q^{\pi_\theta}(s,a) da]$

$\nabla_{\theta} J(\theta) \newline= \mathbb{E}_{s\sim\pi_\theta} [\int \nabla \pi_\theta(a|s) Q^{\pi_\theta}(s,a) da] \quad\quad \text{Treat } Q^{\pi_\theta}(s,a) \text{ as non-differentiable} \newline= \mathbb{E}_{s\sim\pi_\theta} [\int \pi_\theta(a|s) \frac{\nabla \pi_\theta(a|s)}{\pi_\theta(a|s)} Q^{\pi_\theta}(s,a) da] \newline= \mathbb{E}_{s, a \sim \pi_\theta} [Q^{\pi_\theta}(s,a) \nabla_\theta log \pi_\theta(a|s)] \newline \approx \frac{1}{N} [G_t \nabla_\theta log \pi_\theta(a_t|s_t)] \quad \quad s_t, a_t \sim \pi_\theta$
where $G_t$ is the accumulated return beginning from step $t$ from real samples.

Note that the above gradient is only for on-policy policy gradient, because $s_t, a_t \sim \pi_\theta$ . How can we derive the gradient for off-policy policy gradient, i.e., $s_t, a_t \sim \pi_b$ where $\pi_b$ is a different behavior policy? I think the simplest way to derive it is to connect importance sampling with policy gradient.

A quick introduction of importance sampling [2]: estimating a quantity under a distribution is equivalently estimating it under another different distribution with an importance sampling weight, i.e., $\mathbb{E}_{p(x)}[x]=\mathbb{E}_{q(x)}[\frac{q(x)}{p(x)}x]$ . This comes handy when you can’t collect data using $p(x)$ but you can still compute $p(x)$ when $x$ is sampled from $q(x)$ .

In the case of off-policy policy gradient, $J(\theta)$ becomes “the value function of the target policy, averaged over the state distribution of the behavior policy” (from DPG paper [6]):

$J(\theta)\newline=\mathbb{E}_{s\sim\pi_b}\left[\mathbb{E}_{a \sim \pi_\theta} [Q^{\pi_\theta}(s,a)] \right] \newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\pi_\theta(a|s)}{\pi_b(a|s)}Q^{\pi_b}(s,a)]$

$\nabla_{\theta} J(\theta) \newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\nabla_\theta \pi_\theta(a|s)}{\pi_b(a|s)} Q^{\pi_b}(s,a)] \quad\quad \text{Again, treat } Q^{\pi_b}(s,a) \text{ as non-differentiable}\newline=\mathbb{E}_{s,a \sim \pi_b} [\frac{\pi_\theta(a|s)}{\pi_b(a|s)} Q^{\pi_b}(s,a) \nabla_\theta log \pi_\theta(a|s)] \newline \approx \frac{1}{N}[\frac{\pi_\theta(a_t|s_t)}{\pi_b(a_t|s_t)} G_t \nabla_\theta log \pi_\theta(a_t|s_t)] \quad\quad s_t, a_t \sim \pi_b$

As we know adding a state-dependent baseline in on-policy policy gradient would reduce the variance of gradient [4] and not introduce bias. Based on my proof, adding a state-dependent baseline in off-policy policy gradient will not introduce bias either:

$\mathbb{E}_{s,a \sim \pi_b} \left[\frac{\pi_\theta(a|s)}{\pi_b(a|s)} b(s) \nabla_\theta log \pi_\theta(a|s)\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \cdot \mathbb{E}_{a \sim \pi_b}\left[\frac{\pi_\theta(a|s)}{\pi_b(a|s)} \nabla_\theta log \pi_\theta(a|s)\right]\right] \newline = \mathbb{E}_{s \sim \pi_b}\left[b(s) \int \pi_b(a|s) \nabla_\theta \frac{\pi_\theta(a|s)}{\pi_b(a|s)} da\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \int \nabla_\theta \pi_\theta(a|s) da\right]\newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \nabla_\theta \int \pi_\theta(a|s) da\right] \newline=\mathbb{E}_{s \sim \pi_b}\left[b(s) \nabla_\theta 1 \right] \newline=0$

You have probably noticed that during the derivation in on-policy policy gradient, we treat $Q^{\pi_\theta}(s,a)$ as non-differentiable with regard to $\theta$ . However $Q^{\pi_\theta}(s,a)$ is indeed affected by $\pi_\theta$ because it is the returns of the choices made by $\pi_\theta$ . I am not sure if treating $Q^{\pi_\theta}(s,a)$ differentiable would help improve performance, but there are definitely papers doing so in specific applications. One such an example is seq2slate [5] (where, in their notations, $\pi$ refers to actions, $x$ refers to states, and $\mathcal{L}_\pi(\theta)$ is the same as our $Q^{\pi_\theta}(s,a)$ ):

If we adapt Eqn. 8 to the off-policy setting, we have (the first three lines would be the same):

$\nabla_\theta \mathbb{E}_{\pi \sim p_\theta(\cdot|x)} \left[ \mathcal{L}_\pi(\theta)\right] \newline= \nabla_\theta \sum\limits_\pi p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\newline=\sum\limits_\pi \left[ \nabla_\theta p_\theta(\pi|x) \cdot \mathcal{L}_\pi(\theta)+p_\theta(\pi|x) \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=p_b(\pi|x) \cdot \sum\limits_\pi \left[ \frac{\nabla_\theta p_\theta(\pi|x)}{p_b(\pi|x)} \cdot \mathcal{L}_\pi(\theta)+\frac{p_\theta(\pi|x)}{p_b(\pi|x)} \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=\mathbb{E}_{\pi\sim p_b(\cdot|x)}\left[\frac{1}{p_b(\pi|x)}\nabla_\theta\left(p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\right)\right]$

If you follow the same rewriting trick to rewrite Eqn. 8, we can get another form of gradient in the on-policy setting:

$\nabla_\theta \mathbb{E}_{\pi \sim p_\theta(\cdot|x)} \left[ \mathcal{L}_\pi(\theta)\right] \newline= \nabla_\theta \sum\limits_\pi p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\newline=\sum\limits_\pi \left[ \nabla_\theta p_\theta(\pi|x) \cdot \mathcal{L}_\pi(\theta)+p_\theta(\pi|x) \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=p_\theta(\pi|x) \cdot \sum\limits_\pi \left[ \frac{\nabla_\theta p_\theta(\pi|x)}{p_\theta(\pi|x)} \cdot \mathcal{L}_\pi(\theta)+\frac{p_\theta(\pi|x)}{p_\theta(\pi|x)} \cdot \nabla_\theta \mathcal{L}_\pi(\theta) \right]\newline=\mathbb{E}_{\pi\sim p_\theta(\cdot|x)}\left[\frac{1}{p_\theta(\pi|x)}\nabla_\theta\left(p_\theta(\pi|x)\mathcal{L}_\pi(\theta)\right)\right]$
, where in the last few equations, $p_\theta$ not followed by $\nabla_\theta$ is treated as non-differentiable.

Again, I’d like to disclaim that I don’t really know whether we should just make the policy differentiable (policy gradient) or make both the policy and return differentiable (seq2slate Eqn. 8). I’ll report back if I have any empirical findings.

————————— Update 2020.7 ——————-

Another topic to consider is constrained optimization in off-policy policy gradient. I am using notations closer to my real-world usage. Assume we are optimizing a policy’s parameters using data collected by another policy to maximize some reward function $R(s,a)$ (i.e., one-step optimization, $R(s,a)>0 \text{ for } \forall s,a$ ), with the constraint that the policy should also achieve at least some amount of $S$ in another reward type $Q(s,a)$ :
$argmax_\theta \;\; \frac{1}{n} \sum\limits_{i=1}^n R_i\frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)}$
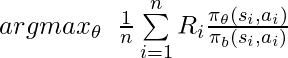
subject to 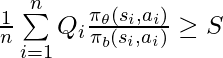$\frac{1}{n}\sum\limits^{n}_{i=1} Q_i \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} \geq S$

Writing it in a standard optimization format, we have: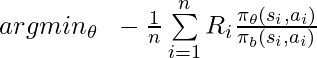
$argmin_\theta \;\; -\frac{1}{n} \sum\limits_{i=1}^n R_i\frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)}$
subject to 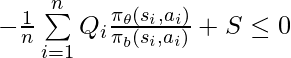$-\frac{1}{n}\sum\limits^{n}_{i=1} Q_i \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} + S \leq 0$

Now we can solve this optimization problem using Lagrangian multiplier. Suppose there is a non-negative multiplier $\lambda \geq 0$ . The augmented objective function becomes the original objective plus an additional penalty, which makes infeasible solutions sub-optimal:
$\arg\max\limits_\lambda \arg\min\limits_\theta \mathcal{L}(\theta, \lambda) \newline= -\frac{1}{n} \sum\limits_{i=1}^n R_i\frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} + \lambda \left(-\frac{1}{n}\sum\limits^{n}_{i=1} Q_i \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} + S \right) \newline = -\frac{1}{n} \sum\limits_{i=1}^n (R_i + \lambda Q_i) \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} + \lambda S$

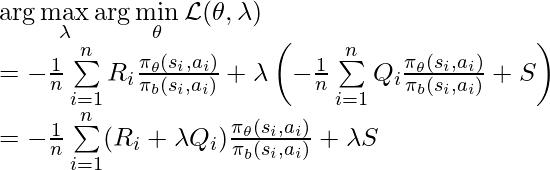
In simpler problems we can just find the saddle point where $\frac{\partial \mathcal{L}}{\partial \theta}=0$ and $\frac{\partial \mathcal{L}}{\partial \lambda}=0$ . However, our problem could be in a large scale that it is not feasible to find the saddle point easily. Note that one cannot use stochastic gradient descent to find the saddle point because saddle points are not local minima [8].

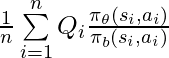Following the idea in [7], what we can show is that if we try to optimize $\theta$ under different $\lambda$ ‘s, then $\frac{1}{n}\sum\limits^{n}_{i=1} Q_i \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)}$ would have a monotonic trend:

Suppose 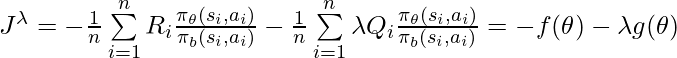$J^\lambda = -\frac{1}{n}\sum\limits_{i=1}^n R_i\frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} -\frac{1}{n}\sum\limits_{i=1}^n \lambda Q_i \frac{\pi_\theta(s_i, a_i)}{\pi_b(s_i, a_i)} = -f(\theta)-\lambda g(\theta)$

For any arbitrary two $\lambda$ ‘s: $\lambda_a < \lambda_b$ , we have:
$\theta_a = argmin_\theta J^{\lambda_a}$
$\theta_b = argmin_\theta J^{\lambda_b}$

Therefore,
$-f(\theta_a) - \lambda_a g(\theta_a) < -f(\theta_b) - \lambda_a g(\theta_b)$
$-f(\theta_b) - \lambda_b g(\theta_b) < -f(\theta_a) - \lambda_b g(\theta_a)$

Adding both sides will keep the inequality hold:
$-f(\theta_a) - \lambda_a g(\theta_a)-f(\theta_b) - \lambda_b g(\theta_b) < -f(\theta_b) - \lambda_a g(\theta_b)-f(\theta_a) - \lambda_b g(\theta_a)$
$\lambda_a g(\theta_a) + \lambda_b g(\theta_b) > \lambda_a g(\theta_b) + \lambda_b g(\theta_a)$
$(\lambda_a - \lambda_b) g(\theta_a) > (\lambda_a - \lambda_b) g(\theta_b)$
$g(\theta_a) < g(\theta_b)$ (because $\lambda_a - \lambda_b < 0$ the inequality changes direction)

This theorem immediately implies that if we optimize $\theta$ using normal off-policy policy gradient with reward in the form of $R_i + \lambda Q_i$ , we are essentially doing constrained optimization. The larger $\lambda$ we use, the more rigid the constraint is. While using a combined reward shape like $R_i + \lambda Q_i$ looks a naive way to balance trade-offs, I never thought it could link to constrained optimization in this way!

The Lagrangian Multiplier optimization procedure above is taken referenced at [9].

————————— Update 2020.7 part (2) ——————-

Note that one cannot use stochastic gradient descent to find the saddle point because saddle points are not local minima [8].

This sentence is actually controversial. From [10] Section 3, we can see that we can still use stochastic gradient update to find the saddle point: for $\lambda$ , we use gradient ascent; for $\theta$ we use gradient descent. Second, we can convert $\mathcal{L}(\theta, \lambda)$ to yet another problem for minimizing the magnitude of the gradient of both $\theta$ and $\lambda$ [11] . The intuition is that the closer to the saddle point, the smaller magnitude of the gradient of $\theta$ and $\lambda$ . Therefore, we can perform stochastic gradient descent on the magnitude of gradient.