In this post, I am sharing my understanding regarding Deterministic Policy Gradient Algorithm (DPG) [1] and its deep-learning version (DDPG) [2].
We have introduced policy gradient theorem in [3, 4]. Here, we briefly recap. The objective function of policy gradient methods is:
$latex J(\theta)=\sum\limits_{s \in S} d^\pi(s) V^\pi(s)=\sum\limits_{s \in S} d^\pi(s) \sum\limits_{a \in A} \pi(a|s) Q^\pi(s,a), &s=2$
where $latex \pi$ represents $latex \pi_\theta$, $latex d^\pi(s)$ is the stationary distribution of Markov chain for $latex \pi$, $latex V^\pi(s)=\mathbb{E}_{a \sim \pi}[G_t|S_t=s]$, and $latex Q^{\pi}(s,a)=\mathbb{E}_{a \sim \pi}[G_t|S_t=s, A_t=a]$. $latex G_t$ is accumulated rewards since time step $latex t$: $latex G_t=\sum^\infty_{k=0}\gamma^k R_{t+k}$.
Policy gradient theorem proves that the gradient of policy parameters with regard to $latex J(\theta)$ is:
$latex \nabla_\theta J(\theta) = \mathbb{E}_{\pi}[Q^\pi(s,a)\nabla_\theta ln \pi_\theta(a|s)] &s=2$
More specifically, the policy gradient theorem we are talking about is stochastic policy gradient theorem because at each state the policy outputs a stochastic action distribution $latex \pi(s|a)$.
However, the policy gradient theorem implies that policy gradient must be calculated on-policy, as $latex \mathbb{E}_{\pi}:=\mathbb{E}_{s\sim d^{\pi}, a\sim \pi}$ means the state and action distribution is generated by following $latex \pi_\theta$.
If the training samples is generated by some other behavioral policy $latex \beta$, then the objective function becomes:
$latex J(\theta)=\sum\limits_{s \in S} d^\beta(s) V^\pi(s)=\sum\limits_{s \in S} d^\beta(s) \sum\limits_{a \in A} \pi(a|s) Q^\pi(s,a), &s=2$
and we must rely on importance sampling to calculate the policy gradient [7,8]:
$latex \nabla_\theta J(\theta) = \mathbb{E}_{s\sim d^\beta}[\sum\limits_{a\in A}\nabla_\theta \pi(a|s) Q^\pi(s,a) + \pi(a|s)\nabla_\theta Q^\pi(s,a)] \newline \approx \mathbb{E}_{s\sim d^\beta}[\sum\limits_{a\in A}\nabla_\theta \pi(a|s) Q^\pi(s,a)] \newline =\mathbb{E}_{\beta}[\frac{\pi_\theta(a|s)}{\beta(a|s)}Q^\pi(s,a)\nabla_\theta ln \pi_\theta(a|s)] &s=2$
where $latex \mathbb{E}_{\beta}:=\mathbb{E}_{s\sim d^\beta, a\sim\beta}$
However, using importance sampling $latex \frac{\pi_\theta(a|s)}{\beta(a|s)}$ could incur some learning difficulty problems [5]:
What DPG proposes is that we design a policy that outputs actions deterministically: $latex a = \mu_\theta(s)$, thus $latex J(\theta)$ would only have integration (or sum) over state distribution and get rid of importance sampling, which makes learning potentially easier:
$latex J(\theta)=\sum\limits_{s \in S} d^\beta(s) V^\mu(s)=\sum\limits_{s \in S} d^\beta(s) Q^\mu(s, \mu_\theta(s)) &s=2$
Writing the above formula in integration (rather than discrete sum), we get:
$latex J(\theta)=\int\limits_S d^\beta(s) V^\mu(s) ds=\int\limits_{S} d^\beta(s) Q^\mu(s, \mu_\theta(s)) ds &s=2$
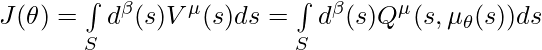
And the gradient of $latex J(\theta)$ is:
$latex \nabla_\theta J(\theta) = \int\limits_S d^\beta(s) \nabla_\theta Q^\mu(s, \mu_\theta(s)) ds \approx \mathbb{E}_\beta [\nabla_\theta \mu_\theta(s) \nabla_a Q^\mu(s,a)|_{a=\mu_\theta(s)}] &s=2$
This immediately implies that $latex \theta$ can be updated off policy. Because we only need to sample $latex s \sim d^\beta(s)$, then $latex \nabla J(\theta)$ can be calculated without knowing what action the behavior policy $latex \beta$ took (we only need to know what the training policy would take, i.e., $latex a=\mu_\theta(s)$). We should also note that there is an approximation in the formula of $latex \nabla_\theta J(\theta)$, because $latex \nabla_\theta Q^u(s,\mu_\theta(s))&s=2$ cannot be applied chain rules easily since even you replace $latex \mu_\theta(s))$ with $latex a$, the $latex Q$ function itself still depends on $latex \theta$.
Updating $latex \theta$ is one part of DPG. The other part is fitting a Q-network with parameter $latex \phi$ on the optimal Q-function of policy governed by $latex \theta$. This equates to update according to mean-squared Bellman error (MSBE) [10], which is the same as in Q-Learning.
I haven’t read the DDPG paper [2] thoroughly but based on my rough understanding, it adds several tricks when dealing with large inputs (such as images). According to [9]’s summary, DDPG introduced three tricks:
- add batch normalization to normalize “every dimension across samples in one minibatch”
- add noise in the output of DPG such that the algorithm can explore
- soft update target network
References
[3] Notes on “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor”: https://czxttkl.com/?p=3497
[4] Policy Gradient: https://czxttkl.com/?p=2812
[9] https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html#ddpg
[10] https://spinningup.openai.com/en/latest/algorithms/ddpg.html#the-q-learning-side-of-ddpg