LambdaMART [7] is one of Learn to Rank algorithms. It emphasizes on fitting on the correct order of a list, which contains all documents returned by a query and marked as different relevance. It is a derivation/combination of RankNet, LambdaRank and MART (Multiple Addictive Regression Tree).
For me, the most helpful order to approach LambdaMART is to understand: 1. MART; 2. RankNet; 3. LambdaRank; and 4. LambdaMART. [4] actually aligns with my order to introduce LambdaMART. (Sidenote: another good resource to learn MART is [8])
1. MART

Above is an illustration plot for one regression tree. If data of different labels actually come from disjoint feature spaces, then one regression tree would be enough. However, there are many situations where data do come from interleaved feature spaces. Hence, it is natural to propose using multiple regression trees to differentiate irregular feature subspaces and make predictions.
Now, suppose MART’s prediction function is 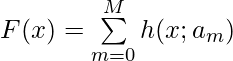 , where each
, where each ![]() is one regression tree’s output and
is one regression tree’s output and ![]() are the parameters of that tree. Generally speaking, each regression tree has K-terminal nodes. Hence
are the parameters of that tree. Generally speaking, each regression tree has K-terminal nodes. Hence ![]() contains
contains ![]() , which are the K feature subspaces that divide data, and
, which are the K feature subspaces that divide data, and ![]() , which are the predicted outputs of data belonging to
, which are the predicted outputs of data belonging to ![]() .
. ![]() can be represented as:
can be represented as: 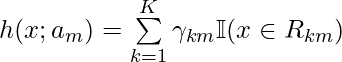
![]() are iteratively learned to fit to the training data:
are iteratively learned to fit to the training data:
- Set
 to initial guess
to initial guess - for each
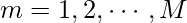 , we learn optimal feature space divisions
, we learn optimal feature space divisions 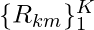
- Based on the learned
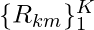 , the prediction value of each
, the prediction value of each 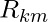 (leaf) is deterministically fixed as:
(leaf) is deterministically fixed as: 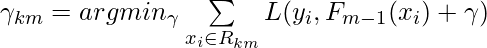
Although [4] doesn’t provide details for learning ![]() , I guess they should be very similar to what adopted in normal decision trees. One possible criteria could be to minimize the total loss:
, I guess they should be very similar to what adopted in normal decision trees. One possible criteria could be to minimize the total loss: 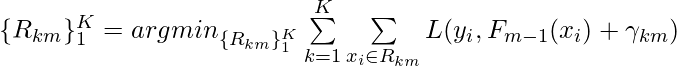 . (If using this criteria,
. (If using this criteria, ![]() and
and ![]() are actually learned simultaneously)
are actually learned simultaneously)
[4] provides an example to illustrate the iterative learning process. The dataset contains data points in 2 dimensions and labels ![]() . The loss function
. The loss function ![]() is least square loss. Each regression tree is only a decision stump.
is least square loss. Each regression tree is only a decision stump.
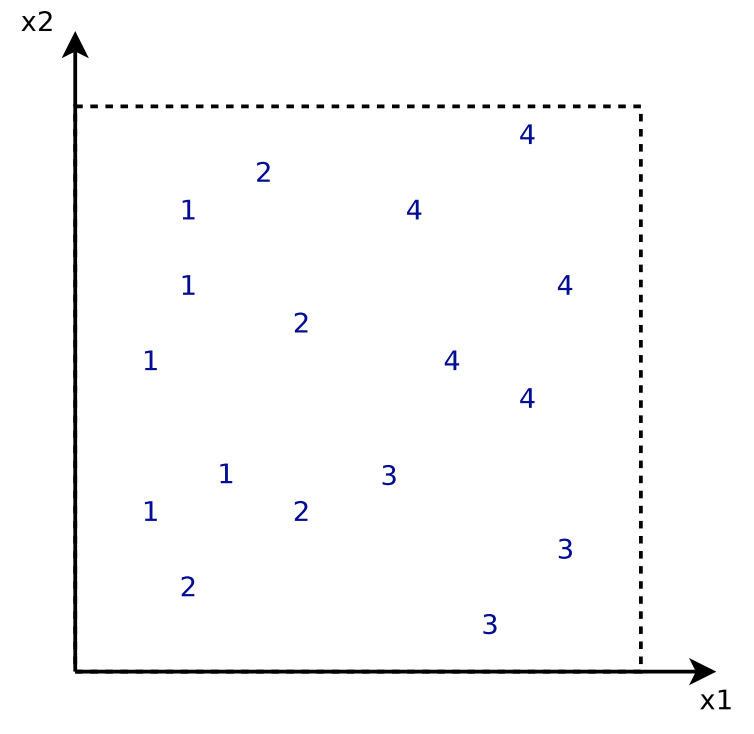
![]() is the simplest predictor that predicts a constant value minimizing the error for all training data.
is the simplest predictor that predicts a constant value minimizing the error for all training data.

After determining ![]() , we start to build
, we start to build ![]() . The cut
. The cut ![]() is determined by some criterion not mentioned. But assuming that
is determined by some criterion not mentioned. But assuming that ![]() has already been obtained, we can then determine each leaf’s prediction output, i.e.,
has already been obtained, we can then determine each leaf’s prediction output, i.e., ![]() :
:
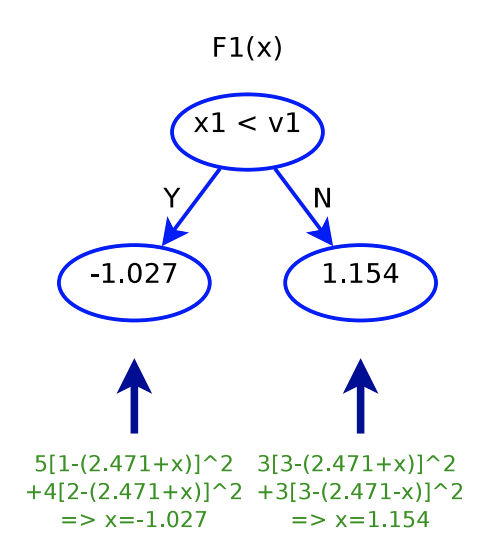
After determining the first and second trees, ![]() . In other words, for
. In other words, for ![]() , the predicted value will be 1.444; for
, the predicted value will be 1.444; for ![]() , the predicted value will be 3.625.
, the predicted value will be 3.625.

Next, determining ![]() will be similar: finding a cut
will be similar: finding a cut ![]() , and then determine
, and then determine ![]() as in step 3.
as in step 3.
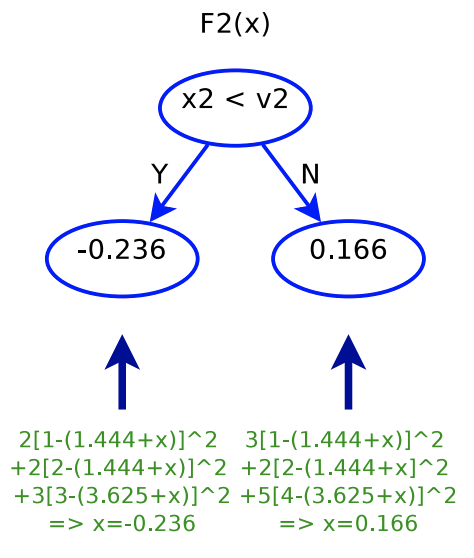
Interestingly, when we fit ![]() , it looks like that we fit a tree with each data point’s label updated as
, it looks like that we fit a tree with each data point’s label updated as ![]() , that is, we are fitting the residual of what previous trees are not able to predict. Below is the plot showing each data point’s original label and its updated label before fitting
, that is, we are fitting the residual of what previous trees are not able to predict. Below is the plot showing each data point’s original label and its updated label before fitting ![]() .
.
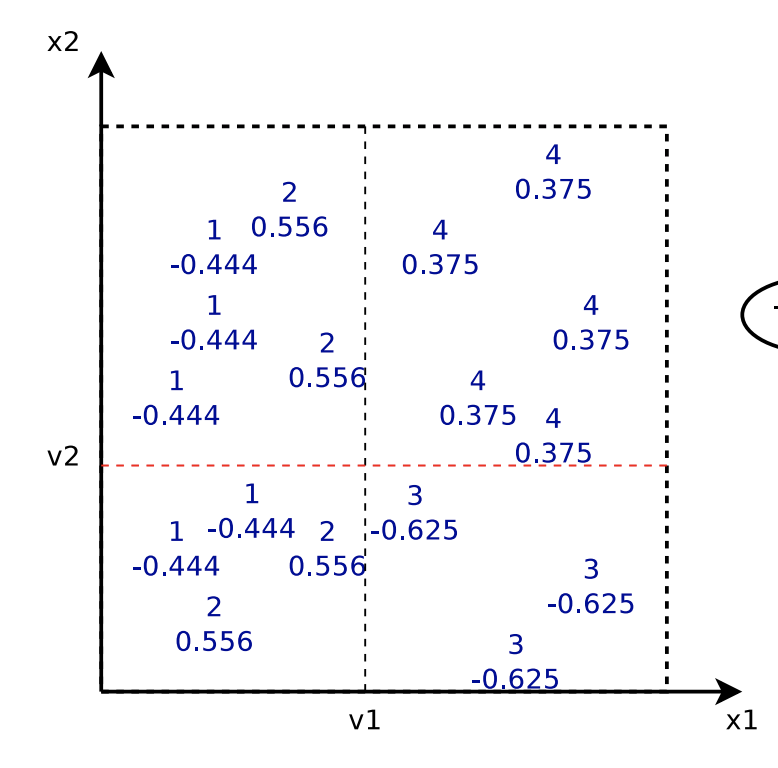
In fact, the fitting process described above is based on the assumption that ![]() is a square loss function. When fitting the
is a square loss function. When fitting the ![]() -th tree, we are fitting the tree to the residual
-th tree, we are fitting the tree to the residual ![]() . Interestingly,
. Interestingly, ![]() . That’s why MART is also called Gradient Boosted Decision Tree because that each tree fits the gradient of the loss.
. That’s why MART is also called Gradient Boosted Decision Tree because that each tree fits the gradient of the loss.
To be more general and mathematical, when we learn ![]() and
and ![]() in the
in the ![]() -th iteration, our objective function is:
-th iteration, our objective function is:
![]()
If we take Taylor series of the objective function up to order 2 at 0, we get [10]:
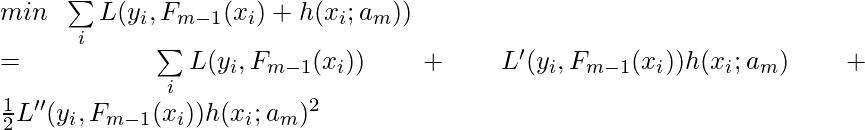
Each time, the new regression tree (![]() and
and ![]() ) should minimize this objective function, which is a quadratic function with regard to
) should minimize this objective function, which is a quadratic function with regard to ![]() . As long as we know
. As long as we know ![]() and
and ![]() , we can learn the best
, we can learn the best ![]() to minimize the objective function.
to minimize the objective function.
Now, back to the previous example, if ![]() is a square loss function
is a square loss function ![]() , then
, then ![]() and
and ![]() . Thus, the objective function becomes:
. Thus, the objective function becomes:

This is not different than ![]() . That’s why in the above fitting process, it seems like we are fitting each new tree to the residual between the real label and previous trees’ output. In another equivalent perspective, we are fitting each new tree to the gradient
. That’s why in the above fitting process, it seems like we are fitting each new tree to the residual between the real label and previous trees’ output. In another equivalent perspective, we are fitting each new tree to the gradient ![]() .
.
The loss function ![]() can take many kinds of forms, making MART a general supervised learning model. When MART is applied on classification problems, then the loss function for each data point
can take many kinds of forms, making MART a general supervised learning model. When MART is applied on classification problems, then the loss function for each data point ![]() is
is ![]() , where
, where ![]() is the predicted probability
is the predicted probability ![]() . The regression trees’ output is used to fit the logit of
. The regression trees’ output is used to fit the logit of ![]() , i.e.,
, i.e.,
![]()
If we formulate all things in ![]() , then we have:
, then we have:
![]() See [11])
See [11])
![]() (See [12])
(See [12])
After such formulation, it will be easy to calculate ![]() and
and ![]() .
.
2. RankNet
We finished introducing MART. Now let’s talk about RankNet and LambdaMART. Starting from now, we follow the notations from [7]:
(Table from [9])
After reading the first three chapters of [7], you probably reach the plot:

The plot illustrates the motivation for the invent of LambdaRank based on RankNet. In RankNet, the cost function is an easily defined, differentiable function:
![]()
If ![]() ,
, ![]() ; if
; if ![]() ,
, ![]() . The intuition of this cost function is that the more consistent the relative order between
. The intuition of this cost function is that the more consistent the relative order between ![]() and
and ![]() is with
is with ![]() , the smaller
, the smaller ![]() will be.
will be.
Since the scores ![]() and
and ![]() are from a score function of parameters
are from a score function of parameters ![]() , the cost function
, the cost function ![]() is a function of
is a function of ![]() too. Our goal is to adjust
too. Our goal is to adjust ![]() to minimize
to minimize ![]() . Therefore, we arrive at the gradient of
. Therefore, we arrive at the gradient of ![]() regarding
regarding ![]() (using just one parameter
(using just one parameter ![]() as example):
as example):
![]() , where
, where ![]() . (This is from Eqn. 3 in [7].)
. (This is from Eqn. 3 in [7].)
![]() is derived from a pair of URLs
is derived from a pair of URLs ![]() and
and ![]() . For each document, we can aggregate to
. For each document, we can aggregate to ![]() by taking into account of all its interaction with other documents:
by taking into account of all its interaction with other documents:
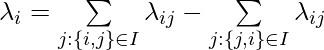
Based on the derivation from Section 2.1 in [7], the update rule of score function parameter ![]() can be eventually expressed by
can be eventually expressed by ![]() :
:
![]()
![]() can be seen as the force to drive high and low of
can be seen as the force to drive high and low of ![]() from document
from document ![]() . Here is how one can understand the effect of
. Here is how one can understand the effect of ![]() through a simple but wordy example. Suppose for a document
through a simple but wordy example. Suppose for a document ![]() which only has one pair
which only has one pair ![]() (
(![]() ). Assume in one particular update step, we have
). Assume in one particular update step, we have ![]() , i.e., an increase of
, i.e., an increase of ![]() will cause
will cause ![]() to increase if everything else is fixed. Therefore,
to increase if everything else is fixed. Therefore, ![]() assuming
assuming ![]() . According to the update rule
. According to the update rule ![]() , immediately we know that
, immediately we know that ![]() is going increase further to increase
is going increase further to increase ![]() . Nevertheless, depending on whether
. Nevertheless, depending on whether ![]() or
or ![]() , the scale of
, the scale of ![]() would be different. If
would be different. If ![]() , that is, the current calculated scores has a relative order consistent with the label, then
, that is, the current calculated scores has a relative order consistent with the label, then ![]() . On the other hand, if
. On the other hand, if ![]() , that is, the current calculated scores are inconsistent with the label,
, that is, the current calculated scores are inconsistent with the label, ![]() will become relatively large (
will become relatively large (![]() 1).
1).
3. LambdaMART
The problem of RankNet is that sometimes ![]() does not perfectly correlate to the force we want to drag the document to the ideal place. On the right of the example plot, the black arrows denote
does not perfectly correlate to the force we want to drag the document to the ideal place. On the right of the example plot, the black arrows denote ![]() the blue documents are assigned. However, if we want to use metrics that emphasize on the top few results (e.g., NDCG/ERR) we want
the blue documents are assigned. However, if we want to use metrics that emphasize on the top few results (e.g., NDCG/ERR) we want ![]() to correlate with the red arrows. Unfortunately, many metrics like NDCG and ERR are not easy to come up with a well-formed cost function
to correlate with the red arrows. Unfortunately, many metrics like NDCG and ERR are not easy to come up with a well-formed cost function ![]() . Recall the cost function of RankNet: as long as
. Recall the cost function of RankNet: as long as ![]() and
and ![]() are consistent with
are consistent with ![]() ,
, ![]() will be low regardless the absolution positions that
will be low regardless the absolution positions that ![]() and
and ![]() appear. The fortunate part is that we do not need to know
appear. The fortunate part is that we do not need to know ![]() when we train the model: all we need to know is
when we train the model: all we need to know is ![]() and we can design our own
and we can design our own ![]() for those not well-formed cost functions. Thus, the core idea of LambdaRank is to define
for those not well-formed cost functions. Thus, the core idea of LambdaRank is to define ![]() by:
by:
![]()
where ![]() is the change after swapping
is the change after swapping ![]() and
and ![]() of any measure you apply. This swap takes place in the sorted list of all documents according to their current calculated scores, and all documents’ positions are kept fixed except the two documents being swapped.
of any measure you apply. This swap takes place in the sorted list of all documents according to their current calculated scores, and all documents’ positions are kept fixed except the two documents being swapped.
Now, if the model we are training contains parameters that form differential score functions then we can easily apply the update rule on those parameters like we talked about in <2. RankNet>: ![]()
However, if we are going to train MART, then we need to train it according to its iterative process, which only requires knowing ![]() . This finally arrives at the LambdaMART algorithm:
. This finally arrives at the LambdaMART algorithm:

Note that in LambdaMART we usually define ![]() in the way that fitting it is equivalent to maximizing some utility function
in the way that fitting it is equivalent to maximizing some utility function ![]() . Therefore, the Newton step to calculate
. Therefore, the Newton step to calculate ![]() is actually doing gradient ascent. Recall that in <1. MART> section the objective that each MART tree optimizes for is:
is actually doing gradient ascent. Recall that in <1. MART> section the objective that each MART tree optimizes for is:
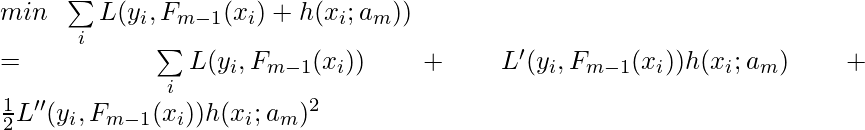
In the LambdaMART algorithm, ![]() corresponds to
corresponds to ![]() and
and ![]() corresponds to
corresponds to ![]() .
.
Reference
[1] http://www.cnblogs.com/wowarsenal/p/3900359.html
[2] https://www.quora.com/search?q=lambdamart
[3] https://liam0205.me/2016/07/10/a-not-so-simple-introduction-to-lambdamart/
[5] https://www.slideshare.net/Julian.Qian/learning-to-rank-an-introduction-to-lambdamart
[6] https://en.wikipedia.org/wiki/Newton%27s_method
[8] https://www.youtube.com/watch?v=IXZKgIsZRm0
[9] https://www.slideshare.net/Julian.Qian/learning-to-rank-an-introduction-to-lambdamart
[10] http://xgboost.readthedocs.io/en/latest/model.html
[11] https://stats.stackexchange.com/questions/157870/scikit-binomial-deviance-loss-function
[13] http://dasonmo.cn/2019/02/08/from-ranknet-to-lambda-mart/
Update 2020/02/22:
This reference contains an example of computing ![]() using NDCG metric:
using NDCG metric:
[14] http://dasonmo.cn/2019/02/08/from-ranknet-to-lambda-mart/