Recently, I am studying a basic contextual bandit algorithm called Logistic Regression Bandit, which is also known as Bayesian Logistic Regression. It all starts from the paper “An Empirical Evaluation of Thompson Sampling” [1]. In Algorithm 3 in the paper, the authors gives the pseudo-code for how to train the Logistic Regression Bandit, assuming its weights are from a Gaussian distribution with a diagonal covariance matrix:

When I first read it, my biggest confusion is Laplace approximation – why is it used in training a Bayesian logistic regression? Now, let’s dig into how Laplace approximation comes into play.
Let’s first review the set up of a Bayesian logistic regression. Suppose we have a feature space ![]() . We have a dataset
. We have a dataset ![]() which contains tuples of
which contains tuples of ![]() for
for ![]() . These are observed features and labels. If we apply a Bayesian logistic regression on such data, the logistic regression will have a weight vector of the same dimension as the features:
. These are observed features and labels. If we apply a Bayesian logistic regression on such data, the logistic regression will have a weight vector of the same dimension as the features: ![]() . The prediction function is a sigmoid function:
. The prediction function is a sigmoid function: ![]() .
.
Because it is a Bayesian logistic regression, we need to estimate a posterior probability distribution for ![]() given the observation
given the observation ![]() ,
, ![]() . We assume that
. We assume that ![]() come from a multi-dimensional Gaussian distribution with a diagonal covariance matrix. This is the same as what Algorithm 3’s notation implies:
come from a multi-dimensional Gaussian distribution with a diagonal covariance matrix. This is the same as what Algorithm 3’s notation implies: ![]() .
.
We can also get the likelihood function 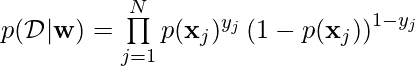
Using the Bayesian Theorem, we can derive (the notations adapted from [2] (slides page 9~12) to the notations in this post):
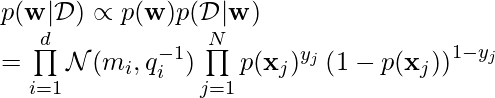
Now, here is how Lapalace Approximation [3] comes into play. The goal of Lapalace Approximation is to learn a Gaussian distribution to approximate ![]() , which is not a Gaussian distribution in its exact expression. In other words, if
, which is not a Gaussian distribution in its exact expression. In other words, if ![]() , what would be
, what would be ![]() and
and ![]() ?
?
First, we will take the logarithm on both sides, leading to:
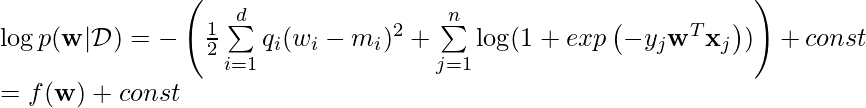
Suppose ![]() achieves maximum
achieves maximum ![]() , which is able to be found using gradient ascent or expressed in a closed formula (I think
, which is able to be found using gradient ascent or expressed in a closed formula (I think ![]() is a concave function but not totally sure). Based on the 2nd-order Taylor expansion at point
is a concave function but not totally sure). Based on the 2nd-order Taylor expansion at point ![]() , we have:
, we have: ![]() . Because
. Because ![]() , we can further simplify to
, we can further simplify to ![]() .
.
![]() can actually be seen as the logarithm of another Gaussian distribution
can actually be seen as the logarithm of another Gaussian distribution ![]() , whose mean is at
, whose mean is at ![]() and variance as
and variance as ![]() , and
, and ![]() absorbs any remaining constants. This is why Algorithm 3 updates
absorbs any remaining constants. This is why Algorithm 3 updates ![]() because
because ![]() is essentially from
is essentially from ![]() that maximizes
that maximizes ![]() , and
, and 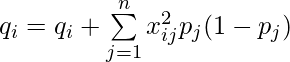 since this is essentially
since this is essentially ![]() .
.
To summarize, Laplace Approximation finds a new Gaussian distribution to approximate ![]() !
!
Reference
[1] An Empirical Evaluation of Thompson Sampling: https://papers.nips.cc/paper/2011/hash/e53a0a2978c28872a4505bdb51db06dc-Abstract.html
[2] https://cs.iupui.edu/~mdundar/CSCIMachineLearning/Lecture12.pdf
[3] https://bookdown.org/rdpeng/advstatcomp/laplace-approximation.html