I haven’t learnt any new loss function for a long time. Today I am going to learn one new loss function, focal loss, which was introduced in 2018 [1].
Let’s start from a typical classification task. For a data 
, where 
is the feature vector and 
is a binary label, a model predicts 
. Then the cross entropy function can be expressed as:
![\[CE(p,y)=-ylog(p)-(1-y)log(1-p)\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-7baa6ecc974f172aed9465e931bd93e9_l3.png "Rendered by QuickLaTeX.com")
If you set
if 
or 
if 
, then 
, as shown in the blue curve below:
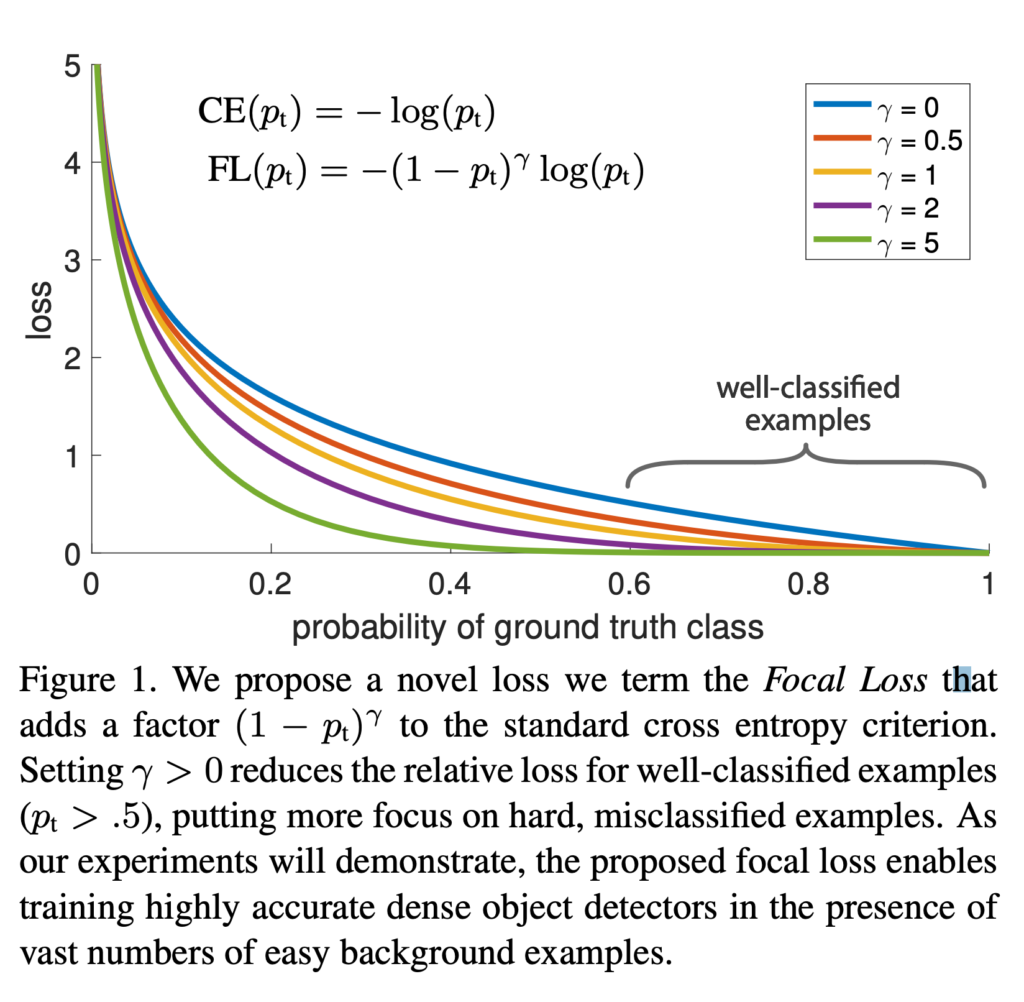
When there are many easy examples, i.e., p_t > 0.6 and the direction matches with the ground-truth label, the loss is small. However, if a dataset has an overwhelmingly large number of such easy examples as in the CV object detection domain, all these small losses add up to overwhelm the hard examples, i.e., those with p_t < 0.6.
Focal loss’s idea is to penalize losses for all kinds of examples, easy or hard, but the easy examples get penalized much more. Focal loss is defined as: 
. By tuning with different 
‘s, you can see that the loss curve gets modulated differently and easy examples’ loss become less and less important.
In the regression domain, we can define the MSE (L2) loss as below, with 
being the absolute prediction. error:
![\[L_2 = | p - y |^2 = l^2\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-f80ece0e582297fc6c50085a3e275683_l3.png "Rendered by QuickLaTeX.com")
Applying the focal loss’s spirit on L_2, you get:
![\[FL\_L_2=l^\gamma \cdot l^2 = l^{\gamma+2}\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-d2b33f6ef1483fe55c37156838aaa028_l3.png "Rendered by QuickLaTeX.com")
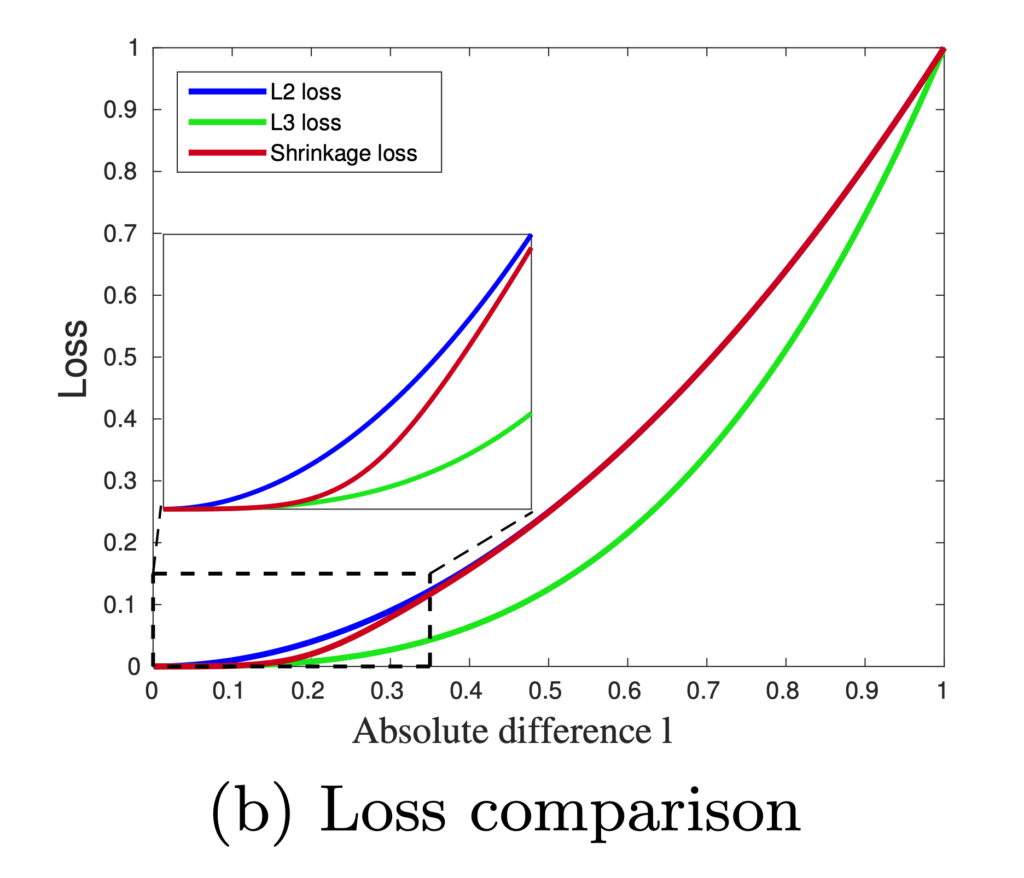
So the focal loss in the regression domain is just a higher-order loss.
[2] takes a step further on the 
by letting 
penalty effective almost only on the easy examples but not on the hard examples. They call it the shrinkage loss:
![\[L_S = \frac{l^2}{1 + exp\left(a\cdot \left( c-l \right)\right)}\]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-60f04910d6082a4a6a347f51491eeac0_l3.png "Rendered by QuickLaTeX.com")
Reference
[1] Focal Loss for Dense Object Detection: https://arxiv.org/pdf/1708.02002.pdf
[2] Deep Regression Tracking with Shrinkage Loss: https://openaccess.thecvf.com/content_ECCV_2018/papers/Xiankai_Lu_Deep_Regression_Tracking_ECCV_2018_paper.pdf
The article introduces the focal loss, a loss function used in classification tasks, particularly for addressing the issue of overwhelming easy examples in datasets like object detection in computer vision. Focal loss penalizes losses for all examples, but easy examples are penalized more, helping to address class imbalance in certain tasks.