Writing this post to share my notes on Trust Region Policy Optimization [2], Proximal Policy Optimization [3], and some recent works leveraging graph neural networks on RL problems.
We start from the objective of TRPO. The expected return of a policy is ![Rendered by QuickLaTeX.com \eta(\pi)=\mathbb{E}_{s_0, a_0, \cdots}[\sum\limits_{t=0}^{\infty}\gamma^t r(s_t)]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-7aaa56488dc12ec0dfe3ddf7febd9a8e_l3.png) . The return of another policy
. The return of another policy ![]() can be expressed as
can be expressed as ![]() and a relative difference term:
and a relative difference term: ![]() , where for any given
, where for any given ![]() ,
, ![]() is called discounted state visitation frequency.
is called discounted state visitation frequency.
To facilitate the optimization process, the authors propose to replace ![]() with
with ![]() . If the new policy
. If the new policy ![]() is close to
is close to ![]() , this approximation is not that bad since the discounted state visitation frequency shouldn’t change too much. Thus
, this approximation is not that bad since the discounted state visitation frequency shouldn’t change too much. Thus ![]() .
.
Using some theorem (See section 3 [2]) we can prove that ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() . The inequality-equality becomes just equality if
. The inequality-equality becomes just equality if ![]() . Therefore,
. Therefore, ![]() . Therefore, we can use algorithm 1 to monotonically improve
. Therefore, we can use algorithm 1 to monotonically improve ![]() .
.

The algorithm 1 can also be understood through the diagram below (from [10]), where we set ![]() .
.
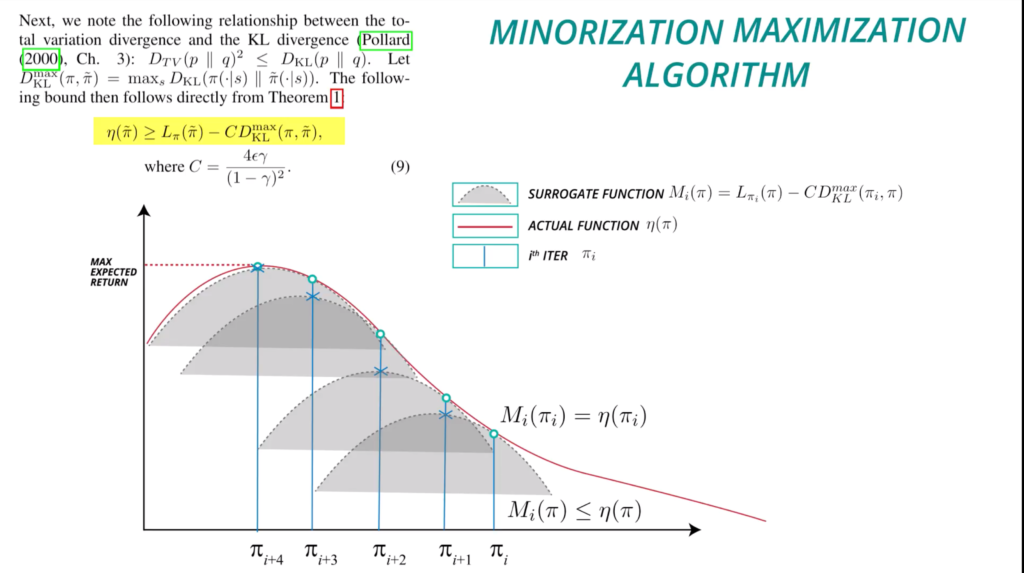
In practice, we parameterize a policy with ![]() , and we move the coefficient
, and we move the coefficient ![]() from the objective to a constraint (the paper argues this could improve the policy in larger steps), and finally we use the average KL divergence between two policies rather than
from the objective to a constraint (the paper argues this could improve the policy in larger steps), and finally we use the average KL divergence between two policies rather than ![]() . Putting these practical treatments together, we get:
. Putting these practical treatments together, we get:
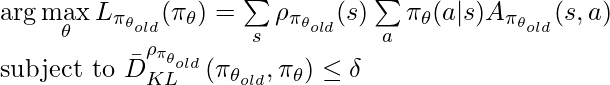
If changing the sum to expectation ![]() , we will need some importance-sampling re-weighting. And in practice, we can estimate Q-values from trajectories more easily than estimating advantages because we would need exhaust all actions at each step to compute advantages. Thus the objective function using empirical samples eventually becomes:
, we will need some importance-sampling re-weighting. And in practice, we can estimate Q-values from trajectories more easily than estimating advantages because we would need exhaust all actions at each step to compute advantages. Thus the objective function using empirical samples eventually becomes:
![Rendered by QuickLaTeX.com \arg\max\limits_{\theta} \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \big[\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} Q_{\pi_{\theta_{old}}}(s,a)\big] \newline \text{subject to } \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}} \big[D_{KL}(\pi_{\theta_{old}}(\cdot|s) \| \pi_{\theta}(\cdot|s))\big]\leq \delta](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-9a1fda6467b2fce611cb38f03ebe4150_l3.png)
Suppose the objective is ![]() . Using Taylor series expansion, we have
. Using Taylor series expansion, we have ![]() .
. ![]() can be seen as a constant and thus can be ignored during optimization.
can be seen as a constant and thus can be ignored during optimization.
And for the constraint, we can also use Taylor series expansion (this is a very common trick to convert KL divergence between two distributions into Taylor series expansion). Suppose ![]() , then
, then ![]() . We know that
. We know that ![]() because it is the KL divergence between the same distribution
because it is the KL divergence between the same distribution ![]() . We can also know that
. We can also know that ![]() because the minimum of KL divergence is 0 and is reached when
because the minimum of KL divergence is 0 and is reached when ![]() hence the derivative at
hence the derivative at ![]() must be 0.
must be 0.
Removing all constant and zero terms, and with two more notations ![]() and
and ![]() , we rewrite the objective function as well as the constraint:
, we rewrite the objective function as well as the constraint:
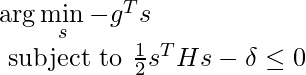
Now the Lagrange Multiplier optimization kicks in. Intuitively, the direction to get to the next ![]() is on the direction that minimizes
is on the direction that minimizes ![]() while stretching the constraint by the most extent (at the moment when the equality of the constraint holds). Denote the Lagrange Multiplier as
while stretching the constraint by the most extent (at the moment when the equality of the constraint holds). Denote the Lagrange Multiplier as ![]() (a single scalar because we only have one constraint) and the auxiliary objective function as
(a single scalar because we only have one constraint) and the auxiliary objective function as ![]() . From Karush-Kuhn-Tucker (KTT) conditions, we want to find a unique
. From Karush-Kuhn-Tucker (KTT) conditions, we want to find a unique ![]() and the local minimum solution
and the local minimum solution ![]() such that:
such that:
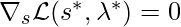

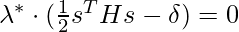
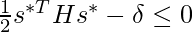 (actually, the equality should hold because
(actually, the equality should hold because 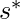 should be obtained at the border of the constraint, although I am not sure how to prove it. This means, as long as we find some non-negative
should be obtained at the border of the constraint, although I am not sure how to prove it. This means, as long as we find some non-negative  such that
such that 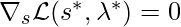 , the first four conditions are satisfied.)
, the first four conditions are satisfied.) 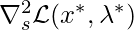 is positive semi-definite.
is positive semi-definite. 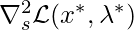 is just
is just 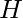 times some constant term. And we know from the fact that: (1)
times some constant term. And we know from the fact that: (1) 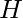 is the Fisher information matrix because it is the Hessian of KL divergence [12]; (2) a Fisher information matrix is positive semi-definite [13].
is the Fisher information matrix because it is the Hessian of KL divergence [12]; (2) a Fisher information matrix is positive semi-definite [13].
Since we don’t have analytical solution for ![]() , we can’t know
, we can’t know ![]() easily. We can start from looking at
easily. We can start from looking at ![]() . Moving
. Moving ![]() to the right side, we have
to the right side, we have ![]() . Here, both
. Here, both ![]() and
and ![]() are unknown to us. But we know that
are unknown to us. But we know that ![]() . Therefore,
. Therefore, ![]() must be in the direction of
must be in the direction of ![]() . How to compute
. How to compute ![]() ? If we just compute
? If we just compute ![]() as pure matrix inversion, we would need
as pure matrix inversion, we would need ![]() time complexity where
time complexity where ![]() is width/height of
is width/height of ![]() . Instead, we can first obtain the solution
. Instead, we can first obtain the solution ![]() of the equation
of the equation ![]() using Conjugate Gradient Method;
using Conjugate Gradient Method; ![]() will be exactly
will be exactly ![]() . We will spend one section below to introduce Conjugate Gradient method but for now just remember Conjugate Gradient method can compute
. We will spend one section below to introduce Conjugate Gradient method but for now just remember Conjugate Gradient method can compute ![]() much faster than
much faster than ![]() as in matrix inversion. Back to our focus: once we get
as in matrix inversion. Back to our focus: once we get ![]() , we will try to take the step size
, we will try to take the step size ![]() that makes the constraint equality hold:
that makes the constraint equality hold: ![]() . Thus the
. Thus the ![]() would be obtained at
would be obtained at ![]() . Therefore,
. Therefore, ![]() . This is exactly one iteration of TRPO update!
. This is exactly one iteration of TRPO update!
We now introduce what the conjugate gradient method is, which is used to find the update direction in TRPO.
Conjugate Gradient Method
My summary is primarily based on [6]. CG is an iterative, efficient method to solve ![]() , which is the solution of the quadratic form
, which is the solution of the quadratic form ![]() . The most straightforward way to solve
. The most straightforward way to solve ![]() is to compute
is to compute ![]() and let
and let ![]() . However, computing
. However, computing ![]() needs
needs ![]() time complexity by Gaussian elimination method, where
time complexity by Gaussian elimination method, where ![]() is the width (or height) of
is the width (or height) of ![]() .
.
If we can’t afford to compute ![]() , the best bet is to rely on iterative methods. We list some notations used across iterative methods before we proceed. The error
, the best bet is to rely on iterative methods. We list some notations used across iterative methods before we proceed. The error ![]() is the distance between the i-th solution
is the distance between the i-th solution ![]() and the real solution
and the real solution ![]() . The residual
. The residual ![]() indicates how far we are from
indicates how far we are from ![]() .
.
Steepest gradient descent with line search works as follows. At solution ![]() , take a step on the direction of
, take a step on the direction of ![]() , and the step size is determined such that the arrival point after the step, which is
, and the step size is determined such that the arrival point after the step, which is ![]() , should have the smallest
, should have the smallest ![]() . This can also be understood as
. This can also be understood as ![]() should be orthogonal to
should be orthogonal to ![]() . The two pictures below help illustrate the idea:
. The two pictures below help illustrate the idea:
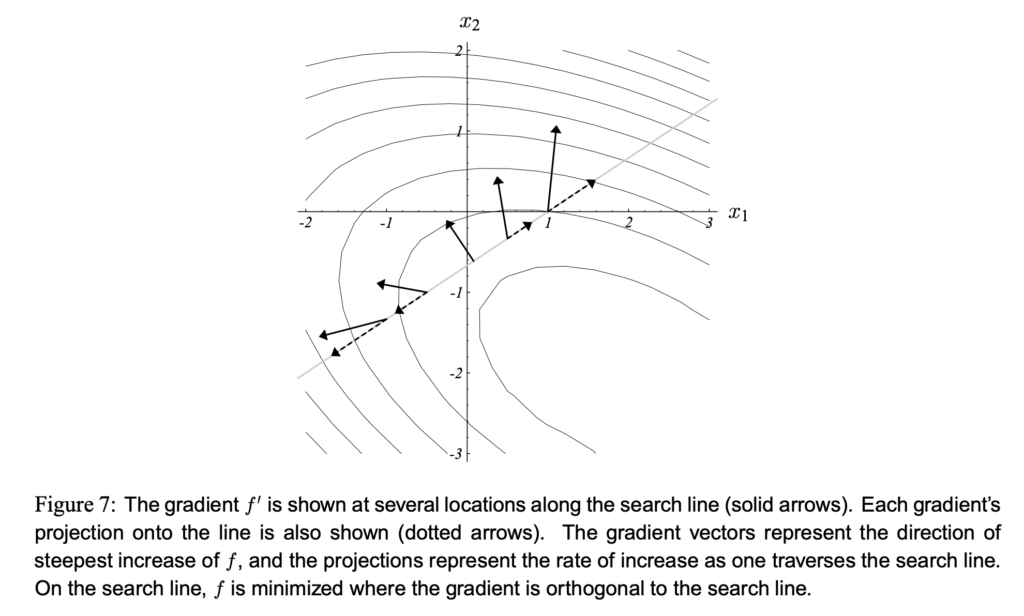
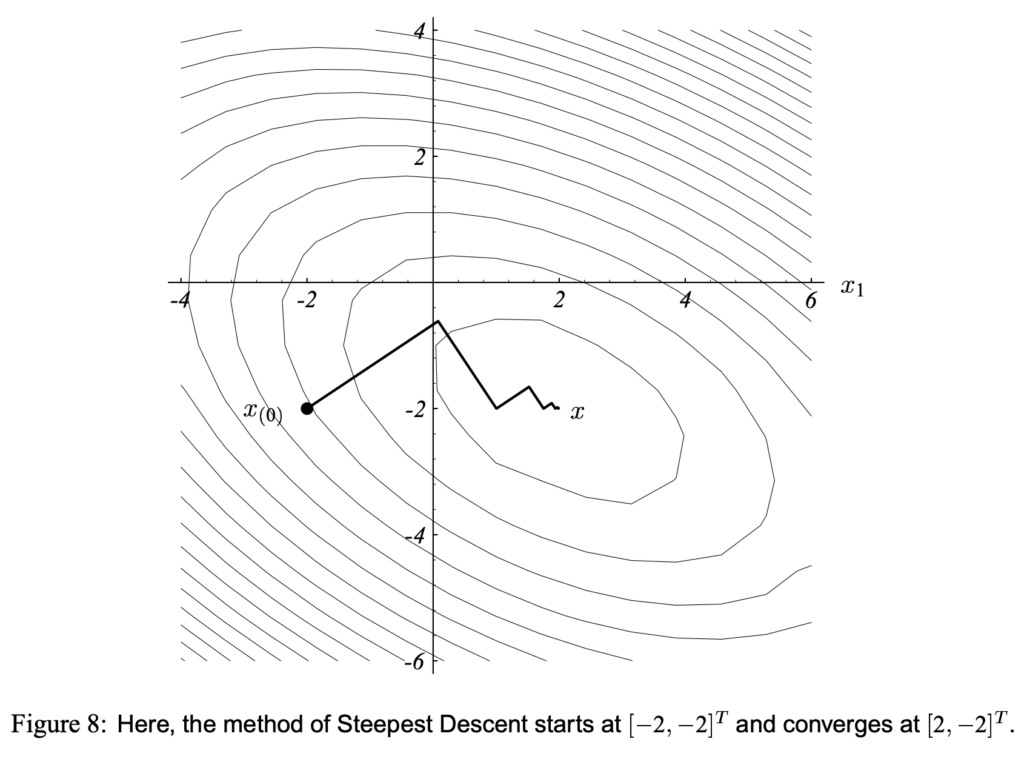
As you can see, the steepest gradient method often takes a zig-zag path to reach the sufficient proximity of the optimal solution. From theories (Section 6.2 in [6]), the number of steps it needs depends on the condition number of ![]() and the starting point
and the starting point ![]() . And from the intuition, the number of steps is no smaller than the number of bases of the solution space. The luckiest situation is that you pick
. And from the intuition, the number of steps is no smaller than the number of bases of the solution space. The luckiest situation is that you pick ![]() which results to all orthogonal steepest gradients in the following steps. Such
which results to all orthogonal steepest gradients in the following steps. Such ![]() can also be thought to have
can also be thought to have ![]() parallel with any of the eigenvectors of
parallel with any of the eigenvectors of ![]() :
:
The idea of conjugate direction methods (conjugate gradient is one of conjugate direction methods) is to enforce the iterations happen exactly ![]() times to reach the optimal solution, where, by our definition,
times to reach the optimal solution, where, by our definition, ![]() is the width (or height) of
is the width (or height) of ![]() and also the number of bases of the solution space.
and also the number of bases of the solution space.
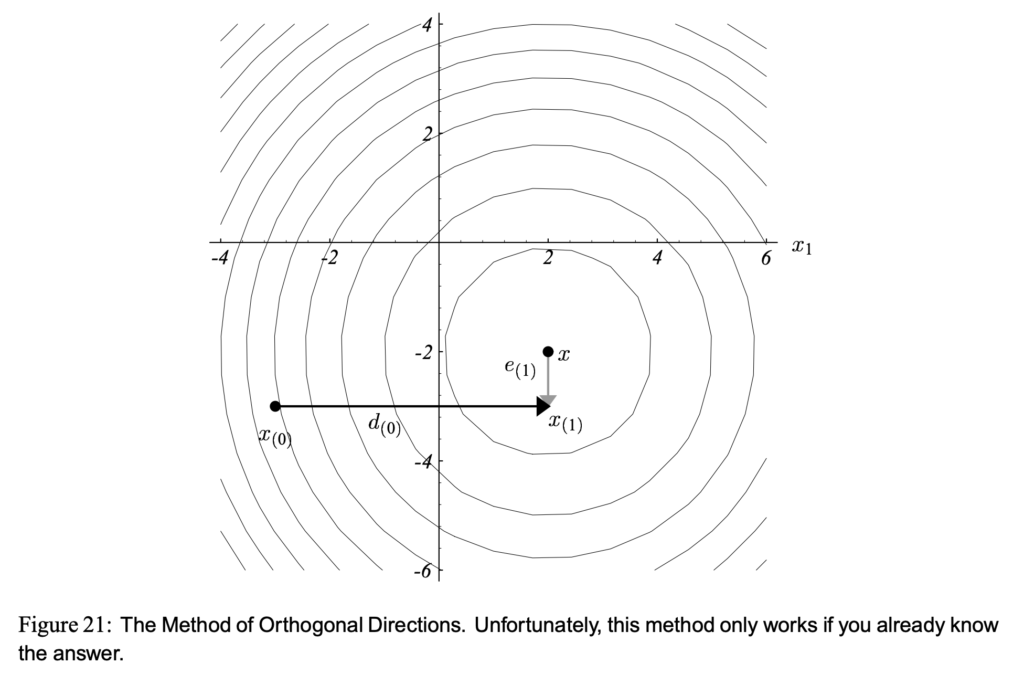
The procedure of conjugate direction methods starts from finding ![]() search directions. If
search directions. If ![]() can be orthogonal to each other, we can easily approach
can be orthogonal to each other, we can easily approach ![]() in
in ![]() steps, as in Figure 21. But theoretically we are not able to find such
steps, as in Figure 21. But theoretically we are not able to find such ![]() search directions. Instead, we can use Gram-Schmidt Conjugation and
search directions. Instead, we can use Gram-Schmidt Conjugation and ![]() linearly independent vectors to construct
linearly independent vectors to construct ![]()
![]() -orthogonal search directions. And it is provable that using
-orthogonal search directions. And it is provable that using ![]()
![]() -orthogonal search directions we can also approach
-orthogonal search directions we can also approach ![]() in
in ![]() steps. However, for arbitrary
steps. However, for arbitrary ![]() Gram-Schmidt Conjugation requires
Gram-Schmidt Conjugation requires ![]() space and
space and ![]() time complexity, which is a disadvantage in practice.
time complexity, which is a disadvantage in practice.
The method of conjugate gradients refers to the conjugate direction method when ![]() are actually residuals
are actually residuals ![]() . Fortunately, it has a nice property that space complexity and time complexity can be reduced to
. Fortunately, it has a nice property that space complexity and time complexity can be reduced to ![]() , where
, where ![]() is the number of nonzero entries of
is the number of nonzero entries of ![]() . Conjugate gradient can be summarized as follows:
. Conjugate gradient can be summarized as follows:

Once you understand TRPO, PPO is much easier to be understood. PPO just simplifies the constrained optimization in TRPO to an unconstrained optimization problem. The main objective function of PPO is:
![Rendered by QuickLaTeX.com L^{CLIP}\newline=CLIP\left(\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} A_{\pi_{\theta_{old}}}(s,a)\right]\right)\newline=CLIP\left(\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[r(\theta)A_{\pi_{\theta_{old}}}(s,a)\right]\right)\newline=\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}, a\sim \pi_{\theta_{old}}} \left[min(r(\theta), clip(r(\theta), 1-\epsilon, 1+\epsilon)) \cdot A_{\pi_{\theta_{old}}}(s,a)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-7a88ae62a682d12e908cfc57b8527b5d_l3.png)
Let’s understand this clipped objective by some example. If ![]() is positive, the model tries to increase
is positive, the model tries to increase ![]() but no more than
but no more than ![]() ; if
; if ![]() is negative, the model tries to decrease
is negative, the model tries to decrease ![]() but no less than
but no less than ![]() . This way, the change of the policy is limited.
. This way, the change of the policy is limited.
Now, let me examine the paper [5], because of which I started investigating TRPO and PPO. [5] models each joint in a robot in a locomotion task as a node in a graph. In graph learning, each node is represented as an embedding. At any given time step, the state feature can be summarized by all nodes’ embeddings. In [5], the policy network is learned through PPO.
[4] uses graph learning to model job scheduling graphs. But they use REINFORCE to learn their policy because their actions are defined as selecting one node out of all available nodes for scheduling.
Besides using graph learning to encode a graph into some feature representation, I’ve also seen people using tree-LSTM to encode tree-like graphs [14].
Reference
[1] Spinning Up doc about TRPO: https://spinningup.openai.com/en/latest/algorithms/trpo.html
[2] Trust Region Policy Optimization: https://arxiv.org/abs/1502.05477
[3] Proximal Policy Optimization Algorithms: https://arxiv.org/abs/1707.06347
[4] Learning Scheduling Algorithms for Data Processing Clusters: https://arxiv.org/abs/1810.01963
[5] NerveNet: Learning Structured Policy with Graph Neural Networks: https://openreview.net/pdf?id=S1sqHMZCb
[6] An Introduction to the Conjugate Gradient Method Without the Agonizing Pain: https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf
[7] CS294-112 10/11/17: https://www.youtube.com/watch?v=ycCtmp4hcUs&feature=youtu.be&list=PLkFD6_40KJIznC9CDbVTjAF2oyt8_VAe3
[8] Towards Data Science PPO vs. TRPO: https://towardsdatascience.com/introduction-to-various-reinforcement-learning-algorithms-part-ii-trpo-ppo-87f2c5919bb9
[9] Efficiently Computing the Fisher Vector Product in TRPO: http://www.telesens.co/2018/06/09/efficiently-computing-the-fisher-vector-product-in-trpo/
[10] TRPO (Trust Region Policy Optimization) : In depth Research Paper Review: https://www.youtube.com/watch?v=CKaN5PgkSBc
[11] Optimization Overview: https://czxttkl.com/2016/02/22/optimization-overview/
[12] https://wiseodd.github.io/techblog/2018/03/14/natural-gradient/
[14] Learning to Perform Local Rewriting for Combinatorial Optimization https://arxiv.org/abs/1810.00337