My Lempel-Ziv Compressor

Lempel-Ziv algorithm is a widely known compression algorithm. Its compression rate is proved to asymptotically reach the entropy of per symbol in the sequence to be compressed, when the length of the sequence is long enough.i.e., , where is per symbol entropy in the sequence . If, for example, you have a sequence of letters of size and each letter is encoded with 8 bits ASCII code, then the best compressed sequence also in ASCII will be of length .

More details can be found in the classic information theory book written by Thomas & Cover.

I implemented my own Lempel-Ziv compressor/decompressor below. I intentionally challenged myself to write them as short as possible (perhaps in trade of readability).

Code

compress.py

import sys
from math import *

line = sys.stdin.readline()
i, b, d, res = 0, 0, {}, ''  # current pointer, block number,
                             # lookup table, return string
while i < len(line):
    for j in xrange(i+1, len(line)+1):
        if d.get(line[i:j]) is None or j == len(line):
            b += 1
            res += '{0:0{1}b}'.format(b-d.get(line[i:j-1], b), 
                int(ceil(log(b, 2)))) + line[j-1]
            d[line[i:j]] = b
            i, j = j, len(line)  # stop for-loop for j if cond1

sys.stdout.write(res[1:])    # strip prefix for first block

decompress.py

import sys
from math import *
 
line = sys.stdin.readline()
i, b, d, res = 0, 1, {}, ''     # current pointer, block number,
                                # lookup table, return string
while i < len(line):
	r = int(ceil(log(b, 2)))    # prefix range   
	code = d.get(b-int('0'+line[i:i+r], 2), '') + line[i+r]
	d[b] = code
	res += code
	i = i + r + 1
	b += 1

sys.stdout.write(res)

Usage (helper perl scripts and other related files can be downloaded here.):

# file.in contains "jaa"
# file.out contains the compressed code of "jaa"
# file.out1 contains the decompressed string of file.out, which is exactly "jaa".
# 0010100111000100101001111000110011000001
perl preCompress.pl < file.in | python compress.py | perl postCompress.pl > file.out
perl preDecompress.pl < file.out | python decompress.py | perl postDecompress.pl > file.out1

# Encode and decode my own name
echo -n 'zhc' | perl preCompress.pl | python compress.py | python decompress.py | perl postDecompress.pl

# Encode and decode random string
echo -n 'zasdfasdfasdlfasdlhc' | perl preCompress.pl | python compress.py | python decompress.py | perl postDecompress.pl

# Encode and decode files
perl preCompress.pl < alice.txt | python compress.py | perl postCompress.pl > alice.out
perl preDecompress.pl < alice.out | python decompress.py | perl postDecompress.pl > alice.out1

# Decode "CS6800"
echo -n 00110001101100011011100100111101110001010010011001100100011100100000000 | python decompress.py | perl postDecompress.pl

# Generate long sequence according to a markov chain (only three symbols)
python gen_mc.py > mc.in
# Compress long sequence generated according to markov chain
perl preCompress.pl < mc.in | python compress.py | perl postCompress.pl > mc_compressed.out
perl preDecompress.pl < mc_compressed.out | python decompress.py | perl postDecompress.pl > mc_decompressed.out1

Some observation

1. The higher the per symbol entropy of the sequence is, the poorer the compression algorithm performs. I compressed a sequence containing only three symbols with around 30% compression rates. (The entropy per symbol is 1.459 bits/symbol) I also compressed a sequence of text (containing 26 English letters) from Alice Wonderland but with only 84% compression rate. As we know, the entropy of English letter should be much higher than 1.459 bits/symbol.
2. I used real compressor such as `gzip` to compress my three symbol sequence, the compression rate is around 23%. As we know from the proved theory, the compression rate cannot be less than .
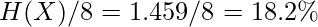