Leetcode 188: Best Time to Buy and Sell Stock IV

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/

 

Code

class Solution(object):
    def maxProfit(self, k, prices):
        """
        :type k: int
        :type prices: List[int]
        :rtype: int
        """
        if not prices or not k:
            return 0
        if k >= len(prices)/2:
            profit = 0
            for i in xrange(1, len(prices)):
                if prices[i] - prices[i-1] > 0:
                    profit += prices[i] - prices[i-1]
            return profit

        profit = [[0] * len(prices) for _ in xrange(k+1)]        
        for i in xrange(1, k+1):
            tmp = -prices[0]
            for j in xrange(1, len(prices)):
                profit[i][j] = max(profit[i][j-1], tmp + prices[j])
                tmp = max(tmp, profit[i-1][j-1] - prices[j])
        
        return profit[-1][-1]
        

 

Idea

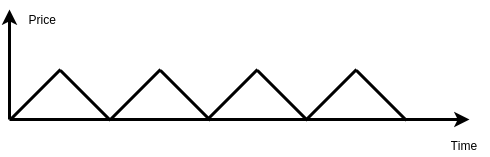
First of all, let’s deal with the case where `k >= len(prices)/2`. In this case, you can use at most `k` transactions to get profits in all ascending intervals of prices. You can imagine an extreme case where the prices go like this:

In this extreme case, the number of ascending intervals is never going to be larger than `len(prices)/2`. So is the number of transactions needed to capture all ascending intervals.

For more smooth cases, you don’t need `len(prices)/2` that many transactions to get all ascending intervals. However, we can use the same piece of codes to deal with any cases, as long as `k >= len(prices)/2`.  (line 10 – 15)

Now let’s look at the core part. I use a 2D array `profit` to capture the temporary maximum profit I can get: `profit[i][j]` is the maximum profit you can get by using `i` transactions and the first `j` prices. There is also a variable `tmp`. Its value is the maximum money left in the pocket after you buy the stock but haven’t sold it before you process `profit[i][j]`.  You can imagine `tmp` as the current best buy point.

 

Reference

https://leetcode.com/discuss/25603/a-concise-dp-solution-in-java