In this post, we dig into more details of Direct Preference Optimization [1], a popular method used in RLHF.
First, we start from the normal RLHF objective that is typically used in PPO literature, which is equation 3 in the DPO paper [1]. Typically, we have input prompts ![]() and an LLM’s responses
and an LLM’s responses ![]() . The objective of optimizing the LLM,
. The objective of optimizing the LLM, ![]() , is:
, is:
![]()
which states that we want to maximize the reward model score ![]() but also, in balance, to minimize the KL-divergence from a reference policy
but also, in balance, to minimize the KL-divergence from a reference policy ![]() .
.
The equation above can be rewritten by incorporating the KL-divergence term into the reward function. Because ![]() , we have
, we have
![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) - \beta (\log \pi_\theta(y|x) - \log \pi_{ref}(y|x)) \right] \newline = \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) + \beta \log \pi_{ref}(y|x) - \beta \log \pi_\theta(y|x) \right] \newline \text{because }-\log \pi_\theta(y|x) \text{ is an unbiased estimator of entropy } \mathcal{H}(\pi_\theta)=-\sum_y \pi_\theta(y|x) \log \pi_\theta(y|x), \newline \text{we can transform to equation 2 in [3]} \newline= \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) + \beta \log \pi_{ref}(y|x) + \beta \mathcal{H}(\pi_\theta)\right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-a33dea15a8c89bf3260776df1cf4d7be_l3.png)
Now there are two perspectives for how to solve the maximization problem above. The first solution is based on the DPO paper’s Appendix A.1 [1]:
![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[r_\phi(x,y) - \beta (\log \pi_\theta(y|x) - \log \pi_{ref}(y|x)) \right] \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} - \frac{1}{\beta}r_\phi(x,y) \right] \newline =\min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} - \log exp\left(\frac{1}{\beta}r_\phi(x,y)\right) \right] \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right)} \right] \newline \pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right) \text{ may not be a valid distribution. But we can define a valid distribution:} \pi^*(y|x)=\frac{1}{Z(x)}\pi_{ref}(y|x)exp\left(\frac{1}{\beta}r_\phi(x,y)\right), \text{ where } Z(x) \text{ is a partition function not depending on } y \newline = \min_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)} \left[ \log \frac{\pi_\theta(y|x)}{\pi^*(y|x)} \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-abe10cca2808da4aaf2d3f96b11abd12_l3.png)
Due to the so-called Gibbs’ inequality, the optimal solution is when ![]() everywhere.
everywhere.
The second solution is based on Maximum Entropy RL [6] and can be solved by the method of Lagrangian multipliers. The constrained objective function from what we derived above is:
![Rendered by QuickLaTeX.com \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y\sim \pi_\theta(y|x)}\left[\underbrace{r_\phi(x,y) + \beta \log \pi_{ref}(y|x)}_{\text{actual reward function}} + \beta \mathcal{H}(\pi_\theta)\right] \newline s.t. \quad \sum\limits_y \pi_\theta(y|x)=1,](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-806a96f47b9f83798b88f60131252bf1_l3.png)
which is exactly the objective function of MaxEnt RL with the actual reward as ![]() . Note, we are solving a one-step MaxEnt RL problem. So we can use the Lagrangian multipliers method to reach the same solution. See 1hr:09min in [5] for more details.
. Note, we are solving a one-step MaxEnt RL problem. So we can use the Lagrangian multipliers method to reach the same solution. See 1hr:09min in [5] for more details.

Now we have introduced two ways to derive the optimal solution of ![]() . With some arrangement, we can see that this formula entails that the reward function can be represented as a function of
. With some arrangement, we can see that this formula entails that the reward function can be represented as a function of ![]() and
and ![]() :
:
![]()
With collected human preference data ![]() and a Bradley-Terry model, we know that
and a Bradley-Terry model, we know that ![]()
We can convert ![]() into the logit [7]:
into the logit [7]:![]()
which can be solved by maximum likelihood as in logistic regression:![Rendered by QuickLaTeX.com -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[\log \sigma \left(r(x, y_w) - r(x, y_l)\right) \right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \left(\beta \log \pi^*_\theta(y_w|x) - \beta \log \pi_{ref} (y_w | x) \right) - \left( \beta \log \pi^*_\theta(y_l |x) - \beta \log \pi_{ref} (y_l | x) \right)\right)\right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \beta \log \frac{\pi^*_\theta(y_w|x)}{\pi_{ref} (y_w | x)} - \beta \log \frac{\pi^*_\theta(y_l |x)}{\pi_{ref} (y_l | x)} \right) \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-f305d09d3d4969371cc4d16552d0e9fe_l3.png)
We have been deriving the optimal DPO solution assuming the environment is a one-step MDP (i.e., bandits) because we only receive a reward for an entire response. However, if we have dense rewards on each token, the decoding process is essentially a token-level MDP, where decoding each token is one step in the MDP. The Bradley-Terry model in the token-level MDP becomes: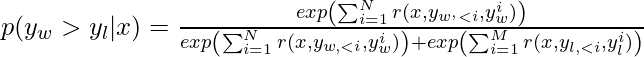
In such a case, does the DPO loss function, ![]() , still align the underlying policy to the Bradley-Terry preference probability defined in the token-level MDP? The answer is yes as proved in [3]. We first need to make an interesting connection between the decoding process and multi-step Maximum Entropy RL. (Note, earlier in this post, we have made a connection between on-step Maximum Entropy RL and DPO in the setting of bandits.)
, still align the underlying policy to the Bradley-Terry preference probability defined in the token-level MDP? The answer is yes as proved in [3]. We first need to make an interesting connection between the decoding process and multi-step Maximum Entropy RL. (Note, earlier in this post, we have made a connection between on-step Maximum Entropy RL and DPO in the setting of bandits.)
In multi-step Maximum Entropy RL [6], the objective is ![]() . People have proved the optimal policy can be derived as
. People have proved the optimal policy can be derived as ![]() where
where ![]() and
and ![]() are the corresponding Q-function and V-function in the MaxEnt RL [8]. For any LLM, its decoding policy
are the corresponding Q-function and V-function in the MaxEnt RL [8]. For any LLM, its decoding policy ![]() is a softmax over the whole vocabulary. Therefore,
is a softmax over the whole vocabulary. Therefore, ![]() can be seen as an optimal policy of a MaxEnt RL in a token-level MDP with a particular reward function (however the reward function is unknown to us).
can be seen as an optimal policy of a MaxEnt RL in a token-level MDP with a particular reward function (however the reward function is unknown to us).
Based on the definition of Q functions and V functions (with a discount factor equal to 1), we have ![]() in terms of an LLM’s decoding process. We could re-arrange the formula to represent per-token reward as:
in terms of an LLM’s decoding process. We could re-arrange the formula to represent per-token reward as: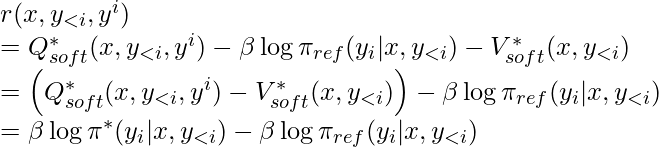
The logit of the Bradley-Terry model under the token-level MDP is then: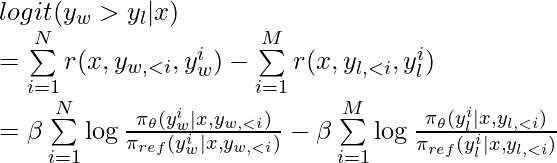
By learning this logit using maximum likelihood, we reach the same loss function as we derive in the bandits setting:![Rendered by QuickLaTeX.com -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left(\beta \sum\limits_{i=1}^{N}\log \frac{\pi_\theta(y_w^i | x, y_{w, <i})}{\pi_{ref}(y_w^i | x, y_{w,<i})} - \beta \sum\limits_{i=1}^M \log \frac{\pi_\theta(y_l^i | x, y_{l, <i})}{\pi_{ref}(y_l^i | x, y_{l,<i})} \right) \right] \newline = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[ \log \sigma \left( \beta \log \frac{\pi^*_\theta(y_w|x)}{\pi_{ref} (y_w | x)} - \beta \log \frac{\pi^*_\theta(y_l |x)}{\pi_{ref} (y_l | x)} \right) \right]](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-982b48b23d236150e21ff1c8f0e9f051_l3.png)
A few notes to conclude this post:
- Adding a KL divergence penalty in tandem with reward model scores seems to be just one option of telling the LLM to not deviate much from the reference policy. In theory, there could be other regularizers (e.g., L2 norm). But, surprisingly, using KL divergence penalty makes very interesting connection to Maximum Entropy RL and thus provides many theoretical groundings for DPO.
- In practice, our preference data is collected once in advance using a mix of previous policies. In other words, preference data does not come from the LLM policy being updated. So in practice DPO is in fact an off-policy algorithm and data efficiency may not be optimal. (Note, if we have infinite diverse preference data not coming from the incumbent DPO policy, DPO may still converge to the optimal policy, just that the data efficiency is not optimal.) People have since proposed methods to generate more on-policy preference data: [9, 10, 11]
Reference
- Direct Preference Optimization: Your Language Model is Secretly a Reward Model: https://arxiv.org/abs/2305.18290
- Reinfocement Learning in LLMs: https://czxttkl.com/2024/01/23/reinfocement-learning-in-llms/
- From r to Q∗: Your Language Model is Secretly a Q-Function: https://arxiv.org/abs/2404.12358
- Controlled decoding from language models: https://arxiv.org/abs/2310.17022
- L1 MDPs, Exact Solution Methods, Max-ent RL (Foundations of Deep RL Series): https://www.youtube.com/watch?v=2GwBez0D20A
- Reinforcement Learning with Deep Energy-Based Policies: https://arxiv.org/pdf/1702.08165
- https://en.wikipedia.org/wiki/Bradley%E2%80%93Terry_model#Definition
- http://www.lamda.nju.edu.cn/yanggy/slide/Maximum_entropy_RL_Guoyu_Yang.pdf
- Direct Language Model Alignment from Online AI Feedback: https://arxiv.org/abs/2402.04792
- Statistical Rejection Sampling Improves Preference Optimization: https://arxiv.org/abs/2309.06657
- Some things are more CRINGE than others: Iterative Preference Optimization with the Pairwise Cringe Loss: https://arxiv.org/abs/2312.16682