Leetcode 99: Recover Binary Search Tree

https://leetcode.com/problems/recover-binary-search-tree/

Recover Binary Search Tree

Total Accepted: 41308 Total Submissions: 166942 Difficulty: Hard

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Note:
A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

confused what "{1,#,2,3}" means? > read more on how binary tree is serialized on OJ.

OJ’s Binary Tree Serialization:

The serialization of a binary tree follows a level order traversal, where ‘#’ signifies a path terminator where no node exists below.

Here’s an example:

The above binary tree is serialized as "{1,2,3,#,#,4,#,#,5}".

Code

import sys
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def __init__(self):
        self.prev = TreeNode(-sys.maxint)
        
    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: void Do not return anything, modify root in-place instead.
        """
        brk_nodes = []
        self.inorder(root, brk_nodes)
            
        brk_nodes[0].val, brk_nodes[1].val = brk_nodes[1].val, brk_nodes[0].val
        
        
    def inorder(self, root, brk_nodes):
        def add_to_brk(prev):
            if len(brk_nodes)==0:
                brk_nodes.append(prev)
                brk_nodes.append(root)
            else:
                brk_nodes[1] = root
                    
        # traverse left            
        if root.left:
            self.inorder(root.left, brk_nodes)
            
        if self.prev.val > root.val:
            add_to_brk(self.prev)
        
        self.prev = root
        
        # traverse right
        if root.right:
            self.inorder(root.right, brk_nodes)

Idea

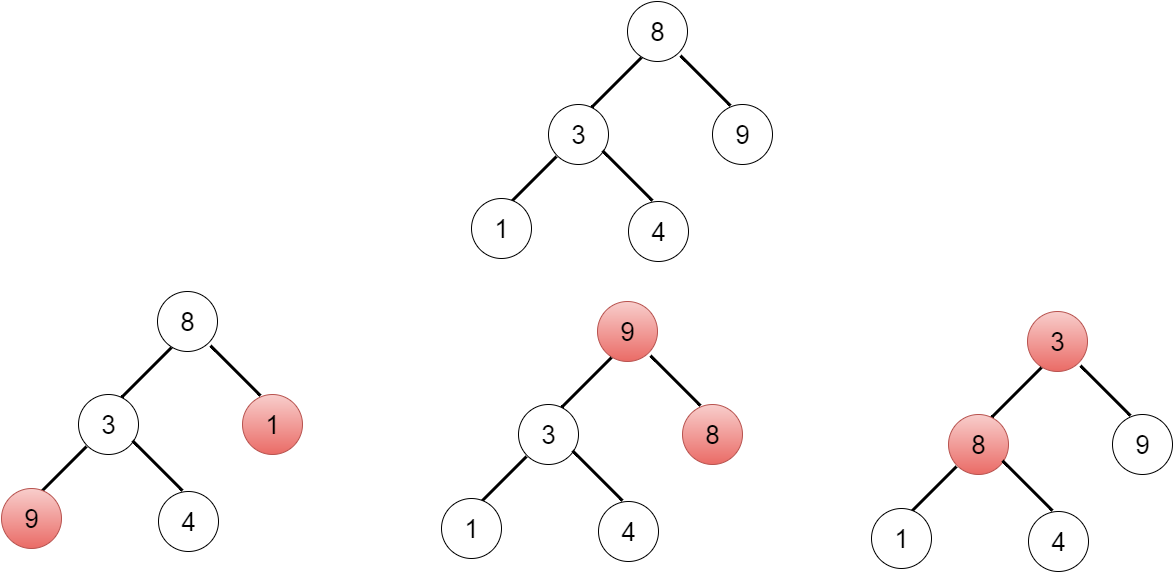
We use the property that if a BST is valid, its inorder traversal will return the data in ascending order. For example, the top tree in the following plot is a valid binary search tree. Therefore, its inorder traversal should return 13489. All elements are larger than their previous elements.

The three trees on the bottom are all invalid binary search trees, each with exactly two nodes exchanged (marked as red). You may recognize that an inorder traversal of an invalid BST has at most two places where an element is smaller than the element right before it. More specifically:

The bottom left tree: inorder traversal is 93481. 3 is smaller than 9. 1 is smaller than 8.

The bottom middle tree: inorder traversal is 13498. 8 is smaller than 9.

The bottom right tree: inorder traversal is 18439. 4 is smaller than 8. 3 is smaller than 4.

Using this rule, we implement our code whenever we find previous visited node has larger value than the current node’s value. Whenever we find such node and the current broken node list is empty, we add the previous element and the current element together, although the current element may or may not be the broken node. (Line 27-28) But writing in this way will help us deal with the cases when the inorder traversal only contains one misplacement of number (e.g., the bottom middle tree in the plot).

Since we at most call O(N) recursive calls of `self.inorder()` function, the space complexity is O(N). The time complexity is O(N) because in the worst case you need to traverse all elements before you determine the two broken nodes.

Reference

The same idea applied in this post: https://leetcode.com/discuss/13034/no-fancy-algorithm-just-simple-and-powerful-order-traversal
This problem which is more space efficient: https://leetcode.com/discuss/26310/detail-explain-about-morris-traversal-finds-incorrect-pointer

Leetcode 99: Recover Binary Search Tree

Recover Binary Search Tree

Leave a comment

Cancel reply