In this post, let’s visit how modern LLMs encode positional information. We start from the most famous paper in this domain [1] and dive into some key details.
Why we need positional encoding
LLMs need positional encodings to differentiate different semantic meanings of the same word. We use the motivational example from [2]:

The two “dogs” refer to different entities. Without any positional information, the output of a (multi headed) self attention operation is identical for the same token in different positions.
Preliminaries
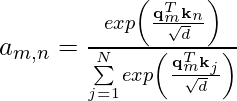
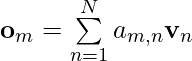
Sinusoidal Absolute Position Encoding
One drawback of using the additive sinusoidal PE is that ![]() makes
makes ![]() a bit chaotic. In the motivational example from [4], suppose
a bit chaotic. In the motivational example from [4], suppose ![]() , then at different positions 0 ~ 7,
, then at different positions 0 ~ 7, ![]() can become any value around
can become any value around ![]() , making LLMs hard to generalize.
, making LLMs hard to generalize.

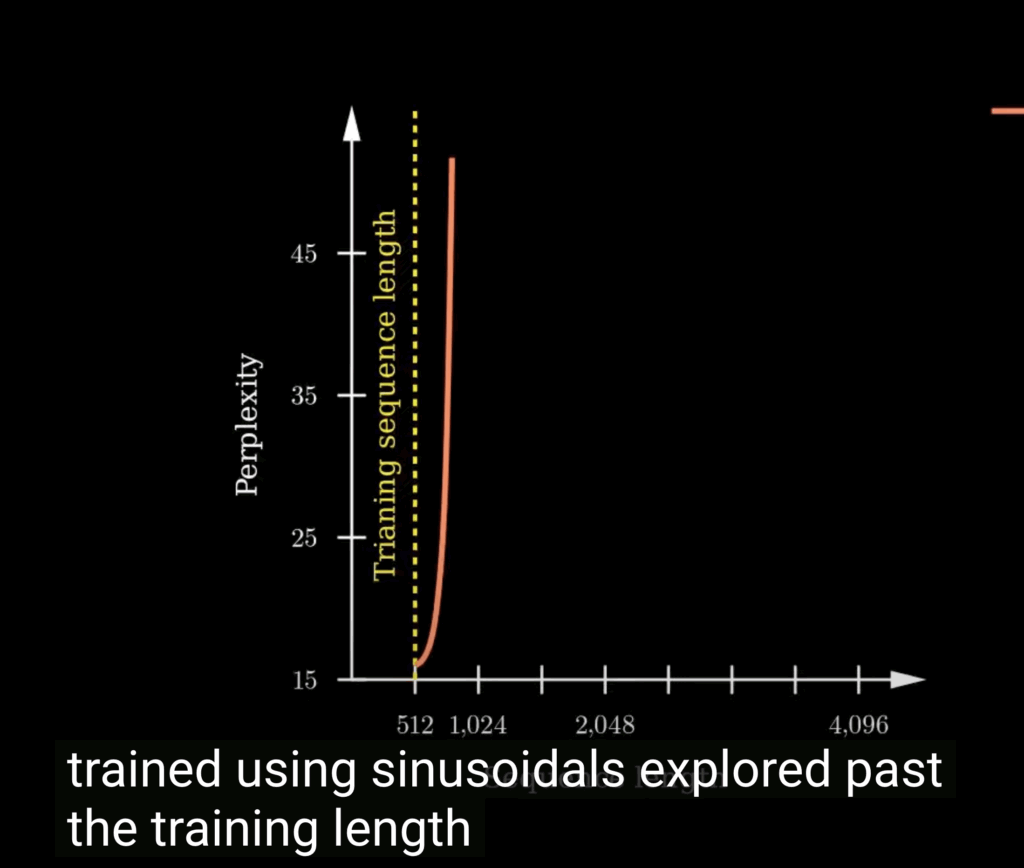
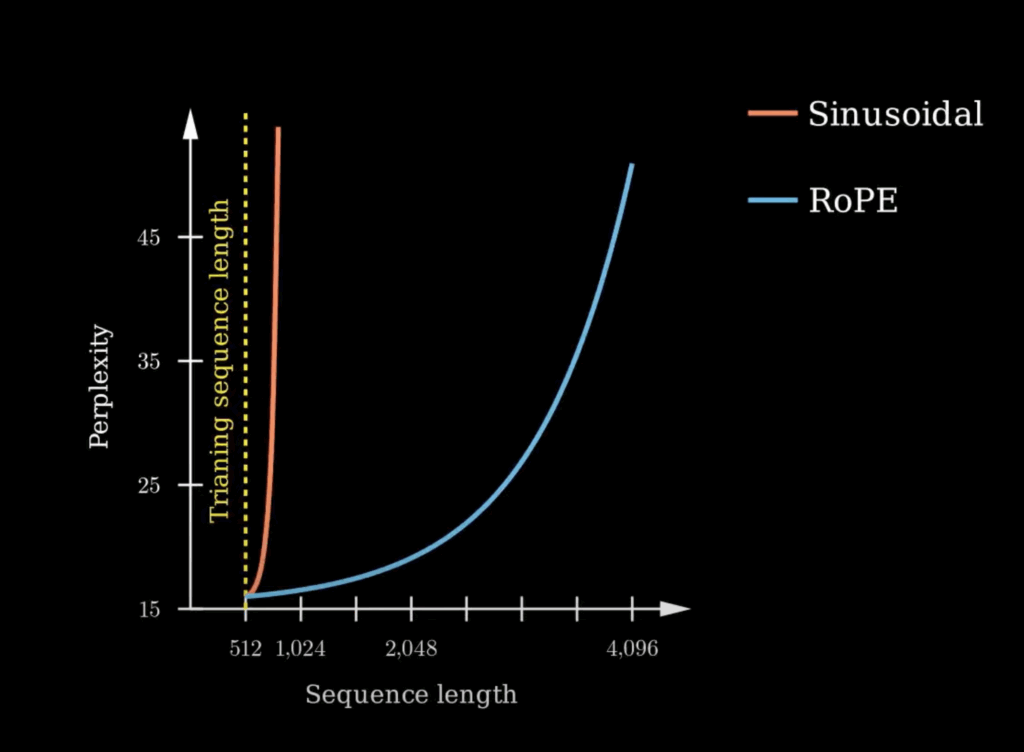
Research has shown that the perplexity of the models trained with sinusoidal absolute position embeddings exploded past the training length.
RoPE (Rotary Positional Embeddings)
RoPE uses a multiplication form for positional embeddings. As we know, multiplying a vector with a matrix is equivalent to rotate that vector by some angle.
![]()
![]()
![]()
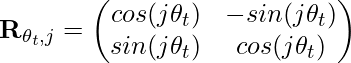
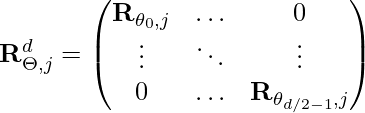
![]()
![]() by default
by default
(Some clarification about the notation: in ![]() ,
, ![]() is the symbol for the imaginary dimension,
is the symbol for the imaginary dimension, ![]() is the position in the sequence.
is the position in the sequence. ![]() is the dimension index of embeddings hence
is the dimension index of embeddings hence ![]() )
)
As we can see, with RoPE now the transformed vectors are nicely rotated as the position changes. And its context window extrapolation performance is much better than the sinusoidal positional embeddings.

RoPE has many desired properties of ideal positional embeddings. For any two positions ![]() and
and ![]() , their (unnormalized) attention scores depend on the position difference
, their (unnormalized) attention scores depend on the position difference ![]() . As
. As ![]() increases, the attention scores will decrease (if everything else was kept the same), which is proved Section 3.4.3 in [1].
increases, the attention scores will decrease (if everything else was kept the same), which is proved Section 3.4.3 in [1].
![Rendered by QuickLaTeX.com \mathbf{q}_t^T \mathbf{k}_s = \left(\mathbf{R}^{d}_{\Theta, t} \mathbf{W}_q \mathbf{x}_t \right)^T \left(\mathbf{R}^{d}_{\Theta, s} \mathbf{W}_k \mathbf{x}_s \right) \newline\qquad =\mathbf{x}^T_t \mathbf{W}_q \mathbf{R}^{d}_{\Theta, t-s} \mathbf{W}_k \mathbf{x}_s \newline\qquad = Re\left[\sum\limits_{i=0}^{d/2-1} \mathbf{q}_{[2i:2i+1]} \mathbf{k}^*_{[2i:2i+1]} e^{i(t-s)\theta_{i}} \right]\newline \qquad \text{decrease as t-s increases}](https://czxttkl.com/wp-content/ql-cache/quicklatex.com-d94c4f09c13f52eb6323ff2ef3d152a1_l3.png)
How to choose RoPE base
In practice, we often face situations where we pre-train a model with a context window ![]() , post-train a context window
, post-train a context window ![]() , and need to inference with a longer context window
, and need to inference with a longer context window ![]() . We assume
. We assume ![]() . Without any remedies, perplexity will shoot up outside
. Without any remedies, perplexity will shoot up outside ![]() (even though RoPE is already better than Sinusoidal). [11] shows that we can improve the extrapolation ability of RoPE by either increasing/decreasing the base and post-training on longer context lengths.
(even though RoPE is already better than Sinusoidal). [11] shows that we can improve the extrapolation ability of RoPE by either increasing/decreasing the base and post-training on longer context lengths.
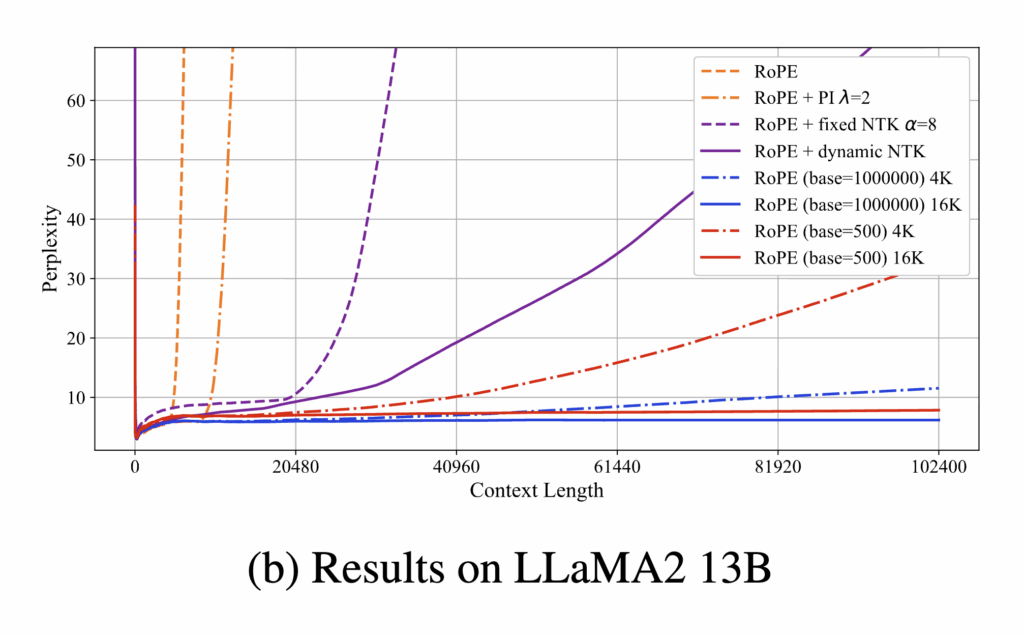
In Figure 1.b, they showed that, for Llama2 13b with ![]() and
and ![]() , post-training RoPE with
, post-training RoPE with ![]() and
and ![]() has the best extrapolation performance, followed by
has the best extrapolation performance, followed by ![]() and
and ![]() , then followed by
, then followed by ![]() and
and ![]() , and finally
, and finally ![]() and
and ![]() :
:
Let us first explain why decreasing ![]() can improve extrapolation. As we introduced, when computing attention scores, RoPE is essentially rotating embeddings by different angles – for any two positions
can improve extrapolation. As we introduced, when computing attention scores, RoPE is essentially rotating embeddings by different angles – for any two positions ![]() and
and ![]() in the sequence, it rotates embeddings with
in the sequence, it rotates embeddings with ![]() , where
, where ![]() ,
, ![]() . The larger the base
. The larger the base ![]() is, the smaller rotation angel it will be. Rotations have periods, meaning that after a certain amount of rotation, rotated embeddings will be at the same position as its original position without rotation. Just like trigonometric functions (cosine and sine) [12], periods of RoPE are determined by
is, the smaller rotation angel it will be. Rotations have periods, meaning that after a certain amount of rotation, rotated embeddings will be at the same position as its original position without rotation. Just like trigonometric functions (cosine and sine) [12], periods of RoPE are determined by ![]() ,
, ![]() . So you can see that for some dimensions periods are shorter while some dimensions have longer periods, all depending on what
. So you can see that for some dimensions periods are shorter while some dimensions have longer periods, all depending on what ![]() is.
is.
To have minimal extrapolation error, we should have ![]() so that the model has learned representation for every possible relative position difference
so that the model has learned representation for every possible relative position difference ![]() that could occur during testing. However, if we can’t do that (i.e.,
that could occur during testing. However, if we can’t do that (i.e., ![]() ), the best compromise we can make in post-training is to let as many embedding dimensions as possible to have small periods (
), the best compromise we can make in post-training is to let as many embedding dimensions as possible to have small periods (![]() ). As such, the model will see full cycles of rotations of those dimensions within
). As such, the model will see full cycles of rotations of those dimensions within ![]() , learn better understanding/representation of rotations, and has better chance to extrapolate well in a longer context length.
, learn better understanding/representation of rotations, and has better chance to extrapolate well in a longer context length.
Let’s use some example. In Llama2, the total dimension of embeddings is 128, ![]() ,
, ![]() . This means that when
. This means that when ![]() ,
, ![]() . Therefore, there will be 92 dimensions whose periods can fit into the 4k context length while the remaining 36 dimensions’ periods are longer than 4k. If we change
. Therefore, there will be 92 dimensions whose periods can fit into the 4k context length while the remaining 36 dimensions’ periods are longer than 4k. If we change ![]() to 500, then every dimension’s period will fit in the 4k context length. That’s why [11] found that
to 500, then every dimension’s period will fit in the 4k context length. That’s why [11] found that ![]() can lead to good extrapolation performance.
can lead to good extrapolation performance.
Now we explain why increasing ![]() can also help extrapolation. Increasing
can also help extrapolation. Increasing ![]() in post-training means rotation speed is smaller (i.e.,
in post-training means rotation speed is smaller (i.e., ![]() decreases) and period is longer (i.e.,
decreases) and period is longer (i.e., ![]() increases). Therefore, in test time, even we see a relative position difference
increases). Therefore, in test time, even we see a relative position difference ![]() which is larger than
which is larger than ![]() , the rotation pattern
, the rotation pattern ![]() may still be seen before in pre-training or post-training. The role of post-training with an increased
may still be seen before in pre-training or post-training. The role of post-training with an increased ![]() is to bridge the model’s understanding between the rotation pattern observed in pre-training / post-training and the rotation pattern that could be observed in test-time. Increasing
is to bridge the model’s understanding between the rotation pattern observed in pre-training / post-training and the rotation pattern that could be observed in test-time. Increasing ![]() in RoPE is used in well-cited research [13, 14]. In this vein, another technique (Position Interpolation from [10]) is similar – they try to scale large rotation
in RoPE is used in well-cited research [13, 14]. In this vein, another technique (Position Interpolation from [10]) is similar – they try to scale large rotation ![]() that could happen in large
that could happen in large ![]() down to something that is already learned in post-training.
down to something that is already learned in post-training.

Advanced Topics
- The NoPE paper claims that we do not even need explicit positional encodings [16]. Whether it can become a mainstream remains to be seen [17].
- Extending to infinite context requires us to have some memory mechanism. [15] proposes one mechanism, in which we first chunk a sequence into N segments. Within each segment, attention is computed with an additional compressive memory matrix. The compressive memory matrix (
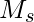 ) contains compressed information from all previous segments and is updated after each segment to carry new information over. Therefore, in theory, the model can extend to infinite context.
) contains compressed information from all previous segments and is updated after each segment to carry new information over. Therefore, in theory, the model can extend to infinite context.
Reference
[1] ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING: https://arxiv.org/pdf/2104.09864
[2] https://huggingface.co/blog/designing-positional-encoding
[3] https://www.gradient.ai/blog/scaling-rotational-embeddings-for-long-context-language-models
[4] https://www.youtube.com/watch?v=GQPOtyITy54
[5] https://cedricchee.com/blog/rope_embeddings/
[6] https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html
[7] The Impact of Positional Encoding on Length Generalization in Transformers: https://arxiv.org/pdf/2305.19466
[8] https://czxttkl.com/2018/10/07/eulers-formula/
[9] https://www.youtube.com/watch?v=C6rV8BsrrCc
[10] Extending context window of large language models via positional interpolation
[11] Scaling Laws of RoPE-based Extrapolation
[13] Effective Long-Context Scaling of Foundation Models: https://arxiv.org/abs/2309.16039
[14] Code Llama: https://ai.meta.com/research/publications/code-llama-open-foundation-models-for-code/
[15] Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention: https://arxiv.org/abs/2404.07143
[16] The Impact of Positional Encoding on Length Generalization in Transformers: https://arxiv.org/abs/2305.19466