How does Metropolis-Hastings algorithm work?

I learned about Markov Chain Monte Carlo (MCMC) algorithm a little bit during my phd but I did not record my thoughts back then. In this post, I revisit the core concept of MCMC, particularly focusing on illustrating the Metropolis-Hastings (MH) algorithm.

What is the motivation of MCMC?

Suppose you have observed some data $x$ . You would like to express the distribution of $x$ as some distribution which is parameterized by $\theta$ . You have some prior $p(\theta)$ . You would like to know the distribution of the posterior distribution $p(\theta|x)$ . Based on Bayes’ theorem,

$p(\theta|x)=\frac{p(\theta) p(x|\theta)}{p(x)}=\frac{p(\theta) p(x|\theta)}{\int_\theta p(\theta) p(x|\theta) d\theta}$

The denominator $\int_\theta p(\theta) p(x|\theta) d\theta$ is often hard to compute. Therefore, it is hard to know the exact statistics of the posterior distribution, such as the mean of the posterior distribution. MCMC has some mechanism to allow you sample points on the space of $\theta$ such that when a sufficient amount of points of $\theta$ is sampled, they approximate the true posterior distribution $p(\theta|x)$ hence you will be able to compute the empirical statistics such as the empirical mean.

Let’s use one concrete example (taken reference from [2]). You are a teacher who wants to know the score distribution of your students. You assume the score distribution is Normal distribution $\mathcal{N}(\mu, \sigma^2)$ while $\sigma^2=4^2=16$ is a fixed variance. According to basic conjugate prior mathematics [4], you have a prior distribution $p(\mu|\mu_0, \sigma_0^2) = \mathcal{N}(\mu_0, \sigma_0^2)$ which is also a Normal distribution. You have observed 3 students’ scores therefore you can express the likelihood function as: $p(x_1, x_2, x_3|\mu, \sigma^2) \propto \frac{1}{\sigma^n} exp\left( -\frac{1}{2\sigma^2}\sum\limits_{i=1}^3 (x_i - \mu)^2 \right)$ . 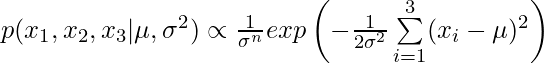In this simple example, there is an analytical expression for the posterior distribution $p(\mu| x_1, x_2, x_3)$ which is also a Normal distribution. But for our pedagogical purpose, let’s assume the posterior distribution $p(\mu|x_1, x_2, x_3)$ is impossible to compute and we have to use MCMC to infer posterior statistics such as the posterior mean.

How MCMC works? (specifically MH algorithm)

We focus on the MH algorithm, which basically has a loop of sampling a number of $\theta$ for estimating the posterior distribution. The following steps are adapted from [2]:

Begin with a plausible starting value; Let’s say you guess 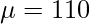$\mu=110$ at first.
Generate a new proposal by taking the last sample (110) and adding some random noise. This random noise is generated from a proposal distribution, which should be symmetric and centered on zero. In our example we will use a proposal distribution that is normal with zero mean and standard deviation of 5. This means the new proposal is 110 (the last sample) plus a random sample from N(0,5). Suppose this results in a proposal of 108.
Note that, if the proposal distribution is not symmetric, the following sample acceptance criteria (step 4&5) will need to be adjusted. See how $g(\cdot)$ is defined in [1].
Compare the likelihood value of the new proposal (i.e., 108) against the likelihood value of the posterior at the most recent sample (i.e., 110). In other words, you will compare 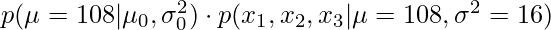$p(\mu=108|\mu_0, \sigma_0^2) \cdot p(x_1, x_2, x_3|\mu=108, \sigma^2=16)$ and $p(\mu=110|\mu_0, \sigma_0^2) \cdot p(x_1, x_2, x_3|\mu=110, \sigma^2=16)$ .
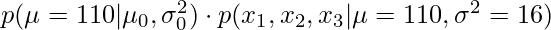Note: in many other online tutorials such as [2] and [5], people also interchangeably say that we compare the posterior value of the new proposal and the most recent sample. Since the likelihood value has only a multiplicative constant difference than the posterior, comparing the likelihood value is equivalent to comparing the posterior.
If the new proposal has a higher likelihood value than the most recent sample, then accept the new proposal.
If the new proposal has a lower likelihood value than the most recent sample, then randomly choose to accept or reject the new proposal, with a probability equal to the ratio of the two likelihood values. For example, if the likelihood value at the new proposal value is one-fifth as high as the likelihood of the most recent sample, then accept the new proposal with 20% probability.
If the new proposal is accepted, it becomes the next sample in the MCMC chain, otherwise the next sample in the MCMC chain is just a copy of the most recent sample.
This completes one iteration of MCMC. The next iteration is completed by returning to step 2.
Stop when there are enough samples (e.g., 500). Deciding when one has enough samples is a separate issue. Now you can compute any empirical statistics as you like, such as the empirical posterior mean.

The above 8 steps illustrates the core formula of MH, the acceptance criterion function [1, 3]:

$\alpha(\theta^{new}, \theta^{old})=min \left(1, \frac{p(\theta^{old}|x)g(\theta^{new}|\theta^{old})}{p(\theta^{new}|x) g(\theta^{old}|\theta^{new})}\right)$