Euler’s formula states that ![]() . When
. When ![]() , the formula becomes
, the formula becomes ![]() known as Euler’s identity.
known as Euler’s identity.
An easy derivation of Euler’s formula is given in [3] and [5]. According to Maclaurin series (a special case of taylor expansion ![]() when
when ![]() ),
),
![]()
Therefore, replacing ![]() with
with ![]() , we have
, we have
![]()
By Maclaurin series, we also have
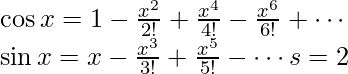
Therefore, we can rewrite ![]() as
as ![]()
Intuitive understanding of ![]() is illustrated in [1] together with its own video [4], as well as in 3Blue1Brown’s two videos [6][7].
is illustrated in [1] together with its own video [4], as well as in 3Blue1Brown’s two videos [6][7].
First, from a conventional view of coordinate system, ![]() means a point with x coordinate
means a point with x coordinate ![]() and y coordinate
and y coordinate ![]() on a unit circle (centered at the origin with radius 1) in the complex plane.
on a unit circle (centered at the origin with radius 1) in the complex plane.
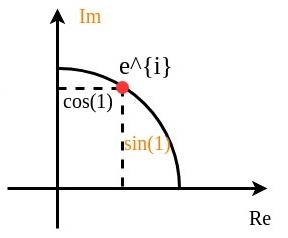
Another view is that ![]() describes the point that moves distance
describes the point that moves distance ![]() from (1,0) along the circumference of the unit circle.
from (1,0) along the circumference of the unit circle.
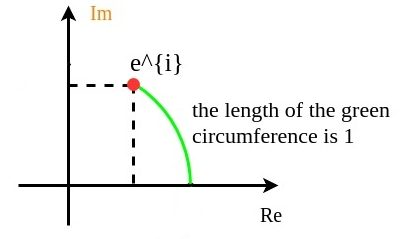
The last view, which is similar to the second view, is that ![]() specifies the point such that the degree between the x axis and the line connects that point to the origin is radiant x .
specifies the point such that the degree between the x axis and the line connects that point to the origin is radiant x .
For example, ![]() viewed in x&y coordinates:
viewed in x&y coordinates:
or viewed from the moving perspective:
or viewed from the radiant perspective:
As pointed out by [1], we can think of normal exponential as stretching an axis such that number 1 is stretched to a point denoting the exponential result. For example, ![]() means 1 is stretched to 8, or 1 is stretched to 2 first, then that point is stretched to 4, then finally that point is stretched to 8. However, complex exponential
means 1 is stretched to 8, or 1 is stretched to 2 first, then that point is stretched to 4, then finally that point is stretched to 8. However, complex exponential ![]() means to rotate from the point (1,0) at a constant rotation speed
means to rotate from the point (1,0) at a constant rotation speed ![]() . Therefore, Euler’s identity can be interpreted as starting from point (1,0), a point moves half of the circle (radiant
. Therefore, Euler’s identity can be interpreted as starting from point (1,0), a point moves half of the circle (radiant ![]() ) and ends up at (-1, 0), therefore
) and ends up at (-1, 0), therefore ![]() . A good diagram summarizing this intuition is as below:
. A good diagram summarizing this intuition is as below:
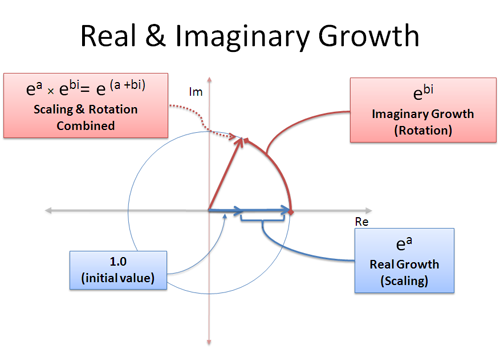
Why understanding Euler’s formula as a point rotating on a unit circle helps? One example in which Euler’s formula is useful is Fourier transform. The goal of Fourier transform is to turning signals measured in time space into analyzable, frequency-based spectrum. Fourier transform is intuitively illustrated in BetterExplained [8, 3Blue1Brown’s [9], and Math StackExchange [16]. Below is notes taken based on [9].
A concrete example to apply Fourier transform is to analyze a signal which mixes two different signals, each of a constant frequency. In the example, suppose we can only measure the blended signal (green), while we want to tell posthumously that it actually composes of the pink signal (for example, 2Hz) and the yellow signal (for example, 3Hz).
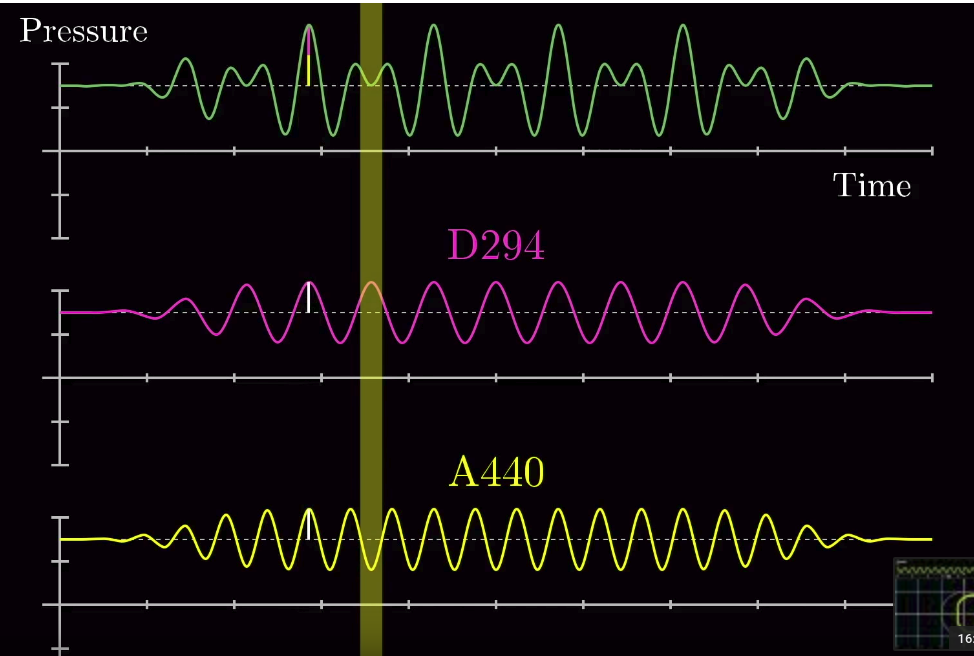
The magic idea of Fourier transform is that if you transform the signal measured in the Pressure vs. Time space into a rotating motion in a 2D plane, it will looks like the diagram below:
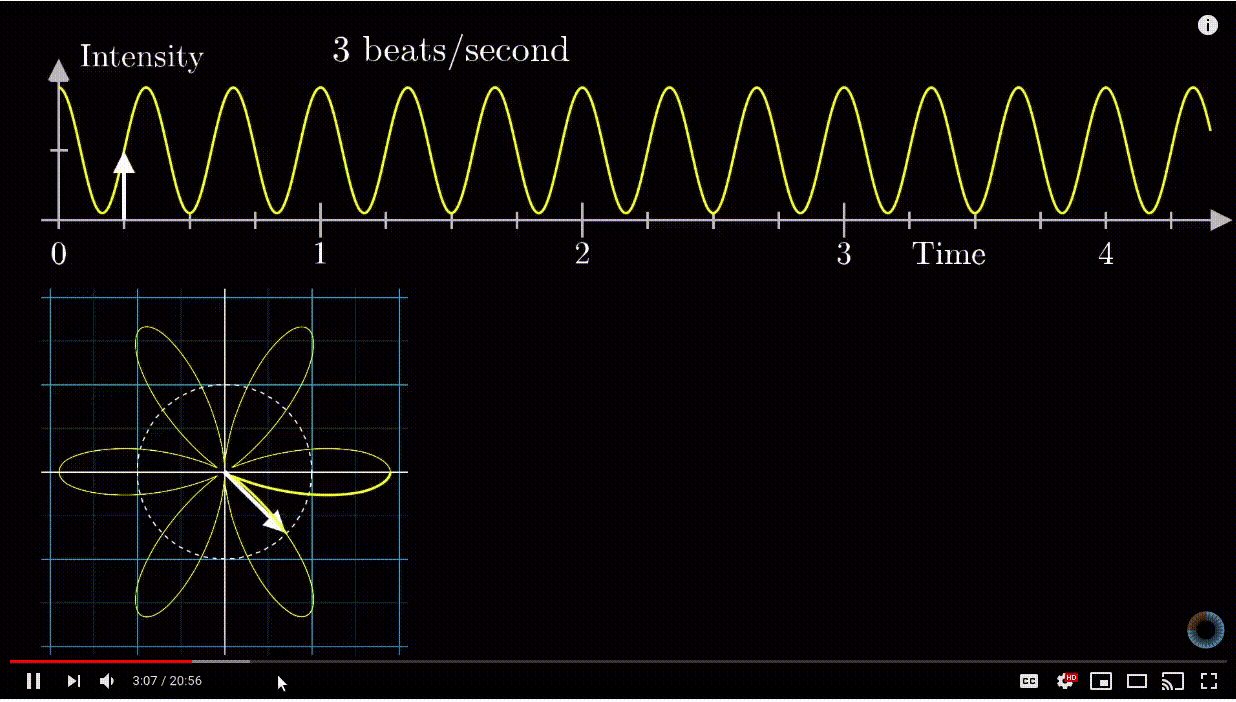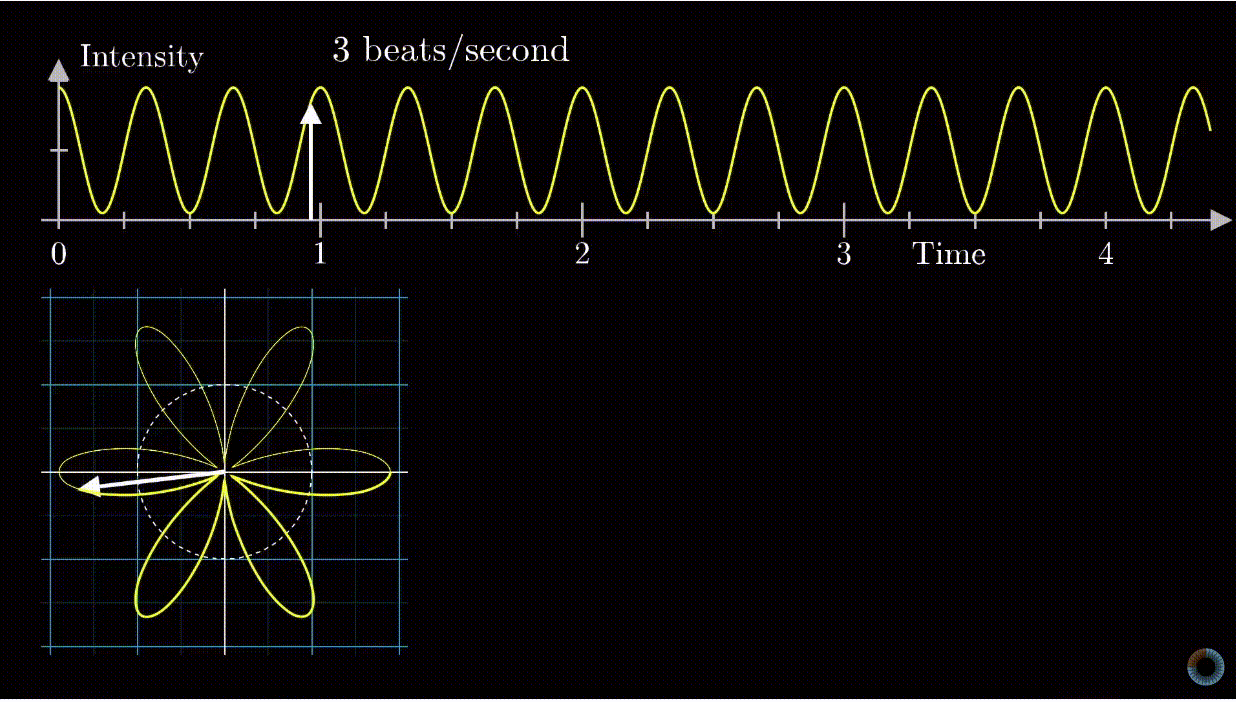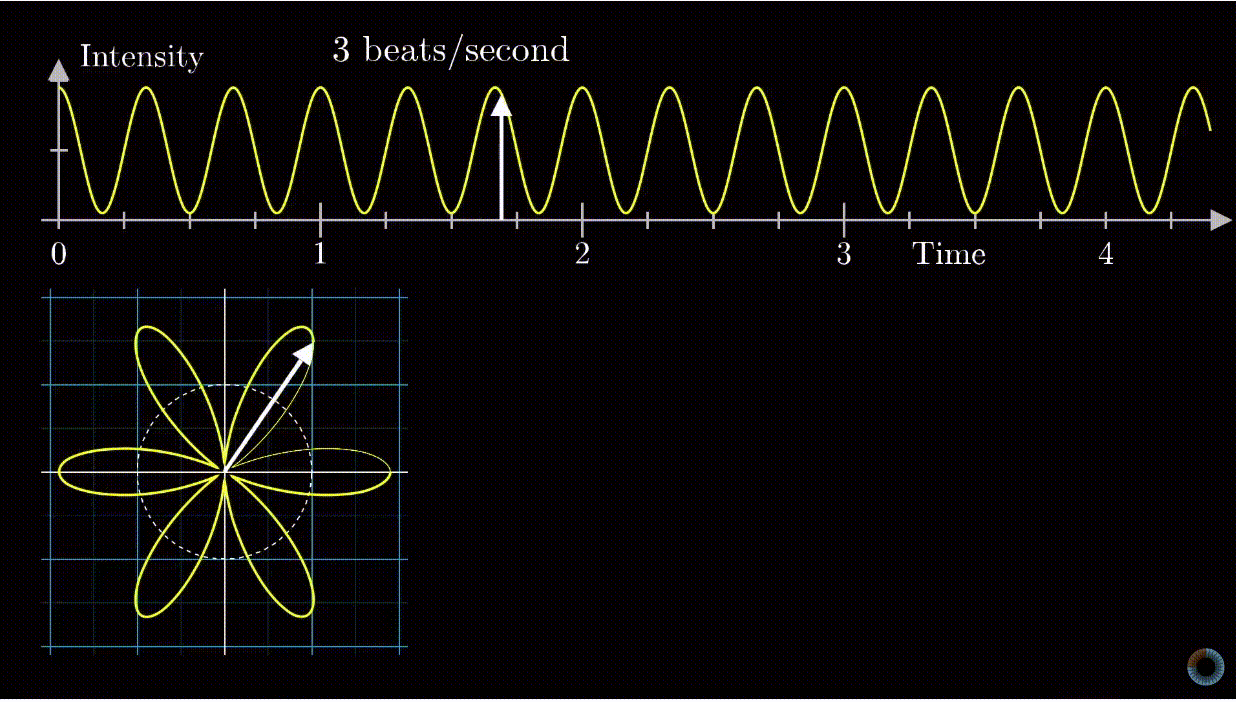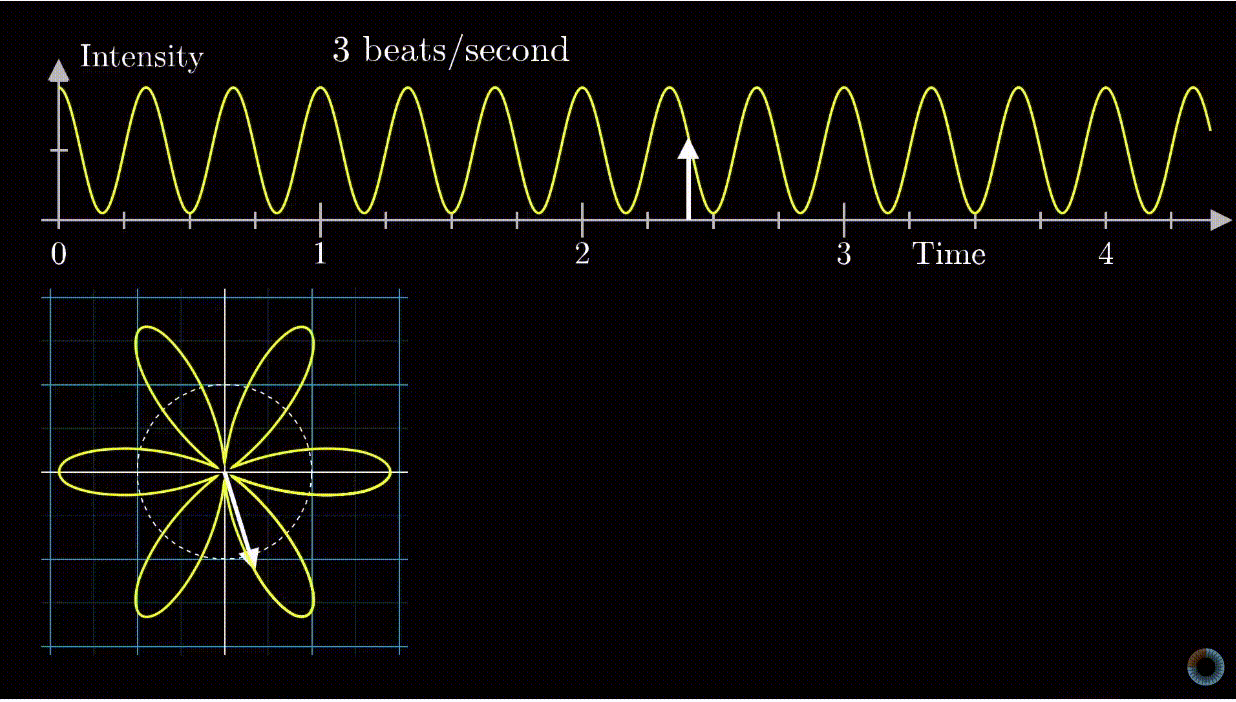
Depending on the frequency of rotating motion, the diagram on the 2D plane may be different.
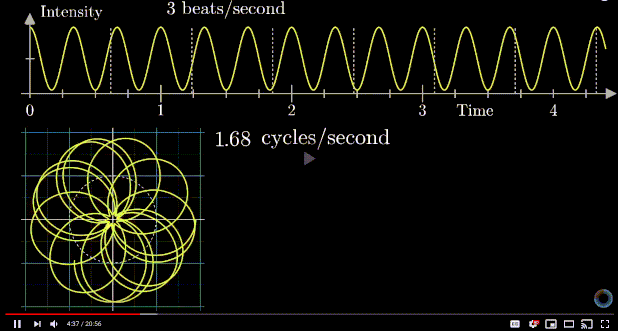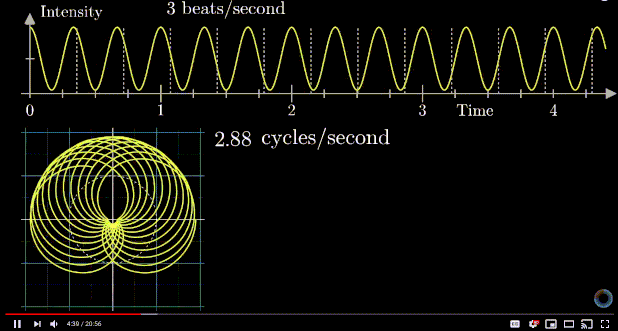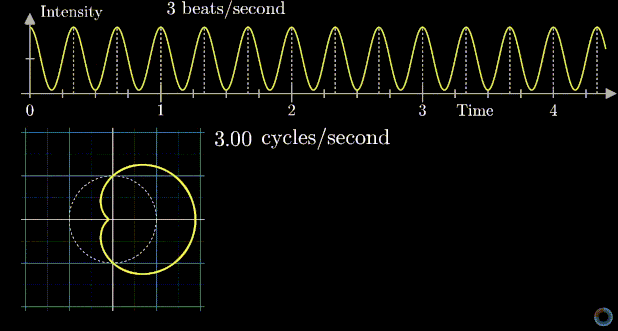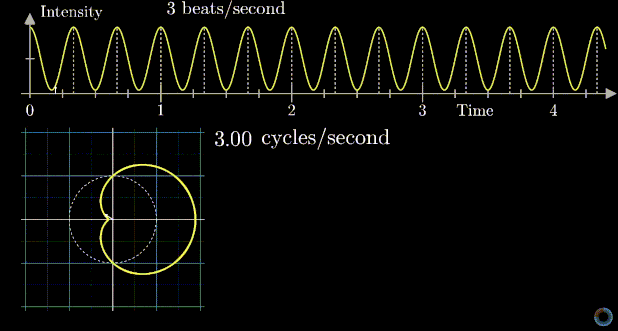
An important observation is that if you look at the center of mass of the diagram based on any rotating frequency, you will see that the center of mass is farthest away from the origin when the frequency of rotating motion matches the frequency of either individual signal (2Hz or 3Hz).
Therefore, to recover original signals, we need to try out every possible frequency of rotating motion and just obtain the location of the center of mass of the diagram for each frequency of rotating motion, then we would know what are the frequencies of the original individual signals.
The center of mass can be obtained by sampling and averaging of the data points on the diagram, while the diagram is mapped onto a 2D complex plane:
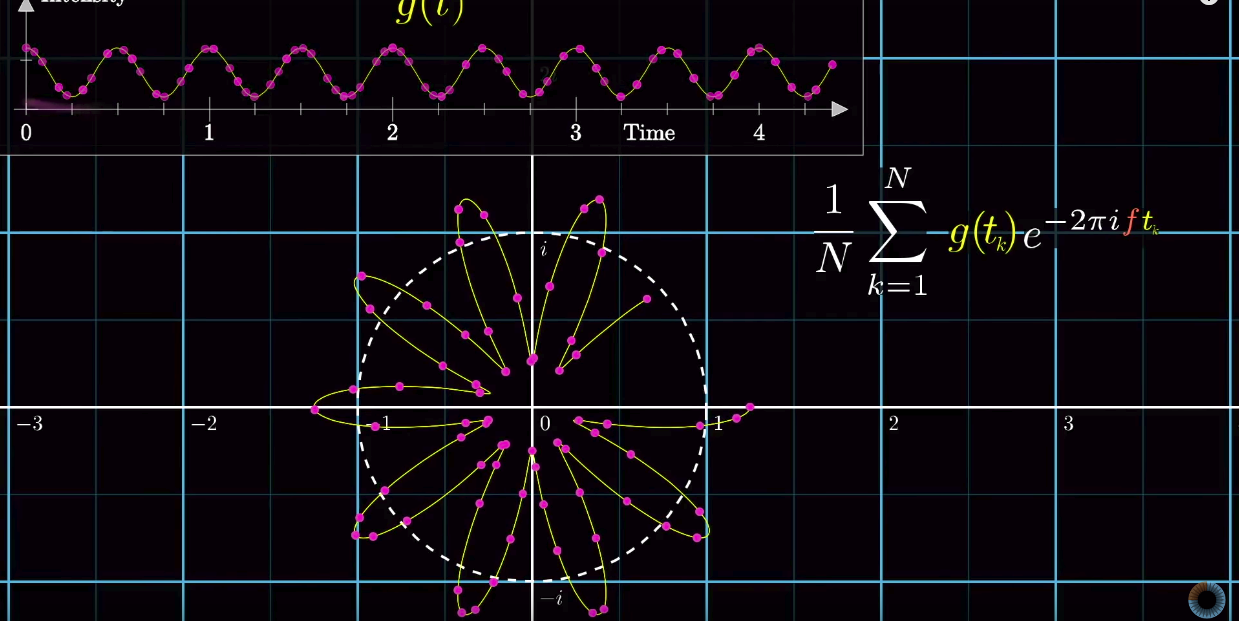
When the number of samples goes to infinite, it becomes integral.
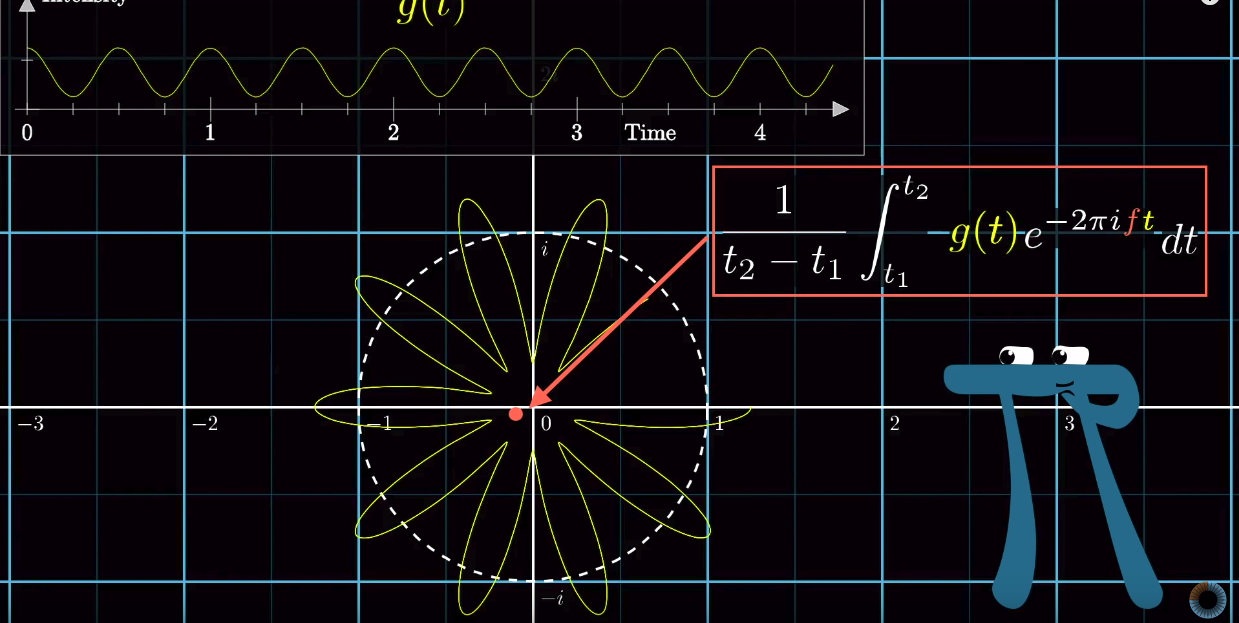
Fourier transform, following this idea, is only different in that the integral is from negative infinity to positive infinity, and there is no final average over time (![]() removed).
removed).
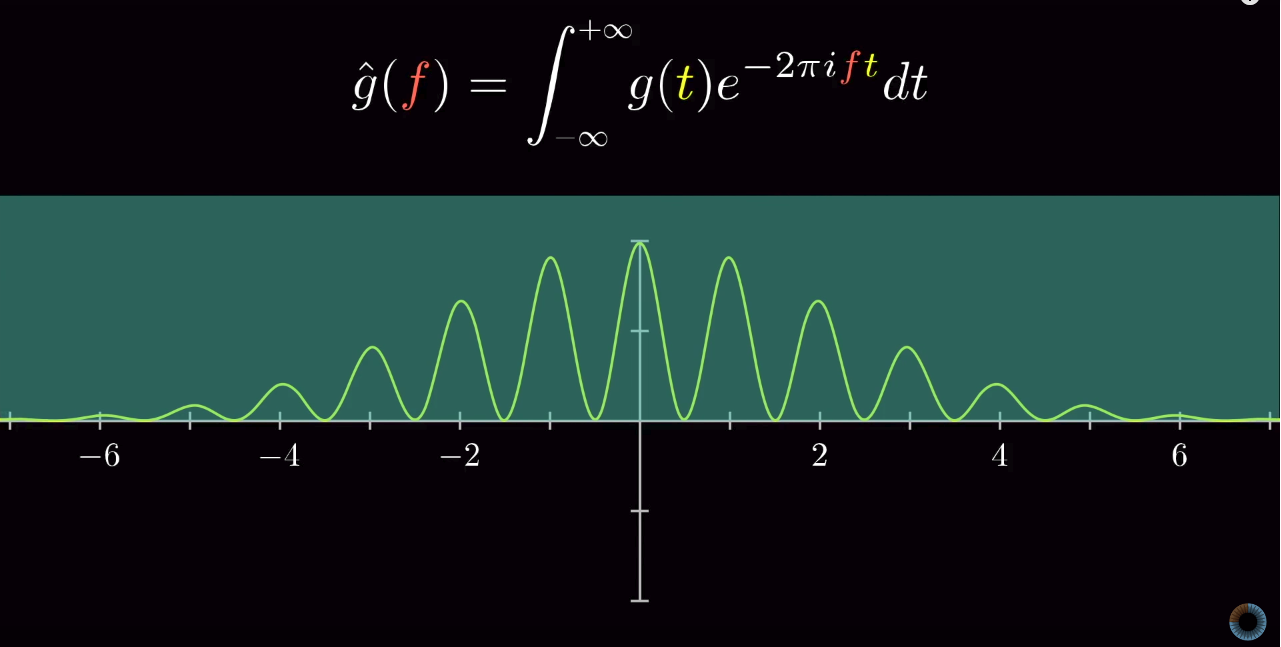
Here is an example [15] where Fourier transform is applied on ![]() . The result is two Dirac Delta functions on the frequency domain.
. The result is two Dirac Delta functions on the frequency domain.
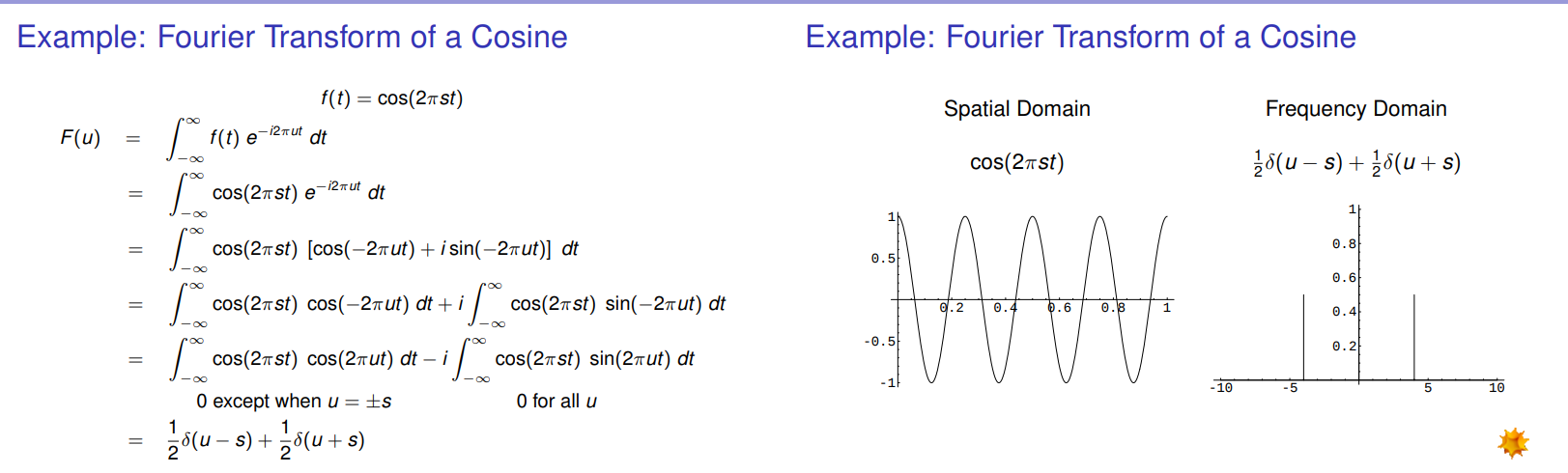
The transform process is based on trigonometry. In the second to the last equation, when ![]() ,
, 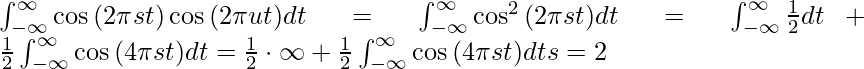
According to [10], although ![]() does not converge, I have seen many places [15, 18] treating
does not converge, I have seen many places [15, 18] treating ![]() . I don’t understand this, but I could think it in an intuitive way: although
. I don’t understand this, but I could think it in an intuitive way: although ![]() does not converge, its values is confined in a limited range (
does not converge, its values is confined in a limited range (![]() ). Compared to the infinity we obtain from
). Compared to the infinity we obtain from ![]() , the value of
, the value of ![]() is infinitely close to zero.
is infinitely close to zero.
Another idea is to solve the integration based on Euler’s formula [17][20]. Based on Euler’s formula, we can get ![]() . Also, Dirac Delta function is defined as (its proof, which I don’t fully understand, can be found on [11, 12, 13]):
. Also, Dirac Delta function is defined as (its proof, which I don’t fully understand, can be found on [11, 12, 13]):
![]()
Or equivalently, ![]()
Therefore, we can finally get (based on [17][20], with a little difference because they transform ![]() rather than
rather than ![]() ):
):
 :
:
According to the linear property of Fourier transform [19], if a blended signal is the sum of several signals (for example, ![]() , then the resultant Fourier transform is the sum of several Dirac functions. That’s how Fourier transform extracts individual signals from the mixed one! And the connection between Euler’s formula and Fourier transform is that the integration required by Fourier transform to obtain the center of mass of the rotation diagram, if connected to Euler’s formula, can be calculated very easily.
, then the resultant Fourier transform is the sum of several Dirac functions. That’s how Fourier transform extracts individual signals from the mixed one! And the connection between Euler’s formula and Fourier transform is that the integration required by Fourier transform to obtain the center of mass of the rotation diagram, if connected to Euler’s formula, can be calculated very easily.
[14] is another illustrative video showing that any signal we can measure can be actually seen as a combination of an infinite number of sine waves. For repeating waves in time space, its Fourier transform may shown as discrete frequency spectrum (like several Dirac deltas). However, non-repeating waves in time space may result to continuous frequency spectrum after Fourier transform. This is interesting to know but I will not explore further within this article.

References
[1] https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/
[4] https://www.youtube.com/watch?v=qpOj98VNJi4
[5] https://en.wikipedia.org/wiki/Euler%27s_formula#Using_power_series
[6] https://www.youtube.com/watch?v=F_0yfvm0UoU
[7] https://www.youtube.com/watch?v=mvmuCPvRoWQ
[8] https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
[9] https://www.youtube.com/watch?v=spUNpyF58BY
[10] https://www.wolframalpha.com/input/?i=integrate+cos(x)+from+-infinity+to+infinity
[11] http://fourier.eng.hmc.edu/e102/lectures/ExponentialDelta.pdf
[13] https://www.quora.com/Why-are-integrals-of-complex-exponentials-delta-functions
[14] https://www.youtube.com/watch?v=r18Gi8lSkfM
[15] https://www.astro.umd.edu/~lgm/ASTR410/ft_ref2.pdf
[16] https://math.stackexchange.com/questions/1002/fourier-transform-for-dummies
[17] https://www.youtube.com/watch?v=jPM76k-uNnA
[18] https://blog.mide.com/fourier-transform-basics
[19] https://en.wikipedia.org/wiki/Fourier_transform#Properties_of_the_Fourier_transform