I am introducing some basic definitions of abstract algebra, structures like monoid, groups, rings, fields and vector spaces and homomorphism/isomorphism.
I find the clear definitions of structures from [1]:

Also, the tables below show a clear comparisons between several structures [2,3]:
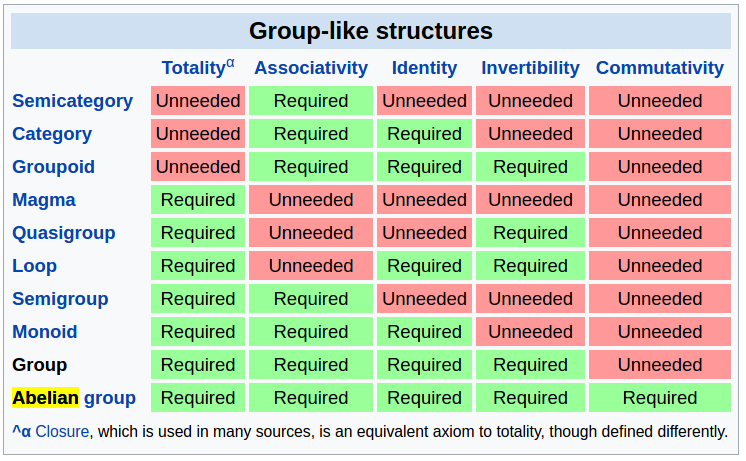
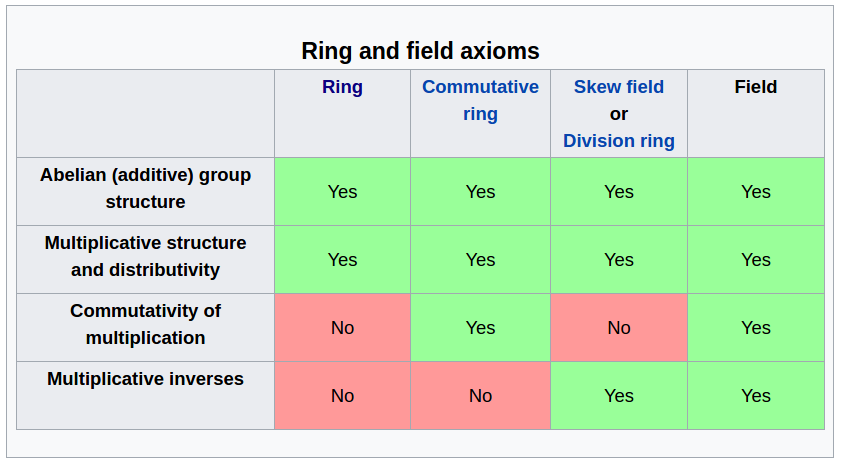
All these structures are defined with both a set and operation(s). Based on [4], a monoid is an abstraction of addition. A group is an abstraction of addition and subtraction. A ring adds multiplication but not necessarily division. A field adds division. Therefore, ultimately, a field is the “biggest” set (compared to monoid, group and ring), on which are defined addition, subtraction, multiplication and division. Similar idea is also illustrated in [6].
As also pointed out by [6], since we are dealing with abstract algebra, calling operations with the names “addition, subtraction, multiplication, division” is just a convention. The operations are applied on sets that might be very different with real numbers or integers. They are analogous but not necessarily the same as what we understand for the addition, subtraction, multiplication and division on real numbers.
We can safely say that every ring is a group, and every field is a ring [5]:

A vector space over a field $latex F$ is a set $latex V$ with two operations, vector addition and scalar multiplication, satisfying the ten axioms listed below [10, 11, 22]:

To me, Euclidean vector space is the most familiar vector space as an example.
Now, there are several subcategories of vector spaces. One kind is normed vector space [12], meaning that the norm of vectors is defined in the vector space. Another kind of vector space is called inner product vector space [13], which is a vector space with a mapping function called “inner product” that maps any pair of vectors (over field F) to a scalar in F. (Note that I used to think “inner product” and “dot product” are exchangeable in their meanings. Now I know that “inner product” is just a name of an operator that maps two vectors into a field. “dot product” is the name of “inner product” in Euclidean space.) More specially, an operator can be called “inner product” if it satisfies [26]:

The inner product between a vector and itself naturally induces the norm of it. Hence, an inner product vector space must be a normed vector space. BTW, along the search of inner product vector space, I found a good textbook [14]. Another kind vector space is called metric vector space, which means the distance between any two vectors $latex d(x,y), x,y \in V$ is defined. A normed vector space must be a metric vector space because the definition of metric can be induced from the definition of norm. (book page 59 in [25]). Bear in mind that a metric space may not be a normed space, and a normed space may not be an inner product space. You can have a basic intuition of how spaces from metric space, to normed space, to inner product space, become more and more powerful [27].
A Cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses [15]. The definition [Appendix in 16] is that in a vector space $latex V$, you have a Cauchy sequence of vectors $latex v_1, v_2, \cdots$ Then, for any $latex \epsilon > 0$ there is a corresponding $latex k$ such that $latex \lVert v_i – v_j \rVert < \epsilon$ for all $latex i,j \geq k$. A normed vector space $latex V$ is complete if every Cauchy sequence in $latex V$ is convergent in $latex V$, i.e., the limit point of every Cauchy sequence is also in $latex V$. A complete normed vector space is called Banach space [24]. A complete inner product vector space is Hilbert space [17]. An incomplete inner product vector space is called pre-Hilbert space. Every Euclidean space is finite and a Hilbert space (because dot product is defined in Euclidean space and Euclidean space is complete). However, a Hilbert space is not necessarily a Euclidean space since its dimension can be infinite. A famous example of Hilbert space with infinite dimensions is $latex \mathcal{l}^2$:


Although we just talked about sequence space $latex \ell^2$ has infinite dimensions, we have not defined what is dimension of a vector space [25]:


Now let’s look at homomorphism:

Note that the map is between two structures of the same type. That means, the map preserves some properties of the two structures, hence the name: homo (same) + morphism (shape,form).
By convention, linear transformation of vector spaces is called vector space homomorphism [18]:

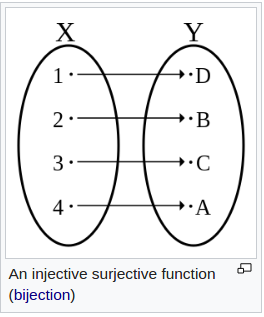
For most algebra structures, isomorphism is a homomorphism equipped with a mapping that is bijective (has inverse and one-to-one correspondence) [7]. That means. after a mapping or the reverse of it, isomorphism preserves the relationships between elements of the two sets. For example [8]:
Knowing two structures are isomorphic has several advantages, with the most prominent one being to establish the knowledge of a more complicated set by studying a simpler set which is isomorphic [8, 9].
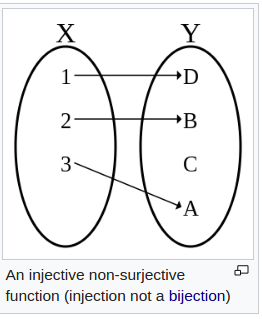
There are several types of mappings in abstract algebra.
injective:
surjective:
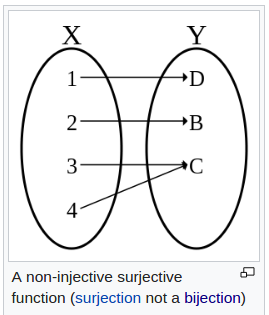
and bijective:
A linear operator is [25]:

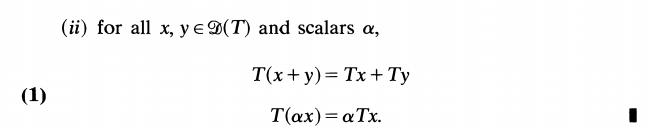
A linear functional $latex f$ is a linear operator with its domain as a vector space over a field $latex F$ and its range as scalars of $latex F$ [20]:

The set of all linear functionals that map from $latex V$ to $latex F$ form a vector space $latex V^*$ called dual space, with also two operations, addition and scalar multiplication [19]:

There is also a double dual space, $latex V^{**}$, which is the dual space of $latex V^*$. It is very obscure to understand this concept. My understanding is that $latex V^*$ contains a set of linear functionals, and $latex V^{**}$ contains a set of linear functionals of linear functionals. If we suppose there is a linear functional $latex f \in V^*$ and a linear functional $latex \Phi \in V^{**}$, then we want that $latex \Phi(f)$ should return a scalar. In a generative way, you can think that every $latex \Phi \in V^**$ is created by first selecting a $latex v \in V$, and let $latex \Phi(f)=f(v)$. In “$latex f(v)$”, treat $latex f$ as a variable and $latex \cdot(v)$ as the linear functional $latex \Phi$. More details can be found in [23].
I was surprised to learn that linear operators (and linear functionals) actually have norms. The definition of norms of linear operators is [25]:


Non degenerate bilinear mapping is [21]:
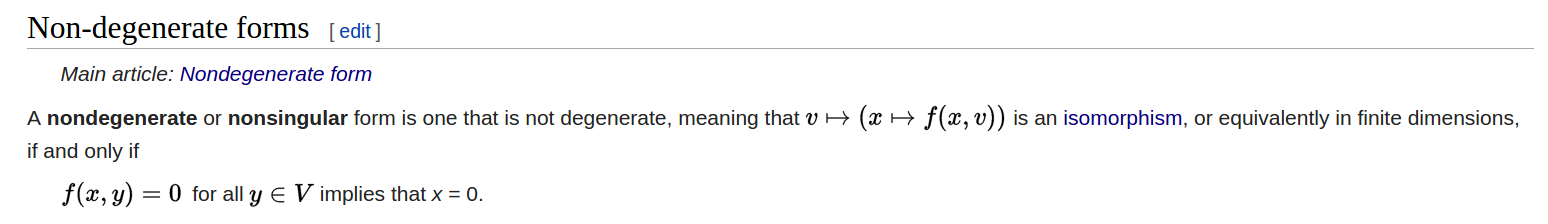
Reference
[1] groups_rings_fields_vector_spaces from: http://people.csail.mit.edu/madhu/ST12/scribe/lect03.pdf
[2] https://en.wikipedia.org/wiki/Group_(mathematics)#Generalizations
[3] https://en.wikipedia.org/wiki/Field_(mathematics)#Related_algebraic_structures
[4] http://math.stackexchange.com/a/730768/235140
[5] http://math.stackexchange.com/a/80/235140
[6] http://math.stackexchange.com/a/1425663/235140
[7] http://aleph0.clarku.edu/~ma130/isomorphism.pdf
[8] https://www.britannica.com/topic/isomorphism-mathematics
[9] http://math.stackexchange.com/questions/441758/what-does-isomorphic-mean-in-linear-algebra
[10] http://mathworld.wolfram.com/VectorSpace.html
[11] https://en.wikipedia.org/wiki/Algebra_over_a_field
[12] https://en.wikipedia.org/wiki/Normed_vector_space
[13] https://en.wikipedia.org/wiki/Inner_product_space
[14] http://www.linear.axler.net/InnerProduct.pdf
[15] https://en.wikipedia.org/wiki/Cauchy_sequence
[16] http://www.cs.columbia.edu/~risi/notes/tutorial6772.pdf
[17] https://en.wikipedia.org/wiki/Hilbert_space
[18] http://math.stackexchange.com/a/29962/235140
[19] https://en.wikipedia.org/wiki/Dual_space
[20] https://en.wikipedia.org/wiki/Linear_form
[21] https://en.wikipedia.org/wiki/Degenerate_bilinear_form
[22] http://math.stackexchange.com/questions/49733/prove-in-full-detail-that-the-set-is-a-vector-space
[23] http://math.stackexchange.com/questions/170481/motivating-to-understand-double-dual-space
[24] https://en.wikipedia.org/wiki/Banach_space
[26] http://people.math.gatech.edu/~heil/handouts/appendixa.pdf