This post explains my understanding in a proposed greedy algorithm for the maximum weighted matching problem.
The greedy algorithm goes as follows (listed by this paper in Introduction section):
It is claimed that the greedy algorithm is a 2 approximation, i.e., greedy result >= 1/2 optimal result.
The document where the greedy algorithm is proposed is erroneous therefore the proof for the 2 approximation is unreadable. Fortunately, another guy put his words to explain it: http://math.stackexchange.com/questions/1146224/proof-for-why-maximum-weight-matching-using-greedy-guarantees-at-least-1-2-the-w. However, I think further explanation is still needed to facilitate the understanding. Here is my thoughts:
If any edge $latex e$ belongs to the optimal matching $latex M^*$ but not the greedy matching $latex M$, it must be due to that at least one of its two vertices is incident on another edge $latex e’$ which is included in the greedy matching $latex M$. Due to the greedy algorithm, $latex w(e’) > w(e)$ otherwise the greedy algorithm could have selected $latex e$. Moreover, $latex e’ \in M \setminus M^*$ because, if $latex e’ \in M^*$, and we know $latex e \in M^*$, then $latex M^*$ contains two edges incident on the same node by contradiction.
Each $latex e \in M^* \setminus M$ can be linked to an edge $latex e’ \in M \setminus M^*$ where $latex w(e’)>w(e)$. The same edge $latex e’$ can be counted at most twice if traversing all $latex e$ (maybe one endpoint of $latex e’$ touches an edge $latex e_1 \in M^* \setminus M$ and maybe the other endpoint of $latex e’$ touches another edge $latex e_2 \in M^* \setminus M$. ) Therefore, $latex \sum\limits_{e \in M^* \setminus M} w(e) < 2 * \sum\limits_{e’ \in M \setminus M^*} w(e’)$. 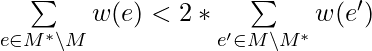We can also obtain trivially, under the assumption that all weights are positive, that $latex \sum\limits_{e \in M \cap M^*} w(e) < 2 * \sum\limits_{e \in M \cap M^*} w(e)$. Adding the two inequalities together, we get $latex \sum\limits_{e \in M^*} w(e) < 2 * \sum\limits_{e’ \in M} w(e’)$.
The greedy algorithm is not applicable to maximum weighted perfect matching because it is not guaranteed to find perfect matching. (perfect matching: every vertex is incident on exactly one edge in the matching. ) Provided that we have the following inequalities:
optimal result for maximum weighted matching > optimal result for maximum weighted perfect matching
1/2 * optimal result for maximum weighted matching <= greedy result for maximum weighted matching
, we conclude that the greedy result for maximum weighted matching can loosely be used for maximum weighted perfect matching, if perfect matching is not strictly required. It is more appealing when the graph is a complete graph. In a complete graph, the greedy method returns a perfect matching.
The greedy algorithm takes $latex O(m\log m)$ to sort edge weights ($latex m=|E|$). In a complete graph where $latex m=n^2$ ($latex n=|V|$), the greedy algorithm takes $latex O(n^2 \log n)$, a little better than existing $latex O(n^3)$ methods (such as this) to solve maximum weighted perfect matching. There is also an $latex 1-\epsilon$ approximation method running in $latex O(m \epsilon^{-1} \log \epsilon^{-1})$. However, the method is much more complicated.