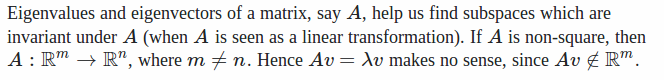This topic has been in my wish list for a long time. I will try to articulate my understanding of eigenvector and eigenvalue after digestion informative materials from different sources.
First of all, we can consider multiplication between a square matrix ![]() and a vector
and a vector ![]() as a transformation of
as a transformation of ![]() such that
such that ![]() is rotated and scaled. By definition, eigenvectors of
is rotated and scaled. By definition, eigenvectors of ![]() are vectors on the directions on which
are vectors on the directions on which ![]() has invariant rotation transformation, i.e.,
has invariant rotation transformation, i.e., ![]() .
.
What kind of matrices have eigenvectors? Only square matrices are possible to have eigenvectors. This is because:
ref: http://math.stackexchange.com/a/583976/235140
However, not all square matrices have eigenvectors: http://math.stackexchange.com/a/654713/235140
Two useful interpretations of eigenvectors if you regard a square matrix as rotation + scale transformation:
- no other vectors when acted by this matrix can be stretched as much as eigenvectors. (ref: http://math.stackexchange.com/a/243553/235140)
- eigenvectors keep the same direction after the transformation. (ref: https://www.quora.com/What-do-eigenvalues-and-eigenvectors-represent-intuitively)
Now, let’s see the scenarios in computer science realm where eigenvectors/eigenvalues play a role.
1. PCA
Now we look at all kinds of matrics including square matrices. One way to understand a matrix is that it represents a coordination system. Suppose ![]() is a matrix and
is a matrix and ![]() is a column vector, then one way to interpret
is a column vector, then one way to interpret ![]() is that every row of the matrix
is that every row of the matrix ![]() is a base vector of its coordination system. Every component of
is a base vector of its coordination system. Every component of ![]() is a dot product of a row of
is a dot product of a row of ![]() and
and ![]() , which can be seen as a kind of projection from
, which can be seen as a kind of projection from ![]() on the corresponding row of
on the corresponding row of ![]() .
.
If now we have a transformation matrix ![]() in which rows are base vectors of some coordination system,
in which rows are base vectors of some coordination system, ![]() is data matrix where
is data matrix where ![]() is the number of data points and
is the number of data points and ![]() is the number of dimensions, then
is the number of dimensions, then ![]() is a dimension reduced matrix of
is a dimension reduced matrix of ![]() such that every column of
such that every column of ![]() is representation of every column of
is representation of every column of ![]() using base vectors in
using base vectors in ![]() .
.
PCA is trying to find such ![]() that not only reduces the dimension of
that not only reduces the dimension of ![]() but also satisfies other properties. And what it concludes is that
but also satisfies other properties. And what it concludes is that ![]() is a matrix in which rows are eigenvectors of
is a matrix in which rows are eigenvectors of ![]() ‘s covariance matrix. (ref: https://czxttkl.com/?p=339, https://www.cs.princeton.edu/picasso/mats/PCA-Tutorial-Intuition_jp.pdf)
‘s covariance matrix. (ref: https://czxttkl.com/?p=339, https://www.cs.princeton.edu/picasso/mats/PCA-Tutorial-Intuition_jp.pdf)
2. PageRank / Stationary distribution of Markov chains
Both try to find eigenvectors with eigenvalues equal to 1: ![]() . In PageRank,
. In PageRank, ![]() is a fractional PageRank constribution link matrix in which
is a fractional PageRank constribution link matrix in which ![]() is the page rank contributed to webpage
is the page rank contributed to webpage ![]() when webpage
when webpage ![]() links it.
links it. ![]() is the PageRank value vector for all web pages that we want to calculate. When calculating stationary distribution of Markov States,
is the PageRank value vector for all web pages that we want to calculate. When calculating stationary distribution of Markov States, ![]() is simply a transition matrix denoting pairwise transition probabilities between nodes while
is simply a transition matrix denoting pairwise transition probabilities between nodes while ![]() is the ultimate stationary distribution of nodes.
is the ultimate stationary distribution of nodes.