Leetcode 115: Distinct Subsequences

https://leetcode.com/problems/distinct-subsequences/

Given a string S and a string T, count the number of distinct subsequences of T in S.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

Here is an example:
S = "rabbbit", T = "rabbit"

Return 3.

 

The question is a bit ambiguous. Please see the following link for clarification.

https://leetcode.com/discuss/599/task-clarification

 

Code

class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        if s is None or t is None:
            return 0
        if len(t) > len(s):
            return 0
            
        num = [[1] + [0] * (len(t)) for i in range(len(s)+2)]   # a (len(s)+1)*(len(t)+1) matrix

        for i in xrange(1, len(s)+1):
            for j in xrange(1, min(i, len(t))+1):
                num[i][j] = num[i-1][j] 
                if s[i-1] == t[j-1]: num[i][j] += num[i-1][j-1]

        return num[len(s)][len(t)] 
        

 

Idea

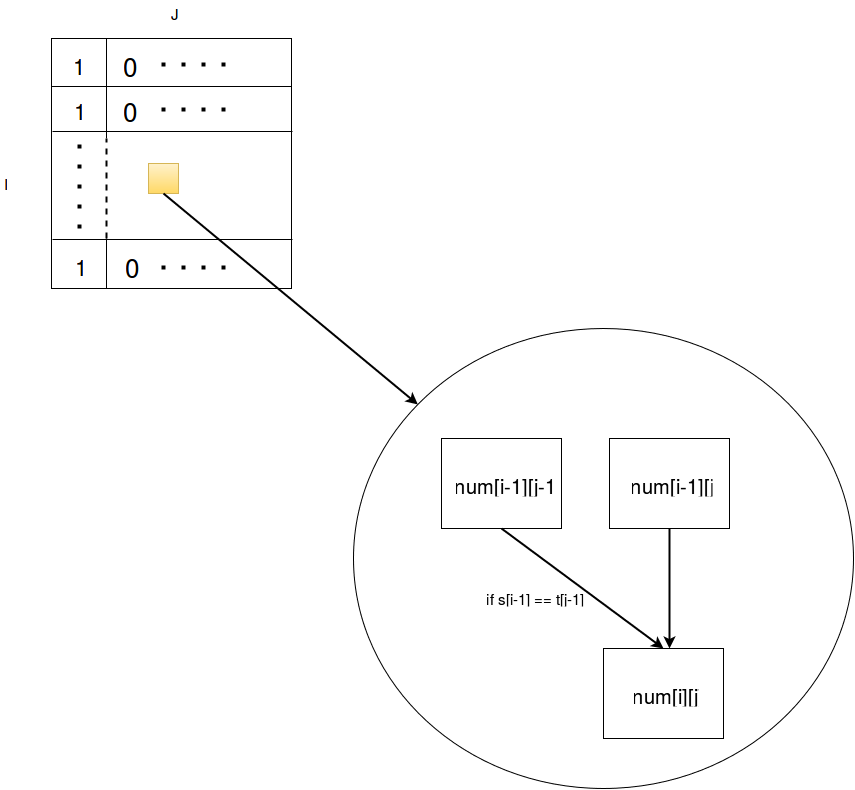
Use dynamic programing to tackle this problem. Create an array, `num`, in which `num[i][j]` denotes the number of distinct subsequences same to `t[:j]` in `s[:i]`.  For `num[i][j] = 0` where `i <j` because you can’t find subsequences longer than the full sequence. `num[i][0]` is always 1 because every full sequence has a subsequence of empty string. 

Therefore, the array `num` is initialized as:

Since we are using dynamic programming, we need to find the formula to update `num[i][j]`. We propose that `num[i][j]=num[i-1][j] + (s[i-1]==t[j-1]?num[i-1][j-1]:0)`. In other words, the  distinct subsequences equal to `t[:j]` in `s[:i]` come from two parts:

1. the distinct subsequences equal to `t[:j]` in `s[:i-1]`. This is equivalent to discard `s[i-1]` and check the number of distinct subsequences in `s[:i-1]`.
2. if `s[i-1]==t[j-1]`, the distinct subsequences equal to `t[:j-1]` in `s[i-1]`. This is equivalent to discard `s[i-1]` and `t[j-1]` and compare the two remaining strings.

The update rule can be visualized as:

Overall, this algorithm takes O(N^2) time to update the full `num` array and takes O(N^2) space to store `num` array. (Suppose O(N) is the length of `s` and `t`).

 

More

2D space in dynamic programming can often be reduced to 1D space. Our code updates` num` in a “column-first-row-after” manner. Essentially, we only need to have the previous row vector to update the current row vector. Note that `num[i][j]` needs the values from `num[i-1][j-1]` and `num[i-1][j]`. In order to not erase necessary values in `num[i-1][j]` and `num[i-1][j-1]`, we need to update the row vector backwards.

class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        if s is None or t is None:
            return 0
        if len(t) > len(s):
            return 0
            
        num = [1] + [0] * (len(t)) 

        for i in xrange(1, len(s)+1):
            for j in xrange(min(i, len(t)), 0, -1):
                if s[i-1] == t[j-1]: num[j] += num[j-1]

        return num[len(t)] 
        

Now, the algorithm takes O(N^2) time and only O(N) space.