https://leetcode.com/problems/linked-list-cycle-ii/
Linked List Cycle II
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Note: Do not modify the linked list.
Follow up:
Can you solve it without using extra space?
Idea
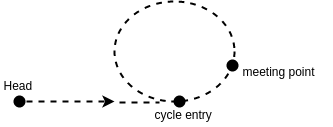
As the plot shows, we have a linked list with a cycle. Suppose it has 1-based index. Head has index `h`. The entry of the cycle has index `e`. We reuse the code from the previous code in which we have a slow pointer and a fast pointer (traversing the list twice as fast as the slow pointer.) The point where the fast and the slow pointer meet has index `m`. We also set the length of the cycle as C.
When the fast and the slow pointers meet:
- the number of the nodes the slow pointer has passed: e + (m-e) + n1*C
- the number of the nodes the fast pointer has passed: e + (m-e) + n2*C
- We also know that 2(e+(m-e)+n1*C) = e+(m-e)+n2*C, because the fast pointer travels twice as fast as the slow pointer.
By canceling same terms on both sides of the equation, we finally get:
e = C-(m-e) + n3*C
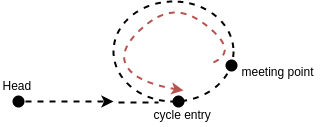
where n3 is a non-negative integer unknown and unimportant to us. C-(m-e) is the distance between the meeting point and the cycle entry along the direction of the linked list. (See the red path in the plot below).
Now it becomes easy to find the value of `e`. You now create a new pointer, `p`, starting from head. Let the slow pointer and `p` travel one node by one node until the two meets. The point where they meet should be the entry of the cycle.
Code
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def detectCycle(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if not head:
return None
slow = fast = head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
if slow == fast: # Find cycle
p = head
while p != slow:
p = p.next
slow = slow.next
return slow
return None
Reference
https://leetcode.com/discuss/16567/concise-solution-using-with-detailed-alogrithm-description