Leetcode 156: Binary Tree Upside Down

https://leetcode.com/problems/binary-tree-upside-down/

Binary Tree Upside Down

Total Accepted: 4861 Total Submissions: 13934 Difficulty: Medium

Given a binary tree where all the right nodes are either leaf nodes with a sibling (a left node that shares the same parent node) or empty, flip it upside down and turn it into a tree where the original right nodes turned into left leaf nodes. Return the new root.

For example:
Given a binary tree {1,2,3,4,5},

return the root of the binary tree [4,5,2,#,#,3,1].

confused what "{1,#,2,3}" means? > read more on how binary tree is serialized on OJ.

OJ’s Binary Tree Serialization:

The serialization of a binary tree follows a level order traversal, where ‘#’ signifies a path terminator where no node exists below.

Here’s an example:

The above binary tree is serialized as "{1,2,3,#,#,4,#,#,5}".

Code

class Solution:
        # @param root, a tree node
        # @return root of the upside down tree
        def upsideDownBinaryTree(self, root):
            # take care of the empty case
            if not root:
                return root
            # take care of the root
            l = root.left
            r = root.right
            root.left = None
            root.right = None
            # update the left and the right children, form the new tree, update root
            while l:
                newL = l.left
                newR = l.right
                l.left = r
                l.right = root
                root = l
                l = newL
                r = newR
            return root

Idea

First, let’s walk through what is called “upside down”. I draw an example plot. The original tree roots at 7. To turn it upside down, you first mirror it along a horizontal line. Then, for any branch stretching towards right top (marked as red), you make it as left leaf.

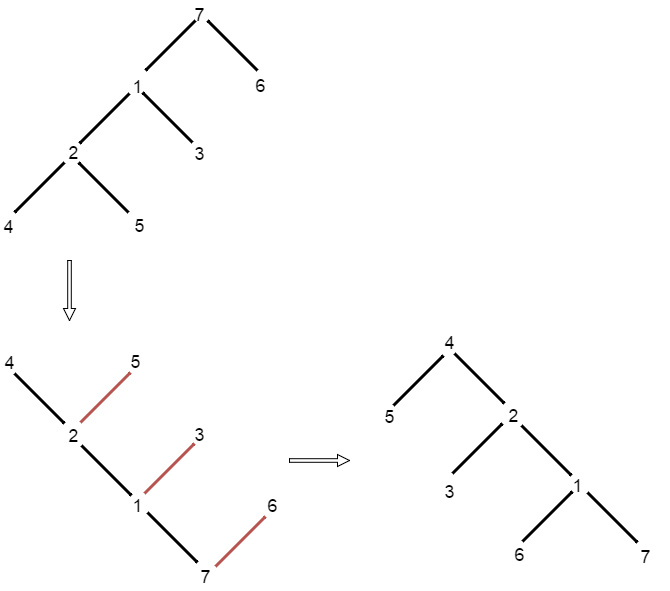
Now, the basic idea is to go though from the original root (7), make root’s left child (1) as new parent whose left child will be the original root’s right left (6) and right child will be the original root (7). After that, you set new root to root.left (1), and process it in the same way. As pointed out by (https://leetcode.com/discuss/18410/easy-o-n-iteration-solution-java), the core idea is to “Just think about how you can save the tree information you need before changing the tree structure“.

Reference

https://leetcode.com/discuss/30902/iteration-python-solution

https://leetcode.com/discuss/18410/easy-o-n-iteration-solution-java

Leetcode 156: Binary Tree Upside Down

Binary Tree Upside Down

Leave a comment

Cancel reply