https://leetcode.com/problems/the-skyline-problem/
The Skyline Problem
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
- The number of buildings in any input list is guaranteed to be in the range
[0, 10000]. - The input list is already sorted in ascending order by the left x position
Li. - The output list must be sorted by the x position.
- There must be no consecutive horizontal lines of equal height in the output skyline. For instance,
[...[2 3], [4 5], [7 5], [11 5], [12 7]...]is not acceptable; the three lines of height 5 should be merged into one in the final output as such:[...[2 3], [4 5], [12 7], ...]
Credits:
Special thanks to @stellari for adding this problem, creating these two awesome images and all test cases.
I failed to do it myself. My first thought was to traverse each building once and determine all skyline points that should be added. However, `O(N)` seems unable to solve this problem. Because there are many cases that you need to go back to check already added skyline points.
The correct idea is to use merge and sort, though there are so many edge cases. Two solutions that seem easy to understand:
https://leetcode.com/discuss/37444/my-220ms-divide-and-conquer-solution-in-python-o-nlogn
http://www.programcreek.com/2014/06/leetcode-the-skyline-problem-java/
http://www.geeksforgeeks.org/divide-and-conquer-set-7-the-skyline-problem/
One piece of code from them:
#
class Solution:
# @param {integer[][]} buildings
# @return {integer[][]}
def getSkyline(self, buildings):
if buildings==[]:
return []
if len(buildings)==1:
return [[buildings[0][0],buildings[0][2]],[buildings[0][1],0]]
mid=(len(buildings)-1)/2
left=self.getSkyline(buildings[0:mid])
right=self.getSkyline(buildings[mid:])
return self.merge(left,right)
def merge(self,left,right):
i=0
j=0
result=[]
h1=None
h2=None
while i<len(left) and j<len(right):
if left[i][0]<right[j][0]: # Condition 1
h1=left[i][1]
new=[left[i][0],max(h1,h2)]
if result==[] or result[-1][1]!=new[1]:
result.append(new)
i+=1
elif left[i][0]>right[j][0]: # Condition 2
h2=right[j][1]
new=[right[j][0],max(h1,h2)]
if result==[] or result[-1][1]!=new[1]:
result.append(new)
j+=1
else: # Condition 3
h1=left[i][1]
h2=right[j][1]
new=[right[j][0],max(h1,h2)]
if result==[] or result[-1][1]!=new[1]:
result.append([right[j][0],max(h1,h2)])
i+=1
j+=1
while i<len(left): # Condition 4
if result==[] or result[-1][1]!=left[i][1]:
result.append(left[i][:])
i+=1
while j<len(right): # Condition 5
if result==[] or result[-1][1]!=right[j][1]:
result.append(right[j][:])
j+=1
return result
The basic idea is to divide and conquer the problem. In a basis case, where we only have one building, we return the building’s left up corner and its right down corner. (line 8-9). The crux of this problem is the `merge` function. It will always merge two sets of skyline points so that a set of merged valid skyline points is returned. So the `getSkyline` function is always merging two sets of already valid skyline points.
In `merge`, no matter how you append a skyline point to `result`, you always compare two things: 1. whether `result` is empty, which means you can always safely add it as a first element to `result`. 2. otherwise, whether the last element in `result` has the same height as the current skyline point that is about to be appended. That is because we want to avoid two consecutive skyline points on the same height.
In another perspective, `merge` always scans a pair of sets of skyline points from left to right, and only add those which:
- if the pair of sets both have skyline points left to be scanned, then the current skyline point will be added either if it has a higher height than the previous added skyline point from the other set, or the current result is empty.
- if one set has no skyline point left to be scanned, then we will add all the remaining skyline points to the result, as long as they don’t have the same height as the element added most recently.
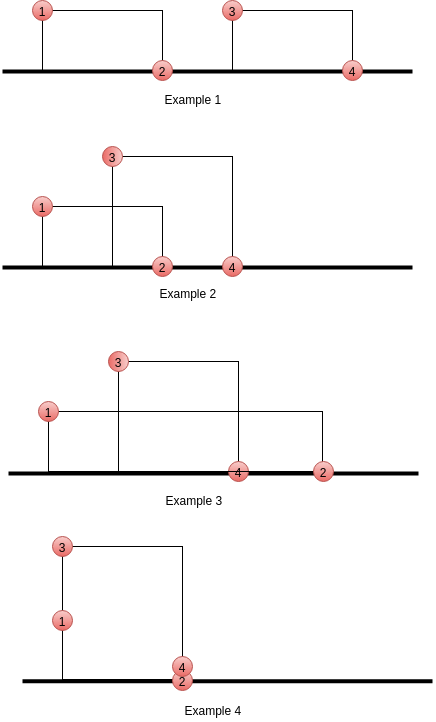
Let’s look at four simple examples. All the four examples have input of two buildings.
Example 1:
In `merge`, the `left` list has point 1 and 2. The `right` list has point 3 and 4. Point 1 will be scanned first and be added according to condition 1. Next, point 2 will be scanned and be added according to condition 1. After that, point 3 and point 4 will be added according to condition 5.
Example 2:
In `merge`, the `left` list has point 1 and 2. The `right` list has point 3 and 4. Point 1 will be scanned first and be added according to condition 1. Point 3 will be scanned next and be added according to condition 2. Point 2 will be scanned next but be discarded by condition 1’s sub-condition `result[-1][1]!=new[1]`. Point 4 will be added according to condition 5.
Example 3:
In `merge`, the `left` list has point 1 and 2. The `right` list has point 3 and 4. Point 1 will be scanned first and be added according to condition 1. Point 3 will be scanned next and be added according to condition 2. Point 4 will be scanned but be discarded by condition 2’s sub-condition `result[-1][1]!=new[1]`. Point 2 will be scanned at last and be added according to condition 4.
Example 4:
In `merge`, the `left` list has point 1 and 2. The `right` list has point 3 and 4. Point 1 and point 3 will be scanned together according to condition 3 and point 3 will be added to the result. Then, point 2 and point 4 will be scanned together according to condition 3 and point 2 (or point 4) will be added to the result.