I’ve been scratching my head for a day (06/24/2015) but it ended up that I am still baffled by the concept of Factor Analysis. So first of all, let me list what I’ve learned so far today.
PCA and Factor Analysis can be deemed similar from the perspective that they are both dimension reduction technologies. I’ve talked about PCA in an old post. But it can’t be emphasized more on how mistakenly people understand and use PCA. Several good questions about PCA have been raised: Apply PCA on covariance matrix or correlation matrix?. More on here and here.
By far the most sensible writing about Factor Analysis is from wikipedia: https://en.wikipedia.org/wiki/Factor_analysis. Remember the following expressions behind Factor Analysis:
There has been a debate over differences between PCA and Factor Analysis for a long time. My own point is that the objective functions they try to optimize are different. Now let’s discuss an example case within a specific context. Suppose, we have a normalized data set $latex Z_{p \times n}$. ($latex n$ is the number of data points. $latex p$ is the number of features.) The loading and latent factor scores of Factor Analysis on $latex Z_{p \times n}$ are $latex L_{p \times k}$ and $latex F_{k \times n}$. ($latex k$ is the number of latent factors.) Error Term is $latex \epsilon_{p \times n}$. $latex Cov(\epsilon) = Cov(\epsilon_1, \epsilon_2, \cdots, \epsilon_p)=Diag(\Psi_1, \Psi_2, \cdots, \Psi_p) = \Psi$. ($latex \epsilon_i$ is row vector of $latex \epsilon_{p \times n}$, indicating error of each feature is independently distributed. ) Hence we have: 
Then,
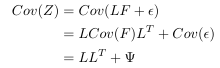Here we use a property $latex Cov(F)=I$ because that’s our assumption on Factor Analysis that latent factor scores should be uncorrelated and normalized.
Now on the same data set $latex Z_{p \times n}$ we apply PCA. PCA aims to find a linear transformation $latex P_{k \times p}$ so that $latex PZ=Y$ where $latex Cov(Y)$ should be a diagonal matrix. But there is no requirement that $latex Cov(Y)=I$. Let’s say there exists a matrix $latex Q$ s.t. $QP=I$. Then we have:
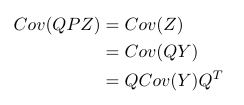But don’t forget that in PCA we impose $latex PP^T=I$. So actually $latex Q=P^T$. In other words, $latex Cov(Z)=P^TCov(Y)P$.
In the comparison above, we can see only when $latex Cov(Y) \approx I$ in PCA and $latex \Psi \approx 0$ in FA the loading of PCA and FA can be similar. Therefore I don’t agree with the post here: http://stats.stackexchange.com/questions/123063/is-there-any-good-reason-to-use-pca-instead-of-efa/123136#123136
P.S. the solution of $latex L$ and $latex F$ of either FA or PCA is not unique. Taking FA for example, if you have already found such $latex L$ and $latex F$ and you have an orthogonal matrix $latex Q$ s.t. $latex QQ^T = I$, then $latex Z=LF + \epsilon = LQQ^TF + \epsilon = (LQ)(Q^TF) + \epsilon = L’F’ + \epsilon$. Or you can always set $latex L’ = -L$ and $latex F’ = -F$ so that $latex Z=LF+\epsilon = (-L)\cdot(-F)+\epsilon$. This formula is intuitive, since it says that we can always find a set of opposite factors and assign negative weights of loadings to depict the same data.