I’ve talked about the vanishing gradient problem in one old post in normal multiple layer neural networks. Pascanur et al. (the first in References below) particularly discussed the vanishing gradient problem as well as another type of gradient instable issue, the exploding gradient problem in the scope of recurrent neural network.
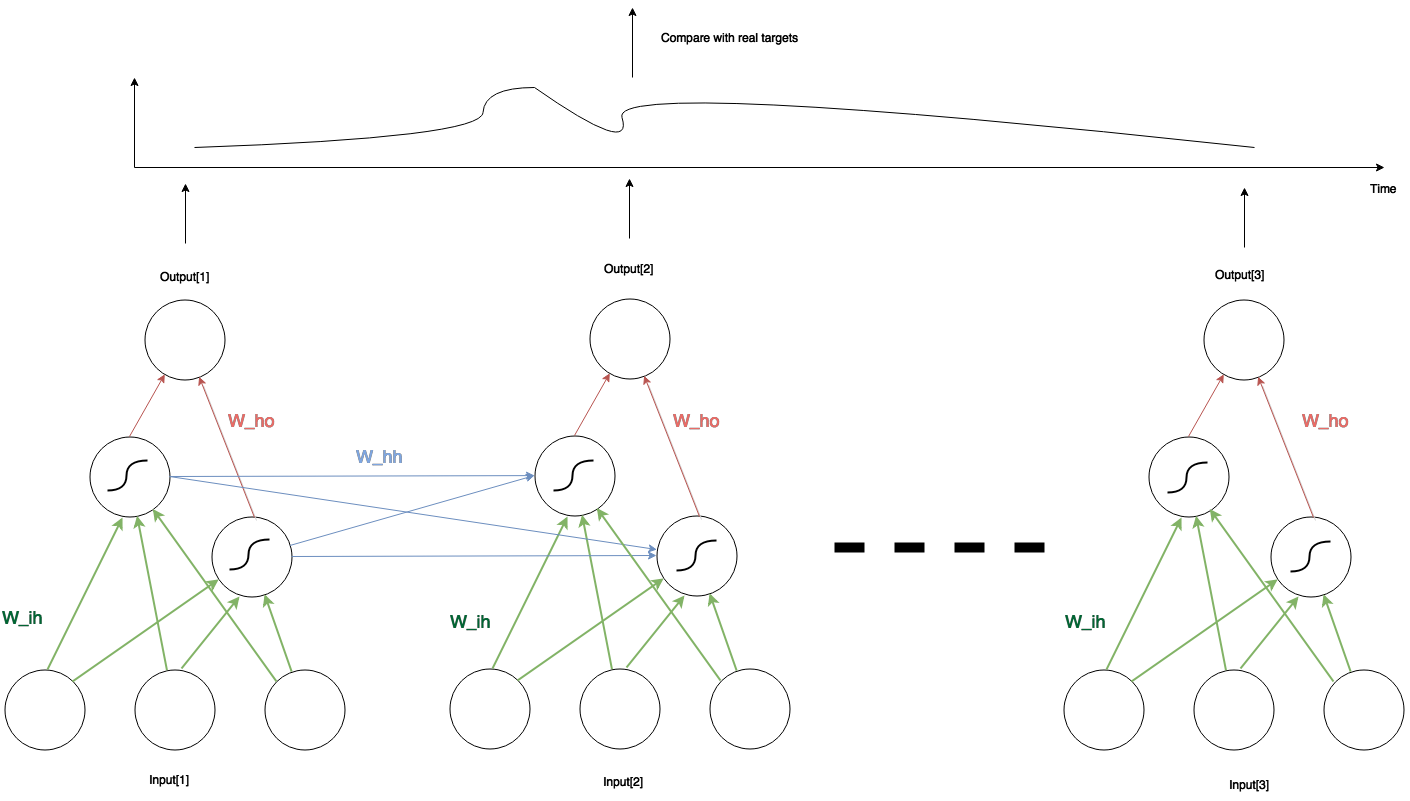
Let’s recap the basic idea of RNN. Here is the sketch of a simple RNN with three inputs, two hidden units and one output. In any given time, the network structure is the same: three input units connect to two hidden units through $latex W_{ih}$ (green lines in the pic), whereas the two hidden units connect to one output through $latex W_{ho}$ (red lines). Between two adjacent time steps, the two hidden units from the earlier network also connect to the two in the later network through $latex W_{hh}$ (blue lines). The two hidden units also perform an activation function. In our case we set the activation function to the sigmoid function. However, the outputs are just linear combination of the hidden unit values.
Pascanur pointed out that, if the weights $latex W_{hh}$ has no singular value larger than the largest possible value of the differentiation of the activation function of the hidden unit (in our case the sigmoid’s largest differentiation is 0.25), then the RNN suffers from the vanishing gradient problem (i.e., the much more earlier inputs tend to barely have influence on the later outputs). On the other hand, the largest singular value of $latex W_{hh}$ being larger than 0.25 is a necessary condition of the exploding gradient problem: the error of the output regarding the earlier input may augment to a exploding level so that the training never converges.
Purely by my curiosity, I did some experiments trying to replicate the vanishing gradient problem and the exploding gradient problem. Here are my steps:
- Initialize an RNN with three inputs, two hidden units and an output unit. The weights connecting them are crafted to let $latex W_{hh}$ have singular values tending to cause either the vanishing gradient problem or the exploding gradient problem. I will record the values of $latex W_{ih}$, $latex W_{hh}$ and $latex W_{ho}$.
- Randomly generate input sequences and feed into the RNN in step 1. Record the outputs of the inputs passing through the RNN. The inputs are generated in several sets. Each set has 500 input sequences. But different sets have different lengths of sequences. Doing so lets me examine how the vanishing (exploding) gradient problem forms regarding to the length of sequences.
- Now start to train a new RNN, with the input and output in step 2.
- Compare the weights from the two RNNs and see the training is successful (i.e. the weights are close)
Bear in mind that the largest singular value of $latex W_{hh}$ being larger than 0.25 is just a necessary condition of the exploding gradient problem. But I still keep going to see what will happen. The tables below contain the costs after certain epochs given certain lengths of sequences.
| epoch\seq length | 2 | 10 | 100 |
| 500 | 1.2e-5 | 1.44e-5 | 1.35e-5 |
| 1500 | 3.21e-9 | 5.11e-9 | 2.7e-9 |
When
| epoch\seq length | 2 | 10 | 100 |
| 500 | 0.00144 | 0.00358 | 0.0045 |
| 1500 | 2.39e-5 | 0.00352 | 0.0045 |
From the results above, I find that the vanishing gradient problem is hard to replicate (all the costs in the first table converged to small values), as opposed to the exploding gradient problem which emerged given sequences of length 100 (as you can see the costs stuck at 0.0045).
Code
rnn_generator.py: used to generate simulated input and output data passing by fixed weights
import numpy as np
import theano
import theano.tensor as tt
class RNNGenerator(object):
'''
Generate a simulated RNN with a fixed set of weights,
based on a fixed seed: np.random.seed(19910715)
Also check out RNNGenerator1, which generates simulated
RNN sequences of output with a fixed delay w.r.t input.
'''
def __init__(self, input_num, output_num, hidden_num):
np.random.seed(19910715)
self.input_num = input_num
self.output_num = output_num
self.hidden_num = hidden_num
# Initialize weights
self.W_hh = np.random.randn(hidden_num, hidden_num)
u, s, v = np.linalg.svd(self.W_hh, full_matrices=True, compute_uv=True)
s = np.diag(s)
print u, "\n\n", s, "\n\n", v, "\n"
print "Close?", np.allclose(self.W_hh, np.dot(np.dot(u, s), v)), "\n"
# Manually craft the largest singular value of W_hh as you wish
# s[0,0] = 10
# self.W_hh = np.dot(np.dot(u, s), v)
self.b_hh = np.random.randn(hidden_num)
self.W_hi = np.random.randn(hidden_num, input_num)
self.W_yh = np.random.randn(output_num, hidden_num)
self.b_yh = np.random.randn(output_num)
self.u, self.s, self.v = u, s, v
# Initialize output function
# Create symbols
self.W_hh_sym = theano.shared(self.W_hh)
self.W_hi_sym = theano.shared(self.W_hi) # hidden_num x input_num
self.b_hh_sym = theano.shared(self.b_hh)
inputs_sym = tt.matrix("inputs_sym") # data_num x input_num
# fn: a lambda expression to define a recurrent process
# sequences (if any), prior result(s) (if needed), non-sequences (if any)
outputs_sym, _ = theano.scan(fn=lambda inputs, prior_hidden, W_hh, W_hi, b_hh:
tt.nnet.sigmoid(tt.dot(W_hh, prior_hidden) + tt.dot(W_hi, inputs) + b_hh),
sequences=inputs_sym,
non_sequences=[self.W_hh_sym, self.W_hi_sym, self.b_hh_sym],
# outputs_info is the initial state of prior_hidden
outputs_info=tt.zeros_like(self.b_hh_sym))
# Doesn't need to update any shared variables, so set updates to None
self.output_func = theano.function(inputs=[inputs_sym], outputs=outputs_sym, updates=None)
def weights(self):
return self.W_hh, self.W_hi, self.W_yh, self.b_hh, self.b_yh
def inputs_outputs(self, data_num, seq_len):
m_inputs = np.random.randn(data_num, seq_len, self.input_num)
m_final_outputs = np.zeros((data_num, seq_len, self.output_num))
for j in xrange(data_num):
m_hidden = self.output_func(m_inputs[j, :, :])
m_outputs = np.zeros((seq_len, self.output_num))
for i in xrange(m_hidden.shape[0]):
m_outputs[i] = np.dot(self.W_yh, m_hidden[i]) + self.b_yh
m_final_outputs[j, :, :] = m_outputs
return m_inputs, m_final_outputs
if __name__ == '__main__':
input_num = 3
output_num = 1
hidden_num = 2
# How delayed outputs will rely on inputs
seq_len = 4
data_num = 3
rnn_generator = RNNGenerator(input_num, output_num, hidden_num)
W_hh, W_hi, W_yh, b_hh, b_yh = rnn_generator.weights()
print "Generated W_hh\n", W_hh, "\n"
print "Generated W_hi\n", W_hi, "\n"
print "Generated W_yh\n", W_yh, "\n"
print "Generated b_hh\n", b_hh, "\n"
print "Generated b_yh\n", b_yh, "\n"
m_inputs, m_outputs = rnn_generator.inputs_outputs(data_num, seq_len)
print "m_inputs\n", m_inputs, "\n"
print "m_outputs\n", m_outputs, "\n"
my_rnn.py: the main class of a simple rnn taking as input the simulated data
import theano
import theano.tensor as T
import numpy as np
import cPickle
import random
from rnn_generator import RNNGenerator
import time
np.random.seed(19910715)
class RNN(object):
def __init__(self, n_in, n_hidden, n_out, n_timestep):
rng = np.random.RandomState(1234)
self.activ = T.nnet.sigmoid
lr, momentum, input, target = T.scalar(), T.scalar(), T.matrix(), T.matrix()
self.W_uh = theano.shared(np.asarray(rng.normal(size=(n_in, n_hidden), scale=.01, loc=.0),
dtype=theano.config.floatX), 'W_uh')
self.W_hh = theano.shared(np.asarray(rng.normal(size=(n_hidden, n_hidden), scale=.01, loc=.0),
dtype=theano.config.floatX), 'W_hh')
self.W_hy = theano.shared(np.asarray(rng.normal(size=(n_hidden, n_out), scale=.01, loc=0.0),
dtype=theano.config.floatX), 'W_hy')
self.b_hh = theano.shared(np.zeros((n_hidden,), dtype=theano.config.floatX), 'b_hh')
self.b_hy = theano.shared(np.zeros((n_out,), dtype=theano.config.floatX), 'b_hy')
# Initialize the hidden unit state
h0_tm1 = theano.shared(np.zeros(n_hidden, dtype=theano.config.floatX))
# The parameter sequence fed into recurrent_fn:
# sequences (if any), outputs_info(s) (if needed), non-sequences (if any)
h, _ = theano.scan(self.recurrent_fn, sequences=input,
outputs_info=[h0_tm1],
non_sequences=[self.W_hh, self.W_uh, self.b_hh])
# y_pred is the predict value by the current model
y_pred = T.zeros((n_timestep, n_out))
# The cost is averaged over the number of output and the number of timestep
for i in xrange(n_timestep):
y_pred = T.set_subtensor(y_pred[i, :], T.dot(h[i], self.W_hy) + self.b_hy)
# You can determine whether to only compare the last timestep output
# or all outputs along all the timesteps
# cost = T.mean((target - y_pred)**2)
cost = T.mean((target[-1, :] - y_pred[-1, :])**2)
# This is the single output cost function from the original file
# cost = ((target - y_pred) ** 2).mean(axis=0).sum()
# Store previous gradients. Used for momentum calculation.
self.gW_uh = theano.shared(np.zeros((n_in, n_hidden)), 'gW_uh')
self.gW_hh = theano.shared(np.zeros((n_hidden, n_hidden)), 'gW_hh')
self.gW_hy = theano.shared(np.zeros((n_hidden, n_out)), 'gW_hy')
self.gb_hh = theano.shared(np.zeros((n_hidden)), 'gb_hh')
self.gb_hy = theano.shared(np.zeros((n_out)), 'gb_hy')
gW_uh, gW_hh, gW_hy, gb_hh, gb_hy = T.grad(
cost, [self.W_uh, self.W_hh, self.W_hy, self.b_hh, self.b_hy])
self.train_step = theano.function([input, target, lr, momentum], [cost, y_pred],
on_unused_input='warn',
updates=[(self.gW_hh, momentum * self.gW_hh - lr * gW_hh),
(self.gW_uh, momentum * self.gW_uh - lr * gW_uh),
(self.gW_hy, momentum * self.gW_hy - lr * gW_hy),
(self.gb_hh, momentum * self.gb_hh - lr * gb_hh),
(self.gb_hy, momentum * self.gb_hy - lr * gb_hy),
(self.W_hh, self.W_hh + self.gW_hh),
(self.W_uh, self.W_uh + self.gW_uh),
(self.W_hy, self.W_hy + self.gW_hy),
(self.b_hh, self.b_hh + self.gb_hh),
(self.b_hy, self.b_hy + self.gb_hy)],
allow_input_downcast=True)
# This part is for debugging.
# Create a function that takes the fixed weights from RNNGenerator as input and calculate output
W_uh, W_hh, W_hy, b_hh, b_hy = T.matrix("W_uh"), T.matrix("W_hh"),\
T.matrix('W_hy'), T.vector('b_hh'), T.vector('b_hy')
h_validated, _ = theano.scan(self.recurrent_fn, sequences=input, outputs_info=[h0_tm1],
non_sequences=[W_hh, W_uh, b_hh])
y_validated = T.zeros((n_timestep, n_out))
for i in xrange(n_timestep):
y_validated = T.set_subtensor(y_validated[i], T.dot(h_validated[i], W_hy) + b_hy)
self.output_validated_fn = theano.function([input, W_hh, W_uh, W_hy, b_hh, b_hy], y_validated,
updates=None, allow_input_downcast=True)
def recurrent_fn(self, u_t, h_tm1, W_hh, W_uh, b_hh):
h_t = self.activ(T.dot(h_tm1, W_hh) + T.dot(u_t, W_uh) + b_hh)
return h_t
def test_fixed_weights():
epoch = 1500
final_momentum = 0.9
initial_momentum = 0.5
momentum_switchover = 5
input_num = 3
output_num = 1
hidden_num = 2
seq_len = 2 # You can try different values of seq_len to check the cost
data_num = 500
rnn = RNN(input_num, hidden_num, output_num, seq_len)
lr = 0.001
rnn_generator = RNNGenerator(input_num, output_num, hidden_num)
W_hh, W_hi, W_yh, b_hh, b_yh = rnn_generator.weights()
m_inputs, m_outputs = rnn_generator.inputs_outputs(data_num, seq_len)
for e in xrange(epoch):
e_vals = []
for i in xrange(data_num):
u = m_inputs[i, :, :] # seq_len x input_num
t = m_outputs[i, :, :] # seq_len x output_num
mom = final_momentum if e > momentum_switchover \
else initial_momentum
cost, y_pred = rnn.train_step(u, t, lr, mom)
e_vals.append(cost)
# This part is for debugging
# Validate that using the fixed weights the output passing RNN
# is consistent with the generated output
# t_validated = rnn.output_validated_fn(u, W_hh.transpose(), W_hi.transpose(), W_yh.transpose(), b_hh, b_yh)
print "epoch {0}, average cost: {1}\n".format(e, np.average(e_vals))
print_result(rnn_generator, rnn, "my_rnn.log")
print "average error:{0}\n".format(np.average(e_vals))
def print_result(rnn_generator = None, rnn = None, filepath=None):
output_str = ""
if rnn_generator is not None:
W_hh, W_hi, W_yh, b_hh, b_yh = rnn_generator.weights()
output_str = output_str + "Generated W_hh\n" + str(W_hh) + "\n"
output_str = output_str + "Generated W_hi\n" + str(W_hi) + "\n"
output_str = output_str + "Generated W_yh\n" + str(W_yh) + "\n"
output_str = output_str + "Generated b_hh\n" + str(b_hh) + "\n"
output_str = output_str + "Generated b_yh\n" + str(b_yh) + "\n"
if rnn is not None:
output_str = output_str + "learnt W_hh\n" + str(rnn.W_hh.get_value()) + "\n"
output_str = output_str + "learnt W_uh\n" + str(rnn.W_uh.get_value()) + "\n"
output_str = output_str + "learnt W_hy\n" + str(rnn.W_hy.get_value()) + "\n"
output_str = output_str + "learnt b_hh\n" + str(rnn.b_hh.get_value()) + "\n"
output_str = output_str + "learnt b_hy\n" + str(rnn.b_hy.get_value()) + "\n"
print output_str
if filepath is not None:
with open(filepath, "w") as text_file:
text_file.write(output_str)
if __name__ == '__main__':
start_time = time.time()
test_fixed_weights()
end_time = time.time()
print "It took {0} seconds.".format((end_time - start_time))
References
Pascanur et al. paper (On the difficulty of training recurrent neural networks):
http://jmlr.org/proceedings/papers/v28/pascanu13.pdf
theano tutorial: http://deeplearning.net/tutorial/lstm.html
Recurrent neural network (The format is not very crystal clear to understand): https://www.pdx.edu/sites/www.pdx.edu.sysc/files/Jaeger_TrainingRNNsTutorial.2005.pdf
RNN as a generative model: http://karpathy.github.io/2015/05/21/rnn-effectiveness/?utm_content=bufferab271&utm_medium=social&utm_source=twitter.com&utm_campaign=buffer
A simple version of RNN I: http://www.nehalemlabs.net/prototype/blog/2013/10/10/implementing-a-recurrent-neural-network-in-python/
A simple version of RNN II: https://github.com/gwtaylor/theano-rnn