Background
This post reviews how we update weights using the back propagation approach in a neural network. The goal of the review is to illustrate a notorious phenomenon in training MLNN, called “gradient vanish”.
Start
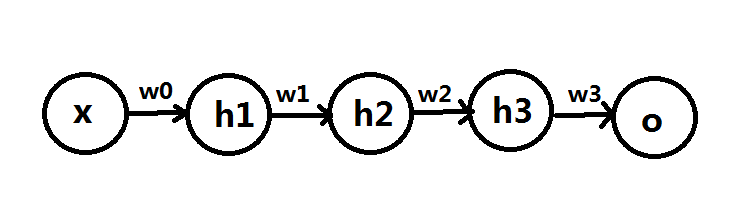
Let’s suppose that we have a very simple NN structure, with only one unit in each hidden layer, input layer and output layer. Each unit has sigmoid function as its activation function:
Also suppose we have training data: $latex (x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)$. Therefore, we have $latex h_1 = \frac{1}{1+e^{-w_0x_i}}$, $latex h_2 = \frac{1}{1+e^{-w_1h_1}}$, $latex h_3 = \frac{1}{1+e^{-w_2h_2}} $, $latex o = \frac{1}{1+e^{-w_3h_3}}$
Our cost function, which we want to minimize, is as follows:
$latex C=\sum\limits_{i=1}^n \left\Vert y_i – o_i\right\Vert^2$
If we are going to update $latex w_0$ after a round of inputting all the training data, we use the following rule (with $latex \epsilon$ as the learning rate):
$latex w_0 – \epsilon\nabla_{w_0}C$.
Due to the chain rule of derivatives, we can have equivalently:
$latex \nabla_{w_0}C = \sum\limits_{i=1}^n\frac{\partial C_x}{\partial o} \cdot \frac{\partial o}{\partial h_3} \cdot \frac{\partial h_3}{\partial h_2} \cdot \frac{\partial h_2}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_0}&s=3$
$latex =\sum\limits_{i=1}^n2(y_i – o_i) \cdot \delta'(w_3h_3) \cdot (-w_3) \delta'(w_2h_2) \cdot(-w_2) \cdot \delta'(w_1h_1) \cdot (-w_1) \cdot \delta'(w_0x_i) \cdot (-x_i)$
$latex =\sum\limits_{i=1}^n2(y_i – o_i)\cdot (-w_3) \cdot (-w_2) \cdot (-w_1) \cdot (-w_0) \cdot (-x_i) \cdot \delta'(w_3h_3) \cdot\delta'(w_2h_2) \cdot\delta'(w_1h_1)\cdot \delta'(w_0x_i)$
,where $latex \delta'(t) = (\frac{1}{1+e^{-t}})’$ is the derivative of sigmoid function.
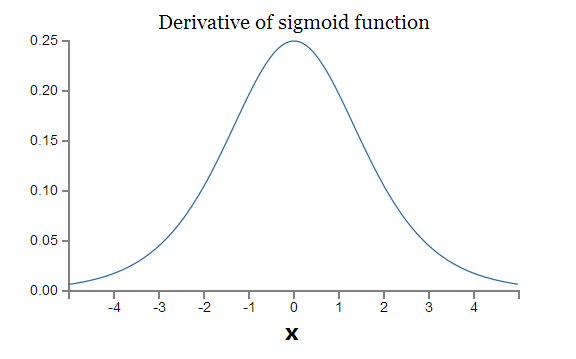
We should be very familiar with the shape of sigmoid function as well as its derivative.
From the two plots above, we know that the largest derivative of sigmoid function is 0.25 and it takes place at x=0. Let’s go back to $latex \nabla_{w_0}C$ of the multiple-layer neural network, which is the gradient descent of the weight associated with the layer farthest away from the output unit. It has four sigmoid derivatives, namely $latex \delta'(w_3h_3) \cdot\delta'(w_2h_2) \cdot\delta'(w_1h_1)\cdot \delta'(w_0x_i)$, each of which cannot overseed 0.25. As a result, $latex \nabla_{w_0}C$ would become very tiny.
That’s how gradient vanishing happens! It’s the phenomenon that certain weights in a multi-layer neural network cannot get updated effectively.
Reference