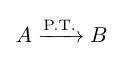Maybe it sounds simple to computer scientists, I just want to backup some logical deduction of myself in NP-completeness proofs in case I will deal with such proofs in the future.
In NP-completeness proof, we always want to find a polynomial-time reduction (transformation) from problem A to problem B, denoted as:
We say that there is an algorithm which for each instance $latex I$ of Problem A constructs Problem B in time which is polynomial with respect to the input size.
If $latex B \in P$, then $latex A \in P$. Think about it in contradiction: if $latex A$ is a NP-complete problem, a problem as hard as the “hardest problems” in the world, and suddenly we have a polynomial-time to transform it to problem B which is in P, then why not applying such transformation then solving B, both in polynomial time, every time we are given to solve $latex A$?
However, it is easy (and wrong) to think that if $latex B \in \text{NP-complete}$ then $latex A \in \text{NP-complete}$. It is wrong because I can even transform $\latex A$, a problem in P, by my will to any problem as tricky as NP-complete problems. So having $latex B \in \text{NP-complete}$ and a polynomial time transformation from $latex A$ to $latex B$ can’t guarantee $latex A$ to be anything.
If $latex A \in \text{NP-complete}$, then $latex B \in \text{NP-complete}$. Initially I think this is counter-intuitive. After all, by definition of polynomial time reduction, every instance of $latex A$ is mapped to $latex B$, but not every instance of $latex B$ can be assured to be mapped. Thinking in the following way makes me more sense: at least some instances of $latex B$ are mapped from every instance of $latex A$. So the mapped instances of $latex B$ are as hard as NP-complete problems. If the other instances of $latex B$ can be solved in P, problem $latex B$ itself still falls in the $latex NP-complete$ category.
All in all, I think all my logical deduction holds if the following diagram is true:
Otherwise, all the NP-complete proofs in this world will need to take with a grain of salt.