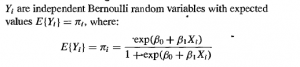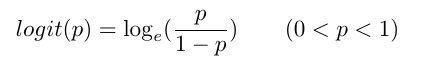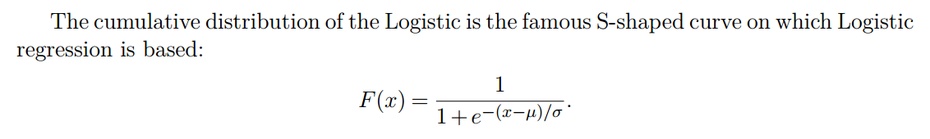背景
Logistic Regression是ML中再熟悉不过的Model了,它能基于数据X,得出生成binary label的概率:
(在上式中,X仅有一个feature)
假设你出生在Logistic Regression被发明之前且在Normal Linear Regression被发明之后,现在让你设计一个Model来预测Binary的label——Y,使得这个Model能够基于观测数据X得出Y。你会怎么设计呢?
(注:接下来我们都假设X仅有一个feature)
过程
- 你现在只知道Normal Linear Regression Model,所以你首先想尝试用Normal Linear Regression来fit数据X和label Y。这里label Y是binary的value。但是问题来了,Normal Linear Regression是基于很多假设的:
Error Term是Normal Distributed。显然在我们这个例子里,因为label Y是binary的value的,error term的value也是binary的,所以error term并不是normally distributed。
Constant Error Variance (也不符合,见之后的英文解释)
Normal Linear Regression并没有限制Mean Response的取值在固定的范围内。而我们现在却希望0<=E(Y)<=1
下面是完整的英文解释(转自KNNL):
题外话,一张不错的Normal Linear Regression的plot:
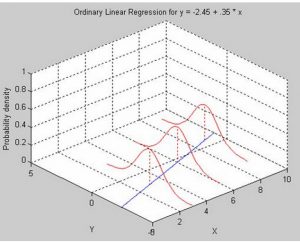
- Y是binary的,而Y=1的概率是连续的(在0到1之间)。既然不能直接用Normal Linear Regression来fit Y,那不如试试用X来fit Y=1的概率。至少,我们现在response variable是连续的了。
所以我们的脑海中,大概觉得这个Model要有这样的曲线 (转自http://cvxopt.org/_images/fig-7-1.png):
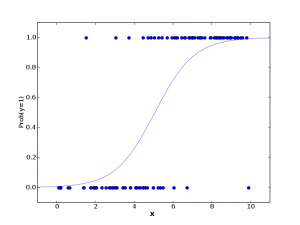
上图中,X(一个feature)作为横坐标。Y的取值为0或1。{X,Y}数据点为图中的蓝色散点。但是我们想象Y=1其实是有一定的概率的,随着X的增大,Y=1的概率不断增大,这个概率就对应了图中的曲线。当然这时候我们还是不能直接用Normal Linear Regression来fit Y=1的概率,因为这个概率的范围也只能在[0,1]中,而Linear Regression并没有这样的限制。
- 那么如果我们能把P(Y=1)通过一个function map到一个没有大小限制的取值范围内呢?如果能让P(Y=1)映射到一个连续的,大小无限制的范围内,我们不就可以用linear regression了吗?这时候,我们发现有一个function可以达到我们的目的。这就是logit function:
上式中,p=P(Y=1)。下面是logit function的图形,它将[0,1]之间的数值映射到了(-\infinity, +\infinity):
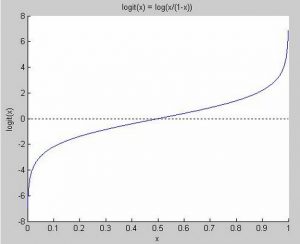
我们可以看到,当x轴的值大于0.5时,logit(x)大于0。而当x轴的值小于0.5时,logit(x)小于0。
- 好的,现在我们就用B0 + BX这条直线来fit logit(p)吧。对于某个数据点X,p对应的是Y=1的概率。虽然我们不知道p确切是多少,但是我们可以将logit(p)表示为:
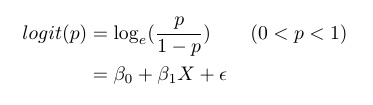
如果\epsilon是Normally Distributed with mean = 0, std = \sigma, 那么我们就用我们最熟悉的Normal Linear Regression来fit logit(p):
上式得到的Model又称为Probit Regression
如果\epsilon是Logistic Distributed with mean=0 and std = \sigma,我们得到:
这里我们得到的Model便是Logistic Regression的。倒数第三个等式到倒数第二个等式,我们用到了Logistic distribution的性质(截图自某课件):
——————————————————————————-
update 2018.5.17
5. after knowing $latex P(y=1|x)$, we can proceed to write the loss function for learning. The loss function for learning a binary predictor is usually cross-entropy:
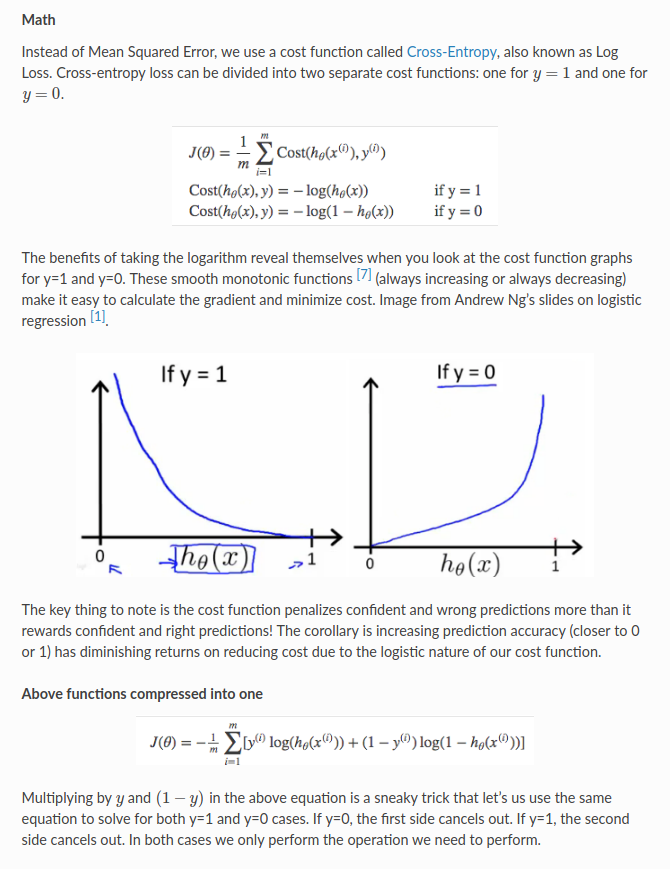
(In the above $latex h_\theta(x) = P(y=1|x)$, text from http://ml-cheatsheet.readthedocs.io/en/latest/logistic_regression.html)
Since $latex P(y=1|x)$ is differently formulated in probit and logit models, the weights eventually learned will be a little different. So probit and logit models share the same loss function but differ in the formulation of $latex P(y=1|x)$. This is the take-away of this post.
——————————————————————————-
6. 既然我们可以假设error term (\epsilon)为normally distributed或是logistic distributed,那么我们该如何选择什么时候用Probit Regression,什么时候用Logistic Regression呢?
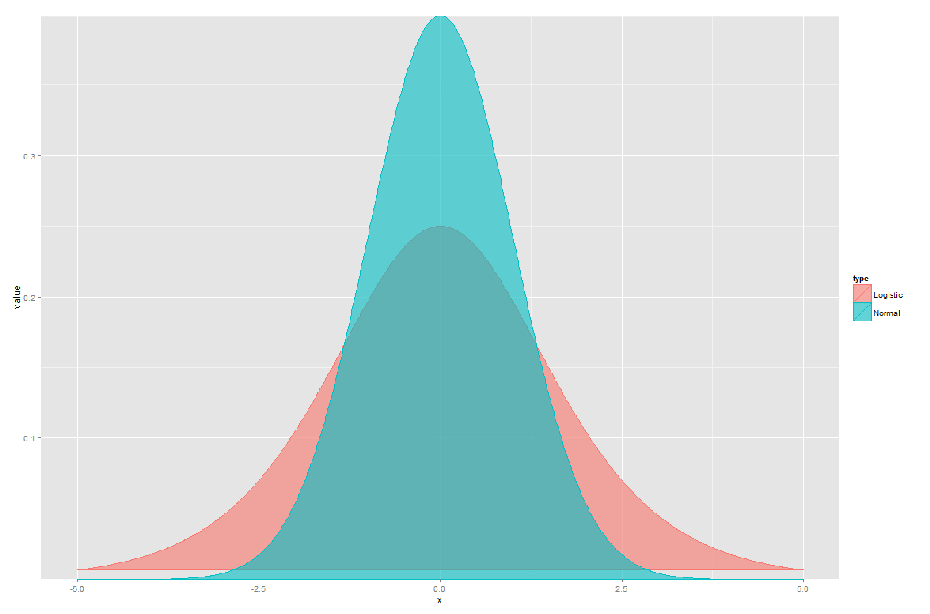
我们先来对比一下在mean = 0, std = 1的时候,normal distribution和logistic distribution的形状:
可以说,Logistic Distribution除了在中部矮了点,尾部平了点,其他和Normal Distribution别无区别。这么看来假定error term是logistic distributed或是normally distributed都没有太大的区别。那么,用Logistic Distribution的优势在于:
- P(Y=1)可以用closed form表达,即P(Y=1)由linear combination, exp, 除法等已知函数组成。若假定error term为normally distributed,P(Y=1)仅仅是normal distribution的cumulative distribution function (CDF),无法用其他函数表达。
- 因为P(Y=1)可以用closed form表达,Logistic Regression的结果就可易于解读。最常见的一个指标就是odds ratio。
我们讨论的logit function被称为link function——将X与Y的取值联系起来,虽然在原始的数据中Y的取值有种种的限制。在Normal Linear Regression的情况下,这个link function就是identity function。我们可能都听说过,Logistic Regression和Probit Regression都属于Generalized Linear Model。讲完本帖中的这么多,我们或许就清楚了Generalized Linear Model到底有哪些要素了:
- structural component, X和\beta的线性组合
- link function, 在我们的例子中,logit(p)就是link function。
- response distribution (Logistic regression或是 Probit regression中,logit(p)即是response distribution)
——————————————————————————-
update 2018.5.17
Now that we know different assumptions of the errors (either following normal distribution or logistic distribution) make probit and logit models different, we want to revisit the assumption of the errors in linear regression. Specifically, why does normal linear regression assume that the errors are normally distributed?
It turns out that solving weights in linear regression does not need the normal distribution assumption: you can obtain the best weights for the mean least square (MSE) loss function. The problem is that, are the weights calculated by MSE optimal in some sense? In fact, only when we assume the errors are normally distributed are the MSE estimators optimal for “maximum likelihood” or “unbiased of minimum variance”.
See good explanations:
——————————————————————————-